4.4 Algorithms for working with the table

The table makes it possible to develop a software bus or a universal program in the sense indicated by mathematics, that is, it allows you to encode and decode the numbers of algorithms that can be written and valid in the SDL language. This gives great advantages and, in particular, the fact that the execution of a given algorithm is not programmed, but encoded and entered as data for a table processing program. Therefore, their execution does not need to be recorded in the operators of the programming language in which the program of work with the table is executed. It has other advantages already mentioned that are provided by the program bus.

The correspondence table contains transitions recorded in the form of numbers. The algorithm for working with the table is that two tasks are performed.

1. For a given INPUT-CONDITION pair, find the required line in the correspondence table.
2. Perform actions in the order specified in the line, and in accordance with the content of the number set in it.

These algorithms are fairly simple and are not listed below. It can only be noted that the desire to optimize the volume of tables and write them in memory can complicate these algorithms.

Multitasking

A feature of telecommunications device software is the need for multitasking. Even with decentralized control, one processor performs several tasks alternately, that is, there are several processes in the PBX control device. Another feature - the start time of these tasks is unpredictable and depends on external causes. This problem is solved by the following method used for systems with multitasking processing. For each process, which is generally referred to as "call processing", a memory area is allocated. In each of the areas recorded global call status. It does not depend on the stage at which the call is located and which is indicated, as we have seen, by the local state, and reflects only the processing steps. It can take the following values: "free", "work", "waiting", "blocking".

The status "free" is assigned if the area is not occupied by the call.

State "work" - during the process.

The state of "waiting" marks the expectation of an external signal.

Fig. 4.5. Sequence of global call state values

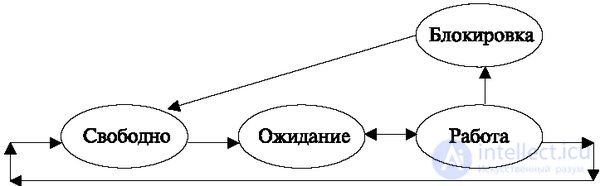
The status "blocking" marks emergency processes.

The system works by changing states in the order shown in Fig. 4.5.

1. Phase input. At this stage, a survey of external objects is carried out (see the scanning algorithm). When a signal is received, the INPUT from the external environment or another signal is recorded in special memory areas, called process memory areas, into which this signal is recorded ³ . In this phase, the global "free" state (more precisely, the absence of a record in the "state" area) is replaced by the global "waiting" state and transferred to the execution queue.
2. Phase performance. When referring to the queue of memory areas of processes waiting for service, the processor selects one of them. Then the process memory area is assigned a global "work" state. The processing of the input signal, as already discussed earlier, consists in performing a transition in accordance with the value of the incoming input signal and the local call state, the call processing step. This refers to local states, such as "dialing", "waiting for a release".

This pair is used to process the string with a table algorithm and assign it a local state at the end of the work. After that, the action is suspended in anticipation of a new input signal.

If these actions are successfully completed, the call is assigned a "waiting" state again (in Figure 4.5, the possibility of a return is indicated by a two-way arrow), and it returns to the queue of waiting processes. If this transition was final for the process (for example, “disconnecting”), then the memory area is freed and assigned the value “free”.

In case of abnormal termination, for example, if there is a signal that the transition time was exceeded, or another emergency timer, the process is switched to the "blocked" state. When the system is restored, the memory area of ​​the process, as a rule, is released and is assigned the state "free".

According to the considered order, call processing actions can be represented as work with three queues (Fig. 4.6).

This figure conditionally shows the processing order of memory areas organized in the form of queues.

The queue of free processes is a reserve of all free memory areas that can be used for "spawned" processes. The rest correspond to the definitions of the phases.

The queue of processes that are waiting for a signal is the memory areas that performed the actions, set the next state and are awaiting the introduction of a new INPUT signal.

The queue of processes waiting to be processed is the memory areas into which the input signal is recorded, and they are awaiting the processing procedure of the string of the table algorithm.

The call handling procedure is as follows. When an input signal arrives, the input manager, which is the scanning program, distributes it into one of two queues.

Fig. 4.6. Multitasking process and queue interaction

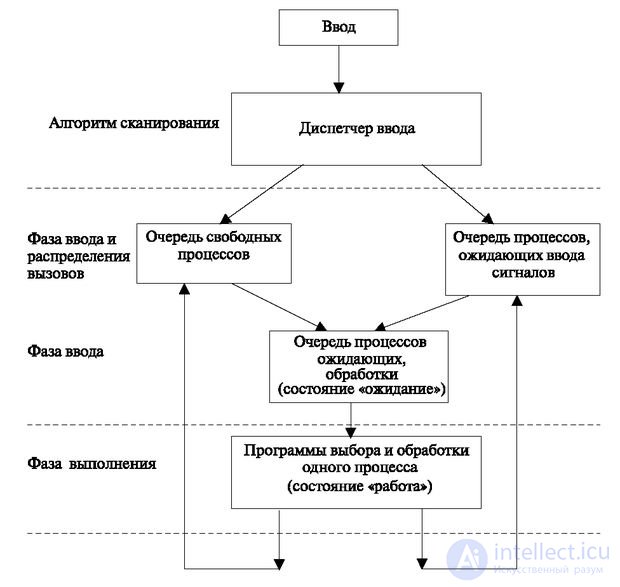
If this is the primary signal, then one of the memory areas of the processes in the queue of free processes is engaged, the “waiting” state is set instead of the “free” state and the process is transferred to the queue of processes waiting to be processed.

If this process already exists, which is determined by the application for scanning (see "Algorithms of individual functions performed in program-controlled stations" - "Scanning Algorithms"), after recording the incoming input signal, the process is transferred to the queue of processes waiting to be processed. It records the "waiting" state.

After the process is selected from the queue, the programs for selecting and processing one process are executed (the "work" state is recorded). In case of successful completion of processing, the process can be placed in a waiting queue with the installation of an application for scanning the next input signal or in a queue of free processes (at the end of the service).

Basic operations of working with the queue

For installation in a queue, removal, transfer to another queue, standard procedures for working with a list are used [3]. In this case, you can apply operations with lists or with a special type of list - a queue. A queue is a list in which elements are added from one (end of the queue), and deleted from the other end (the beginning of the queue), which somewhat simplifies the algorithms for working with them.

The following operations are used to work with lists:

• INSERT IN THE LIST,
• REMOVE FROM THE LIST,
• TRANSFER FROM THE LIST ... .. TO THE LIST ...,
• TO FIND.....

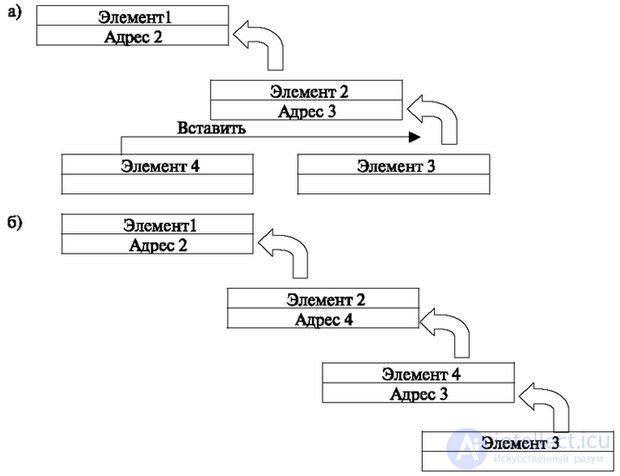
For installation in the list, the INSERT TO LIST procedure shown in Fig. 2 is used. 4.7.

In fig. 4.7a shows the implementation of the list. The field "element" contains information about the object recorded in the list. The field "address" allows you to carry out operations with the elements of the list. Each previous element contains a link (address) to the next. It also shows the need to insert a fourth element between the second and third. The location is arbitrary, and, as we will see, the procedure is the same for all places and does not depend on the length of the list.

In fig. 4.7b shows a new list with the fourth element inserted. On the initial data containing the address of the previous element (element 3) and the number of the new (element 4), it took two actions:

• change the field ("address") of the previous element in the queue (this is element 2);
• in the new element (element 4) assign a number to the cell “address” - the address of the link of the previous element. It is equal to the address of the element, which will now follow the new element (link to the element with address 3).

Fig. 4.7. The principle of installation in the list a) Source list; b) List, after the operation "paste"

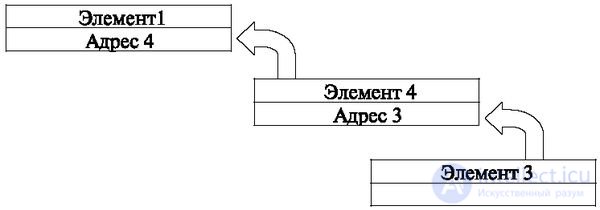
The REMOVE operation consists in assigning the address of a link to the previous element address of the link of the element being deleted. Example of operation DELETE - element 2 from the queue shown in fig. 4.8. This process is shown in Fig. 4.7. In the example, the link address of the element to be deleted 2 is assigned to the link address of the element 1 in front of it.

Transferring a call from one list to another contains both operations (DELETE - INSERT).

As already mentioned, the queue is a special kind of list. Work with queue is characterized by the chosen discipline of service queue. The simplest and most massive discipline is “first in, first out”.

With this strategy, the elements of the list are numbered according to the order in which they are received. The first incoming call at the beginning of the queue receives the number 1, the last at the end receives the number in accordance with the queue length.

Fig. 4.8. The principle of removal from the list

For the convenience of working with the queue, two pointers are introduced:

  BEGINNING OF QUEUE
 END OF QUEUE 

In order to INSERT a new item in the queue, you need to increase the END LIST pointer by 1 (END QUEUE: = END QUEUE + 1) and INSERT it into the LIST with the resulting END QUEUE. Then the new item will be inserted at the end of the queue with the next number.

In order to DELETE THE ELEMENT (to take it into processing), it is necessary to increase the START OF QUEUE index by 1 (START QUEUE: = START QUEUE +1). Then, the next item will be the first (move to the top of the queue).

The difference between the numbers END OF THE QUEUE AND THE BEGINNING OF THE QUEUE shows the LENGTH of QUEUE.

Since the increase in numbers should not be infinite, then for a list of length l it is considered to be that the element following the element with the number (l - 1) has the number 0.