Tetration

In mathematics, tetration (or hyper-4) is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation ↑↑ and the left-exponent xb are common.

tetration 5^^5 online

Under the definition as repeated exponentiation, means , where n copies of a are iterated via exponentiation, right-to-left, i.e. the application of exponentiation n−1 times. n is called the "height" of the function, while a is called the "base," analogous to exponentiation. It would be read as "the nth tetration of a".

It is the next hyperoperation after exponentiation, but before pentation. The word was coined by Reuben Louis Goodstein from tetra- (four) and iteration.

Tetration is also defined recursively as

allowing for attempts to extend tetration to non-natural numbers such as real, complex, and ordinal numbers.

The two inverses of tetration are called super-root and super-logarithm, analogous to the nth root and the logarithmic functions. None of the three functions are elementary.

Tetration is used for the notation of very large numbers.

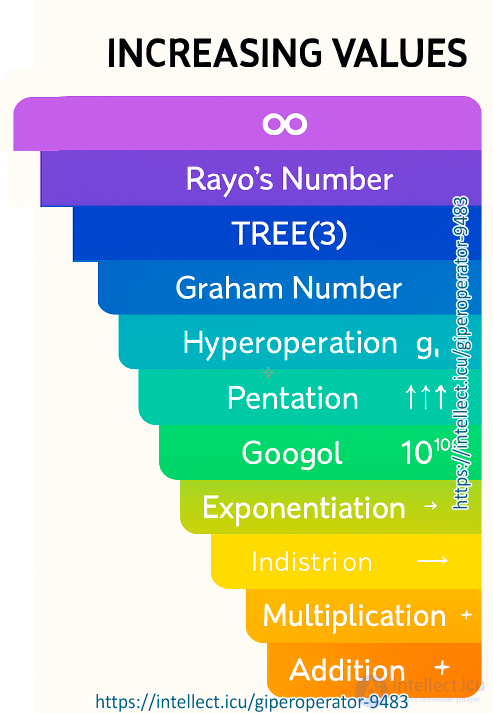
The first four hyperoperations are shown here, with tetration being considered the fourth in the series. The unary operation succession, defined as , is considered to be the zeroth operation.

1. Addition n copies of 1 added to a combined by succession.
2. Multiplication n copies of a combined by addition.
3. Exponentiationa n copies of a combined by multiplication.
4. Tetrationna= n copies of a combined by exponentiation, right-to-left.

Importantly, nested exponents are interpreted from the top down: ⁠abc⁠ means ⁠a(bc)⁠ and not ⁠(ab)c.⁠

Succession, , is the most basic operation; while addition (a+n) is a primary operation, for addition of natural numbers it can be thought of as a chained succession of n successors of a; multiplication (a×n) is also a primary operation, though for natural numbers it can analogously be thought of as a chained addition involving n numbers of a. Exponentiation can be thought of as a chained multiplication involving n numbers of a and tetration (na) as a chained power involving n numbers a. Each of the operations above are defined by iterating the previous one;[1] however, unlike the operations before it, tetration is not an elementary function.

The parameter a is referred to as the base, while the parameter n may be referred to as the height. In the original definition of tetration, the height parameter must be a natural number; for instance, it would be illogical to say "three raised to itself negative five times" or "four raised to itself one half of a time." However, just as addition, multiplication, and exponentiation can be defined in ways that allow for extensions to real and complex numbers, several attempts have been made to generalize tetration to negative numbers, real numbers, and complex numbers. One such way for doing so is using a recursive definition for tetration; for any positive real a>0 and non-negative integer n≥0, we can define na recursively as:[1]

The recursive definition is equivalent to repeated exponentiation for natural heights; however, this definition allows for extensions to the other heights such as 0a, −1a, and ia as well – many of these extensions are areas of active research.

There are many terms for tetration, each of which has some logic behind it, but some have not become commonly used for one reason or another. Here is a comparison of each term with its rationale and counter-rationale.

• The term tetration, introduced by Goodstein in his 1947 paper Transfinite Ordinals in Recursive Number Theory[2] (generalizing the recursive base-representation used in Goodstein's theorem to use higher operations), has gained dominance. It was also popularized in Rudy Rucker's Infinity and the Mind.
• The term superexponentiation was published by Bromer in his paper Superexponentiation in 1987.[3] It was used earlier by Ed Nelson in his book Predicative Arithmetic, Princeton University Press, 1986.
• The term hyperpower[4] is a natural combination of hyper and power, which aptly describes tetration. The problem lies in the meaning of hyper with respect to the hyperoperation sequence. When considering hyperoperations, the term hyper refers to all ranks, and the term super refers to rank 4, or tetration. So under these considerations hyperpower is misleading, since it is only referring to tetration.
• The term power tower[5] is occasionally used, in the form "the power tower of order n" for . Exponentiation is easily misconstrued: note that the operation of raising to a power is right-associative (see below). Tetration is iterated exponentiation (call this right-associative operation ^), starting from the top right side of the expression with an instance a^a (call this value c). Exponentiating the next leftward a (call this the 'next base' b), is to work leftward after obtaining the new value b^c. Working to the left, use the next a to the left, as the base b, and evaluate the new b^c. 'Descend down the tower' in turn, with the new value for c on the next downward step.

Owing in part to some shared terminology and similar notational symbolism, tetration is often confused with closely related functions and expressions. Here are a few related terms:

Terms related to tetration

Terminology	Form
Tetration
Iterated exponentials
Nested exponentials (also towers)
Infinite exponentials (also towers)

In the first two expressions a is the base, and the number of times a appears is the height (add one for x). In the third expression, n is the height, but each of the bases is different.

Care must be taken when referring to iterated exponentials, as it is common to call expressions of this form iterated exponentiation, which is ambiguous, as this can either mean iterated powers or iterated exponentials.

There are many different notation styles that can be used to express tetration. Some notations can also be used to describe other hyperoperations, while some are limited to tetration and have no immediate extension.

Notation styles for tetration

Name	Form	Description
Rudy Rucker notation	na	Used by Maurer [1901] and Goodstein [1947]; Rudy Rucker's book Infinity and the Mind popularized the notation.[nb 1]
Knuth's up-arrow notation		Allows extension by putting more arrows, or, even more powerfully, an indexed arrow.
Conway chained arrow notation		Allows extension by increasing the number 2 (equivalent with the extensions above), but also, even more powerfully, by extending the chain.
Ackermann function		Allows the special case a=2 to be written in terms of the Ackermann function.
Iterated exponential notation		Allows simple extension to iterated exponentials from initial values other than 1.
Hooshmand notations[6]	uxpa⁡nan	Used by M. H. Hooshmand [2006].
Hyperoperation notations		Allows extension by increasing the number 4; this gives the family of hyperoperations.
Double caret notation	a^^n	Since the up-arrow is used identically to the caret (^), tetration may be written as (^^); convenient for ASCII.

One notation above uses iterated exponential notation; this is defined in general as follows:

with n as.

There are not as many notations for iterated exponentials, but here are a few:

Notation styles for iterated exponentials

Name	Form	Description
Standard notation		Euler coined the notation , and iteration notation fn(x) has been around about as long.
Knuth's up-arrow notation		Allows for super-powers and super-exponential function by increasing the number of arrows; used in the article on large numbers.
Text notation	exp_a^n(x)	Based on standard notation; convenient for ASCII.
J Notation	x^^:(n-1)x	Repeats the exponentiation. See J (programming language)[7]
Infinity barrier notation		Jonathan Bowers coined this,[8] and it can be extended to higher hyper-operations

Because of the extremely fast growth of tetration, most values in the following table are too large to write in scientific notation. In these cases, iterated exponential notation is used to express them in base 10. The values containing a decimal point are approximate.

Examples of tetration

x	2x	3x	4x	5x	6x	7x
1	1	1	1	1	1	1
2	4 (22)	16 (24)	65,536 (216)	2.00353 × 1019,728	exp103⁡(4.29508)	exp104⁡(4.29508) (10106.03123×1019,727)
3	27 (33)	7,625,597,484,987 (327)	)	exp104⁡(1.09902)		)
4	256 (44)	1.34078 × 10154 (4256)	exp103⁡(2.18726)	exp104⁡(2.18726)	exp105⁡(2.18726)	exp106⁡(2.18726)
5	3,125 (55)	1.91101 × 102,184 (53,125)	exp103⁡(3.33928) (101.33574×102,184)		exp105⁡(3.33928)	exp106⁡(3.33928)
6	46,656 (66)	2.65912 × 1036,305 (646,656)	exp103⁡(4.55997) (102.0692×1036,305)	exp104⁡(4.55997)	exp105⁡(4.55997)	7)
7	823,543 (77)	3.75982 × 10695,974 (7823,543)	exp103⁡(5.84259) (3.17742 × 10695,974 digits)	exp104⁡(5.84259)	exp105⁡(5.84259)	exp106⁡(5.84259)
8	16,777,216 (88)	6.01452 × 1015,151,335	exp103⁡(7.18045) (5.43165 × 1015,151,335 digits)	exp104⁡(7.18045)	exp105⁡(7.18045)	exp106⁡(7.18045)
9	387,420,489 (99)	4.28125 × 10369,693,099	exp103⁡(8.56784) (4.08535 × 10369,693,099 digits)	exp104⁡(8.56784)	exp105⁡(8.56784)	exp106⁡(8.56784)
10	10,000,000,000 (1010)	1010,000,000,000	exp103⁡(10) (1010,000,000,000 + 1 digits)	exp104⁡(10)	exp105⁡(10)	exp106⁡(10)

Remark: If x does not differ from 10 by orders of magnitude, then for all . For example, m=4 in the above table, and the difference is even smaller for the following rows.

Tetration of the imaginary unit or complex numbers.

This is a complex and still open question in mathematics.

Tetration for the imaginary unit i — or, more generally, tetration for non-integer powers and complex numbers —

does not have a generally accepted simple answer in the same sense that i²= −1.

Tetration (superpower, hyperoperator-4) — This is iterative exponentiation.

Denoted as na and defined recursively:

For example:

• i^^1 = i

• i^^2 = i ⁱ

• i^^3 = i ⁽ⁱⁱ⁾

• i^^4 = i^(i(ii))

Calculating the first tetrations ni

To find specific tetration values ​​for i, you need to calculate degree i with a complex exponent:

i^^2 = iⁱ

To calculate iⁱ , we use the formula for the complex exponent b^^a = e^blna.

1. Find the natural logarithm ln(i):

   i = e^iπ/2​
   ln i = i π​/2

   (Principal value)

2. Substitute iⁱ into the formula:

   i^^2 = iⁱ = e^i⋅lni = e^{i⋅(iπ/2​)} = e^i2π/2 ​= e^−π/2​ ≈ 0.207879576...

Tetration can be extended in two different ways; in the equation na, both the base a and the height n can be generalized using the definition and properties of tetration. Although the base and the height can be extended beyond the non-negative integers to different domains, including n0, complex functions such as ni, and heights of infinite n, the more limited properties of tetration reduce the ability to extend tetration.

Pentation

In mathematics, pentation (or hyper-5) is the fifth hyperoperation. Pentation is defined to be repeated tetration, similarly to how tetration is repeated exponentiation, exponentiation is repeated multiplication, and multiplication is repeated addition. The concept of "pentation" was named by English mathematician Reuben Goodstein in 1947, when he came up with the naming scheme for hyperoperations.

The number a pentated to the number b is defined as a tetrated to itself b - 1 times. This may variously be denoted as , , , , or ba, depending on one's choice of notation.

For example, 2 pentated to the 2 is 2 tetrated to the 2, or 2 raised to the power of 2, which is 22=4. As another example, 2 pentated to the 3 is 2 tetrated to the result of 2 tetrated to the 2. Since 2 tetrated to the 2 is 4, 2 pentated to the 3 is 2 tetrated to the 4, which is .

Based on this definition, pentation is only defined when a and b are both positive integers.

Pentation is the next hyperoperation (infinite sequence of arithmetic operations) after tetration and before hexation. It is defined as iterated (repeated) tetration (assuming right-associativity). This is similar to as tetration is iterated right-associative exponentiation.[1] It is a binary operation defined with two numbers a and b, where a is tetrated to itself b − 1 times.

The type of hyperoperation is typically denoted by a number in brackets, []. For instance, using hyperoperation notation for pentation and tetration, means tetrating 2 to itself 2 times, or . This can then be reduced to .

The word "pentation" was coined by Reuben Goodstein in 1947 from the roots penta- (five) and iteration. It is part of his general naming scheme for hyperoperations.[2]

There is little consensus on the notation for pentation; as such, there are many different ways to write the operation. However, some are more used than others, and some have clear advantages or disadvantages compared to others.

• Pentation can be written as a hyperoperation as a[5]b. In this format, a[3]b may be interpreted as the result of repeatedly applying the function x↦a[2]x, for b repetitions, starting from the number 1. Analogously, a[4]b, tetration, represents the value obtained by repeatedly applying the function x↦a[3]x, for b repetitions, starting from the number 1, and the pentation a[5]b represents the value obtained by repeatedly applying the function x↦a[4]x, for b repetitions, starting from the number 1.[3][4] This will be the notation used in the rest of the article.

• In Knuth's up-arrow notation, a[5]b is represented as a↑↑↑b or a↑3b. In this notation, a↑b represents the exponentiation function ab and a↑↑b represents tetration. The operation can be easily adapted for hexation by adding another arrow.
• In Conway chained arrow notation, a[5]b=a→b→3.[5]
• Another proposed notation is ba, though this is not extensible to higher hyperoperations.[6]

The values of the pentation function may also be obtained from the values in the fourth row of the table of values of a variant of the Ackermann function: if A(n,m) is defined by the Ackermann recurrence A(m−1,A(m,n−1)) with the initial conditions A(1,n)=an , then a .[7]

As tetration, its base operation, has not been extended to non-integer heights, pentation a[5]b is currently only defined for integer values of a and b where a > 0 and b ≥ −2, and a few other integer values which may be uniquely defined. As with all hyperoperations of order 3 (exponentiation) and higher, pentation has the following trivial cases (identities) which holds for all values of a and b within its domain:

• 
• 

Additionally, we can also introduce the following defining relations:

• 
• 
• 
• 
• 

Other than the trivial cases shown above, pentation generates extremely large numbers very quickly. As a result, there are only a few non-trivial cases that produce numbers that can be written in conventional notation, which are all listed below.

Some of these numbers are written in power tower notation due to their extreme size. Note that .

• 
• 
• .
• 
• 
• (a power tower of height 7,625,597,484,987) ≈exp107,625,597,484,986⁡(1.09902)
• (a power tower of height 3[4]7,625,597,484,987) ≈exp103[4]7,625,597,484,987−1⁡(1.09902)
• (a number with over 10153 digits)
• (a number with more than 10102184 digits)

tetration 5^^5 online

Applications Tetration and Pentation
The practical application of Tetration and Pentation is limited to specific areas, as operations above exponentiation (e.g., tetration and pentation) quickly produce very large numbers that are difficult to process. However, Tetration and Pentation can be useful in some scientific and engineering fields:

1. Computational Theory and Algorithm Complexity
Tetration and Pentation can be used to analyze algorithms with very high computational complexity. For example, some problems in theoretical computer science, such as computing large numbers or constructing computational circuits, require operations that can be described using Tetration and Pentation .

2. Cryptography
Cryptography uses large numbers to create complex keys and ciphers. Exponentiation and other Tetration and Pentation can play a role in creating more complex encryption schemes and data security methods. 3. Astronomy and Physics
In models that require working with very large numbers (for example, estimates of the size of the universe or the lifetimes of objects), Tetration and Pentation can be useful for conveniently representing such numbers.

4. Theoretical Mathematics
In mathematics, Tetration and Pentation (hyperoperators) are used in the study of large numbers, such as Graham's number, which is related to the Ramsey conjecture. This number is too large to be written using ordinary powers, and hyperoperators allow us to describe it.

5. Number Theory and Combinatorics
In the field of number theory, especially when dealing with rapidly growing sequences, Tetration and Pentation can be used to describe such functions and their properties.

Despite limited direct application in everyday computing, Tetration and Pentation play an important role in theoretical research and in solving problems involving extremely large numbers.

See also

• Tetration and Pentation Operations, Superroot, and Applications
• Hyperoperator and Hyperoperation - definition, inverse operations and applications