Lecture
Teaching without a teacher (English Unsupervised learning , self-study , spontaneous learning ) is one of the methods of machine learning, in solving which the test system spontaneously learns to perform the task, without interference from the experimenter. From the point of view of cybernetics, is one of the types of cybernetic experiment. As a rule, it is suitable only for tasks in which descriptions of a set of objects are known (training sample), and it is required to detect internal interrelations, dependencies, regularities existing between objects.
Learning without a teacher is often contrasted to learning with a teacher, when for each learning object the “right answer” is forcibly given, and it is required to find a relationship between stimuli and system responses.
Despite numerous applied advances, teaching with the teacher was criticized for its biological improbability. It is difficult to imagine a learning mechanism in the brain that would compare the desired and actual output values, performing a correction using feedback. If we allow a similar mechanism in the brain, then where do the desired outputs come from? Teaching without a teacher is a much more plausible model of learning in a biological system. Developed by Kohonen and many others, it does not need a target vector for exits and, therefore, does not require comparison with predefined ideal answers [1] .
To build a theory and move away from a cybernetic experiment in various theories, one tries to formalize a learning experiment without a teacher mathematically. There are many different subtypes of the formulation and definition of this formalization. One of which is reflected in pattern recognition theory.
Such a departure from the experiment and the construction of the theory are associated with different opinions of specialists in their views. Differences, in particular, consist in answering the question: “Are uniform principles possible to adequately describe images of different nature, or is such a description a task for specialists of specific knowledge each time?”.
In the first case, the statement should be aimed at identifying general principles for the use of a priori information in the preparation of an adequate description of images. It is important that here a priori information about the images of different nature is different, and the principle of taking them into account is the same. In the second case, the problem of obtaining a description is taken out of the general setting, and the theory of learning pattern recognition machines from the point of view of the statistical theory of pattern recognition learning can be reduced to the problem of minimizing the average risk in a special class of decision rules [2] .
In the theory of pattern recognition, there are basically three approaches to this problem [3] :
An unsupervised experimental training scheme is often used in the theory of pattern recognition and machine learning. At the same time, depending on the approach, it is formalized into one or another mathematical concept. And only in the theory of artificial neural networks the problem is solved experimentally, applying one or another type of neural networks. At the same time, as a rule, the resulting model may not have an interpretation, which is sometimes referred to as minus neural networks. But nevertheless, the results are no worse, and, if desired, can be interpreted by applying special methods.
Main article: Cluster analysis
Learning experiment without a teacher in solving the problem of pattern recognition can be formulated as a task of cluster analysis. A sample of objects is divided into disjoint subsets, called clusters, so that each cluster consists of similar objects, and the objects of different clusters are significantly different. Baseline information is presented as a matrix of distances.
Solution methods
Clustering can play a supporting role in solving problems of classification and regression. To do this, you first need to split the sample into clusters, then apply some very simple method to each cluster, for example, to bring the target dependence to a constant.
Solution methods
Main article: Generalization of concepts
As in the case of distinction experiments, which can be mathematically formulated as clustering, when generalizing concepts, one can investigate a spontaneous generalization , in which similarity criteria are not introduced from the outside or are not imposed by the experimenter.
At the same time, in the experiment on “pure generalization” a model of the brain or perceptron is required to switch from a selective response to one stimulus (say, a square in the left side of the retina) to a similar stimulus that does not activate any of the same sensory endings (square on the right side of the retina). The generalization of a weaker species includes, for example, the requirement that the system’s reactions extend to elements of a class of such stimuli that are not necessarily separated from the stimulus already shown (or heard, or perceived by touch).
The task of reducing the size of the source information is presented in the form of characteristic descriptions. The task is to find such sets of features, and such meanings of these features, which are most often (not accidentally often) found in the feature descriptions of objects.
Baseline information is presented in the form of feature descriptions, and the number of features can be quite large. The task is to present this data in a space of lower dimension, if possible, minimizing the loss of information.
Solution methods
Some methods of clustering and reduction of dimension build representations of the sample in a space of dimension two. This allows you to display multidimensional data in the form of flat graphs and analyze them visually, which contributes to a better understanding of the data and the very essence of the problem being solved.
Solution methods
Alfa-reinforcement system - a reinforcement system in which the weight of all active bonds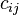 
that end in some element 
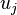vary by the same amount 
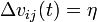, or at a constant speed during the whole time of reinforcement, and the weights of inactive bonds do not change during this time. A perceptron that uses an α-reinforcement system is called an α-perceptron. A reinforcement is called discrete if the magnitude of the change in weight is fixed, and continuous if this quantity can take an arbitrary value.
[
k-means ( k-means method ) is the most popular clustering method. It was invented in the 1950s by the mathematician Hugo Steinhaus [1] and almost simultaneously by Stuart Lloyd [2] . Special popularity gained after the work of McQueen [3] .
The algorithm is such that it seeks to minimize the total quadratic deviation of cluster points from the centers of these clusters:
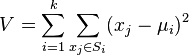
Where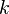 
- the number of clusters 
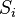- received clusters, 
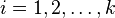and 
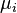- centers of mass of vectors 
.
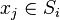By analogy with the principal component method, the cluster centers are also called principal points , and the method itself is called the principal point method [4] and is included in the general theory of principal objects that provide the best approximation of the data [5] .
The algorithm is a version of the EM algorithm, also used to separate a mixture of Gaussians. It splits the set of elements of a vector space into a previously known number of clusters k .
The basic idea is that at each iteration the center of mass is recalculated for each cluster obtained in the previous step, then the vectors are divided into clusters again according to which of the new centers was closer in the selected metric.
The algorithm ends when at some iteration there is no change in the center of mass of the clusters. This happens in a finite number of iterations, since the number of possible partitions of a finite set is finite, and at each step the total standard deviation V does not increase, so looping is impossible.
As David Arthur and Sergey Vasilvitsky showed, on some classes of sets the complexity of the algorithm in time required for convergence is equal to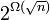 
. [6]
The action of the algorithm in the two-dimensional case. Starting points are randomly selected.
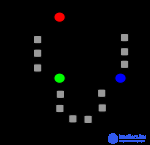
Starting points and randomly selected starting points. |
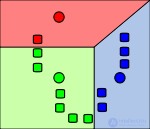
Points related to the initial centers. Splitting on the plane - Voronoi diagram relative to the initial centers. |
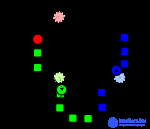
Calculation of new cluster centers (Looking for the center of mass). |
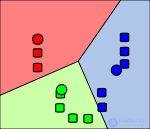
The previous steps are repeated until the algorithm converges. |
|---|
A typical example of the convergence of the method of k averages to a local minimum. In this example, the result of “clustering” by the k-means method contradicts the apparent cluster structure of the data set. Small circles indicate data points, four-star stars are centroids. The data points belonging to them are the same color. The illustration was prepared with the help of the Mirkes applet [7] .
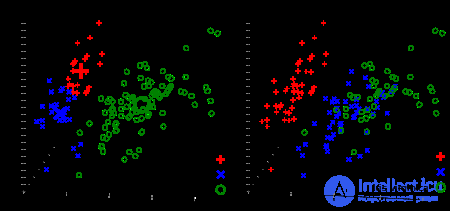
The result of clustering by the k- average method for Fisher irises and real types of irises visualized using ELKI. Cluster centers are marked with large, translucent markers.
The neural network implementation of K-means, a network of vector signal quantization (one of the versions of Kohonen's neural networks), is widely known and used.
There is an extension k-means ++, which is aimed at the optimal choice of the initial values of cluster centers.
Comments
To leave a comment
Machine learning
Terms: Machine learning