Resolution

It was shown above that all the rules of inference that have been considered so far are consistent, but the question of their completeness in relation to the algorithms of inference in which they are used has not yet been discussed. Search algorithms, such as iterative deepening, are complete in the sense that they allow to find any achievable goal, but if the available inference rules are inadequate, then the goal becomes unattainable; this means that there is no evidence in which only these inference rules could apply. For example, if we refuse to use the rule of removing a two-way implication, we will not be able to complete the proof set forth in the previous section. And in this section, the only rule of logical inference is presented, the resolution rule, which makes it possible to obtain an inference algorithm that becomes complete in conjunction with any complete search algorithm.

Let's start by using a simple version of the resolution rule in the vampus world. Consider the steps leading up in the figure, a: the agent returns from the square [2,1] to the square [1,1], and then goes to the square [1,2], where he feels an unpleasant smell, but does not feel the breeze. We introduce the following additional facts in the knowledge base:

R ₁₁ : ¬ B _1,2

R ₁₂ : B _1.2 <=> (P _1,1 v P _2,2 v P _1,3 )

Using the same process that led to the statement R ₁₀ given above, we can now conclude that there are no holes in the squares [2.2] and [1.3] (recall that with respect to the square [1.1] it is already known that it is not):

R ₁₃ : ¬ P _2.2

R ₁₄ : ¬ P _1,3

In addition, you can apply the rule of removing a two-sided implication to the statement R ₃ , and then apply the separation rule to the result obtained in combination with the statement R ₅ to find out that in at least one of the squares [1,1], [2] , 2] or [3.1] there is a pit:

R ₁₅ : P _1.1   v   P _2,2   v   P _3,1

It is here that conditions arise that allow for the first time to use the resolution rule (the elimination of contradiction rule): the ¬P _2.2 literal in the R ₁₃ statement, the opposite of the P _2.2 literal in the R ₁₅ statement, is eliminated, resulting in

to receive the following statement:

The corresponding line of reasoning can be expressed in words as follows: if there is a well in at least one of the squares [1,1], [2,2] or [3,1], but it is not in the square [2,2], then the well must be at least squared [1,1] or [3,1]. Similarly, the literal ¬P _{1.1 is} eliminated in the statement R ₁₆ opposite to the literal P _1.1 in the statement R ₁₆ , which results in the following statement:

R 17: R 3,1

The corresponding line of reasoning can be expressed in words as follows: if there is a well in at least one of the squares [1,1] or [3,1], but it is not in the square [1,1], then it is in the square [3, one]. These two final stages of inference are examples of the application of the rule of inference , called the rule of a single resolution :

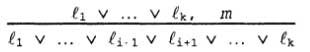
where each of the expressions l is a literal, and the expressions l _i and m are mutually inverse literals (that is, such literals that one of them is the negation of the other). Thus, an expression (disjunction of literals) and one more literal are taken in the rule of a single resolution, after which a new expression is formed. Note that this single literal can be considered a disjunction of one literal, also called a single expression . The rule of a single resolution can also be generalized to the rule of a full resolution :

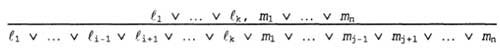
where l _i and m _j are mutually inverse literals. If we dealt only with expressions having length two, we could write this rule as follows:

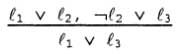
This means that two expressions are taken in the resolution rule and a new expression is generated containing all the literals of the two original expressions, with the exception of two mutually inverse literals. For example, the following logical conclusion can occur:

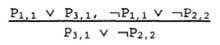
The process of applying the resolution rule is connected with the need to fulfill one more formal requirement: the resulting statement must contain only one copy of each literal11. The operation to remove additional copies of literals is called factorization . For example, after removing opposite literals in expressions (A v B) and (A v ¬ B), an expression (A vA) will be obtained, which should be reduced to A

The consistency of the resolution rule can be easily proved by considering the literal _i - If the literal l _i is true, then the literal lg is false, and therefore the expression m ₁ v ... v m _{j -1} v m _{j +1} v ... v m _n must be true, since that the expression m ₁ v ... v m _{n is} true. If the literal l _i is false, then the expression l ₁ v ... v l _{i -1} v l _{i -1} v ... v l _k must be true, since it is given that the expression _{l 1} v ... v l _{k is} true. Thus, the literal l _i is either true or false, so one or the second of these conclusions is valid, and this is precisely what is stated in the rule of the resolution.

An even more attractive feature of the resolution rule is that it forms the basis for a family of complete inference procedures. Any complete search algorithm in which only the resolution rule applies allows to derive any conclusion that follows from any knowledge base in propositional logic. Nevertheless, one warning must be made: the resolution rule is complete only in the narrow sense of the term. If it is known that Statement A is true, the resolution rule cannot be used to automatically form Corollary A v B. However, in this case the resolution rule can be used to find the answer to the question of whether the statement A v B. is true. This property of the resolution rule is called a complete refutation ( refutation completeness) means that the resolution rule can always be used either to confirm or to refute a statement, but it cannot be used to enumerate all true statements. The following two subsections describe how a resolution rule can be used to make a logical inference.