The basic idea in constructing logical models of knowledge is as follows - all information necessary for solving applied problems is considered as a set of facts and statements, which are represented as formulas in a certain logic. Knowledge is represented by a set of such formulas, and the acquisition of new knowledge is reduced to the implementation of inference procedures. The basis of logical models of knowledge is the concept of formal theory, defined by the card:
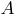 - A countable set of basic characters (alphabet);
- A countable set of basic characters (alphabet);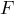 - set, called formulas;
- set, called formulas;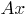 - a selected subset of a priori true formulas (axioms);
- a selected subset of a priori true formulas (axioms);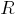 - a finite set of relationships between formulas, called inference rules.
- a finite set of relationships between formulas, called inference rules.
The main advantages of logical knowledge models:
- as a “foundation”, here we use the classical apparatus of mathematical logic, whose methods are well studied and formally substantiated;
- There are quite effective inference procedures, including those implemented in the Prolog programming language;
- knowledge bases can be stored only a lot of axioms, and all other knowledge can be obtained from them by the rules of inference.
In logical knowledge models, words describing entities of the subject domain are called terms (constants, variables, functions), and words describing relationships of entities are predicates.
Predicate - logical
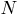
-Aarn propositional function, defined for the domain and taking values of either truth or falsity.
A propositional function is a function that assigns one of the truth values (“true”, “false”) to the objects in the domain of definition. The predicate takes the values "true" or "false" depending on the values of the terms included in it.
The method of describing the subject area used in logical models of knowledge leads to the loss of some nuances inherent in the natural perception of man, and therefore reduces the descriptive ability of such models.
Difficulties arise when describing "multi-sorted" worlds, when objects are not homogeneous. So, the statements:
"2 + 2 = 4"
"Moscow is the capital of Russia"
have the same meaning of "truth", but a different meaning. In order to overcome the difficulties and extend the descriptive capabilities of logical knowledge models, pseudo-physical logics, logic operating on fuzzy, empirical quantifiers, providing inductive (from particular to general), deductive (from general to specific) and traductive (at one level of generality) conclusions are developed. Such extended models, combining the capabilities of logical and linguistic approaches, are called logical-linguistic domain models.
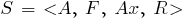
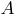 - A countable set of basic characters (alphabet);
- A countable set of basic characters (alphabet);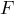 - set, called formulas;
- set, called formulas;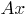 - a selected subset of a priori true formulas (axioms);
- a selected subset of a priori true formulas (axioms);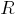 - a finite set of relationships between formulas, called inference rules.
- a finite set of relationships between formulas, called inference rules.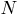 -Aarn propositional function, defined for the domain and taking values of either truth or falsity. A propositional function is a function that assigns one of the truth values (“true”, “false”) to the objects in the domain of definition. The predicate takes the values "true" or "false" depending on the values of the terms included in it.
-Aarn propositional function, defined for the domain and taking values of either truth or falsity. A propositional function is a function that assigns one of the truth values (“true”, “false”) to the objects in the domain of definition. The predicate takes the values "true" or "false" depending on the values of the terms included in it.
Comments
To leave a comment
Knowledge Representation Models
Terms: Knowledge Representation Models