Inference in a formal logical system is a procedure that, from a given group of expressions, derives a semantically correct expression that is different from the given group. This procedure, presented in a specific form, is the rule of inference. If the group of expressions that makes up the premise is true, then it must be guaranteed that the use of the inference rule will provide a true expression as a conclusion.
Two methods are most commonly used. The first is the method of inference rules or the method of natural (natural) inference, so named because the type of reasoning used in the predicate calculus approaches that of ordinary human reasoning. The second is the resolution method. It is based on the calculus of resolvents.
This article discusses the second method. Method resolutions proposed in 1930. in Herbrand’s doctoral dissertation for proving theorems in formal systems of the first order.
The resolution method is based on the calculus of resolvents. There is a theorem stating that the question of the provability of an arbitrary formula in the predicate calculus reduces to the question of the provability of the empty list in the calculus of resolvents. Therefore, the proof that the list of formulas in the calculus of resolvents is empty is equivalent to the proof of the falsity of a formula in the predicate calculus.
The idea of the resolution method is that the proof of the truth or falsity of the assumption, for example:
conducted by the method of the contrary. To this end, the original set of sentences includes the axioms of the formal system and the negation of the hypothesis being proved:
If in the process of proof there is a contradiction between the negation of the hypothesis and the axioms, which is expressed in finding an empty list (clause), then the hypothesis is correct.
Such proof can be obtained on the basis of the Herbrand theorem, which guarantees that the existing contradiction can always be achieved in a finite number of steps, whatever the truth values given to the functions present in the hypotheses and conclusions.
In the resolution method, a set of sentences is usually considered as a composite predicate containing several predicates connected by logical functions and quantifiers of existence and generality. Since predicates of the same meaning can have a different form, sentences are converted into a clausal form — a kind of conjunctive normal form (CNF), in which quantifiers of existence, universality, symbols of implication, equivalence, etc. are removed.
In the clausal form, the entire initial logical formula is represented as a set of sentences (clause)
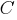
called
clausal set 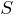
:
Any suggestion
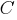
from which the clausal set is formed
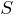
, is a set of atomic predicates or their negatives, connected by the disjunction symbol:
A predicate or its negation is called a disjunct , a literal, an atom, an atomic formula.
The essence of the resolution method is to verify whether or not it contains
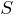
empty sentence
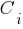
. Sentence
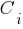
is empty if it does not contain any characters. Since the condition of truth
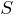
is the truth of all
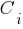
included in
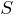
then the falsity of any
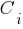
consisting in the fact that many
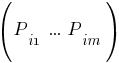
forming
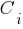
will be empty, indicating the falsity of the original logical formula.
If a
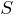
contains an empty sentence
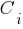
then
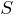
contradictory (impracticable). If the offer
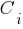
is not empty, then an attempt is made to output sentences
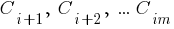
until an empty one is received (which will always be the case for an impracticable
).
For this, in two sentences, one of which consists of one letter, and the second contains an arbitrary number of letters, is a
counter pair of letters (for example
and
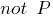
), which is deleted, and a new sentence is formed from the remaining parts (for example, from
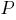
and
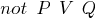
is displayed
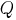
).
Sentence
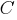
reformed from existing
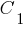
and
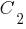
is called the
resolvent 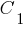
and
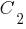
. For example:
If at the withdrawal of sentences two one-liter clauses are formed, which form a counter pair, then their resolvent will be an empty clause. Since the presence of an empty disjunct means that
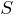
is false, then the impracticability of the original statement, formulated as a negation:
proves the truth of the assumption:
Since in the predicate logic in sentences, the presence of variables is allowed, in order to find contra pairs it is necessary to introduce a unification operation (substitution of a constant instead of a variable into predicates that have the same predicate symbols, but different letters). The unification algorithm was developed in 1966 by J. Pitra and, independently of him, J. Robinson: in order to unify two different expressions, the most common unifier is sought - LEU (a substitution in which an expression with greater descriptive power agrees with an expression that has a small descriptive power) . The presence of this algorithm made it possible to implement the method of Erbran’s resolutions in the form of a computer program.
So, if it is required by the resolution method to prove the truth of any logical statement, then the negation of this statement is transformed into a clausal form, according to its proposals, an empty sentence is searched using unification and derivation of resolvents. The impossibility of negation confirms the truth of the statement in question.
The resolution method is widespread due to the high efficiency of machining. Based on it, the Prolog language is built. However, a person does not use such logic in the process of reasoning, and this gives grounds for searching for more natural procedures for the human consciousness to draw conclusions.
A significant drawback of the resolution method is that it is intended only to prove theorems. It is not suitable for generating new offers. In addition, if the proposal is not a theorem, the resolution may lead to the construction of an infinite decision tree.
Example: solution output in a logical model based on the resolution method.
Statements are given:
- "Socrates is a man";
- “Man is a living being”;
- "All living things are mortal."
It is required by the method of resolutions to prove the statement "Socrates is mortal . "
Decision:
Step 1. We transform statements into a disjunctive form:
Step 2. Write down the negation of the target expression (the required output), i.e. Socrates is immortal:
Step 3. We put together a conjunction of all clauses (that is, build a QF), including the negation of the target expression:
Step 4. In the cycle, we perform an operation for searching resolvents on each pair of clauses:
Receiving an empty disjunct means that the phrase "Socrates is immortal" is false, it means that the saying "Socrates is mortal" is true.
In general, the resolution method is interesting because of its simplicity and systemic nature, but it is applicable only for a limited number of cases (the evidence should not have great depth, and the number of potential resolutions should not be large). In addition to the method of resolutions and rules of inference, there are other methods of obtaining conclusions in the logic of predicates.
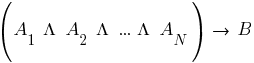
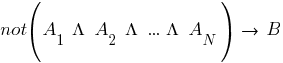
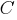 called clausal set
called clausal set 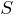 :
: 
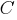 from which the clausal set is formed
from which the clausal set is formed 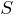 , is a set of atomic predicates or their negatives, connected by the disjunction symbol:
, is a set of atomic predicates or their negatives, connected by the disjunction symbol: 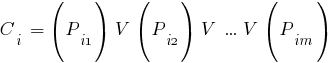
 empty sentence
empty sentence  . Sentence
. Sentence 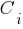 is empty if it does not contain any characters. Since the condition of truth
is empty if it does not contain any characters. Since the condition of truth 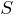 is the truth of all
is the truth of all 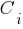 included in
included in 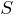 then the falsity of any
then the falsity of any 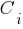 consisting in the fact that many
consisting in the fact that many 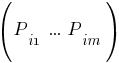 forming
forming 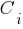 will be empty, indicating the falsity of the original logical formula.
will be empty, indicating the falsity of the original logical formula. 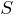 contains an empty sentence
contains an empty sentence 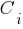 then
then 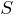 contradictory (impracticable). If the offer
contradictory (impracticable). If the offer 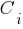 is not empty, then an attempt is made to output sentences
is not empty, then an attempt is made to output sentences 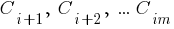 until an empty one is received (which will always be the case for an impracticable
until an empty one is received (which will always be the case for an impracticable 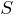 ).
). 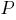 and
and 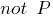 ), which is deleted, and a new sentence is formed from the remaining parts (for example, from
), which is deleted, and a new sentence is formed from the remaining parts (for example, from 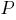 and
and 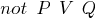 is displayed
is displayed 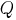 ).
). 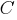 reformed from existing
reformed from existing 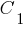 and
and 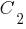 is called the resolvent
is called the resolvent 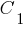 and
and 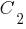 . For example:
. For example: 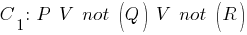
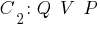
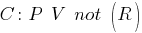
 is false, then the impracticability of the original statement, formulated as a negation:
is false, then the impracticability of the original statement, formulated as a negation: 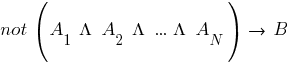
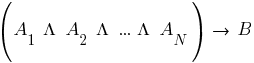


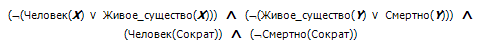

Comments
To leave a comment
Knowledge Representation Models
Terms: Knowledge Representation Models