Inference in a formal logical system is a procedure that, from a given group of expressions, derives a semantically correct expression that is different from the given group. This procedure, presented in a specific form, is the rule of inference. If the group of expressions that makes up the premise is true, then it must be guaranteed that the use of the inference rule will provide a true expression as a conclusion.
Two methods are most commonly used. The first is the rule of inference method, or the method of natural (natural) inference, so named because the type of reasoning used in the predicate calculus approaches that of ordinary human reasoning. The second is the resolution method. It is based on the calculus of resolvents.
This article discusses
the inference rule method . In predicate logic, the rule is used, which of the two expressions
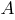
and
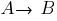
displays a new expression
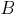
.
Different literature contains different names for the method of inference rules, for example, deductive inference rules or, more often, modus ponens . The principle of operation of inference rules is well illustrated by the following example:
“If it is known that the statement “ A ” entails (implies) the statement “ B ” , and also it is known that the statement “ A ”is true, then, therefore, “ B ”is true”
In predicate logic, there are universal rules that operate on formulas containing free variables. Solving problems (drawing conclusions) in logical models can be based on the application of similar rules to the original set of true predicates as evidence of the correctness of a composite predicate. Such a method of obtaining a solution is called non-axiomatic or in other words - natural, natural and coincides with the output methods in production models.
Since the answer is obtained as a conclusion from a combination of already existing logical formulas, by analogy with the conclusions in production models it can be called a direct (inverse) conclusion. However, it should always be borne in mind that in formal logic, cause-effect relationships are ignored.
The essence of the inference procedure is the recursive use of the substitution of known values in a composite predicate. In this case, it is guaranteed in principle that the proof of the truth of the result can be verified by a formal procedure.
If, in a formal logical model, the mechanism of logical inference uses the method of inference rules, that is, the basis of this model is attributed to productional or logical-linguistic.
Example: solution output in a logical model based on an inference rule - modus ponens.
Statements are given:
- "Socrates is a man";
- “Man is a living being”;
- "All living things are mortal."
Required to prove the statement "Socrates is mortal . "
Decision:
Step 1. Imagine the statements in predicate form:
Step 2. Based on the inference rule (modus ponens) and the substitution (Socrates / X) in the first predicate, we get the statement:
"Socrates is a living thing."
Step 3. Based on the inference rule (modus ponens) and the substitution (Socrates / Y) in the third predicate, we obtain the statement:
"Socrates is mortal"
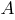 and
and 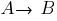 displays a new expression
displays a new expression 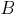 .
. 
Comments
To leave a comment
Knowledge Representation Models
Terms: Knowledge Representation Models