Lecture
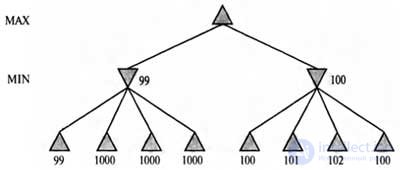 |
| A tree with two half moves, for which a minimax search may not be suitable |
The alpha-beta search still generates and evaluates a large and completely useless search tree. Of course, you can provide some kind of verification of this situation in this algorithm, but it will simply mask the main problem: many of the calculations performed in the alpha-beta algorithm do little to solve the problem. The situation in which there is only one valid move is not much different from the one where there are several valid moves, moreover, one of them is correct, and the others are clearly catastrophic.
In such a situation, having a “well-defined favorite” would be desirable to quickly reach a solution after conducting a small search volume, rather than wasting time that could be used more productively later, in a more problematic position. This leads to the idea of a node deployment utility.
A good search algorithm should choose options for the deployment of sites with high utility, i.e. those options that are likely to lead to the discovery of a much better move. If there are no deployment options for nodes whose utility exceeds their cost (measured in time-consuming), the algorithm should stop searching and select the course. It should be noted that such an improvement concerns not only situations with clear favorites, but also those cases when there are symmetric moves for which an arbitrarily large search volume does not allow showing that one move is better than another.
Arguments about which calculations should be performed, and which should not, are called meta- arguments (discourses on reasoning). This approach applies not only to the conduct of games, but in general to reasoning of any kind. All calculations are performed in order to develop the best solutions, they all have a cost and are characterized by a certain probability of achieving a specific improvement in the quality of the solution. Alpha-beta search is an implementation of the simplest form of meta-reasoning, namely, the theorem that some branches of a tree can be ignored without harming the whole game. But such meta reasoning can be done much better.
Finally, consider once again the nature of the search itself. Algorithms for heuristic search and gaming operate by generating sequences of specific states (starting from the initial state), and then using the evaluation function. Of course, people play games differently. In chess, the player is often guided by a specific goal (for example, to catch the opponent's queen) and can use this goal to selectively develop workable plans to achieve it. Sometimes this kind of approach based on reasoning, guided goal, or planning, allows you to completely eliminate the combinatorial search.
The David Wilkins Paradise program is the only program that successfully used goal-driven reasoning to play chess; she was able to solve some chess problems, for which combinations of 18 moves were required. Nevertheless, there is still no complete understanding of how to combine these two types of algorithms into a reliable and efficient system, although the Bridge Baron program can be considered as a step in the right direction.
A fully integrated system would be a significant achievement not only in the field of game research, but also for all research on artificial intelligence in general, since it would serve as a good basis for creating an intelligent general purpose agent.
Comments
To leave a comment
Knowledge Representation Models
Terms: Knowledge Representation Models