6. Standardization and testing of diagnostic models - Designing psychodiagnostic

Это продолжение увлекательной статьи про конструирование психодиагностических тестов.

...

пространстве общих факторов, полученных методами факторного анализа исходного пространства признаков. И в той и в другой работе важное, если не решающее, значение придается психологическому осмыслению выделяемых группировок испытуемых. Возможность четкой интерпретации полученных группировок как определенных психологических типов служит достаточно веским доводом в пользу не случайного разбиения испытуемых на группы, которое могло бы произойти под действием какого-либо иррелевантного решаемой диагностической задаче фактора (отсюда, собственно, и проистекает название «типологический подход»).

The quality assessment of the diagnostic model obtained as a result of applying the typological approach is usually carried out by comparing with the usual linear diagnostic model built without dividing the objects of the training sample into groups. For example, the following indicator is used.

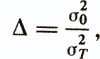
where σ20 is the residual variance of the usual linear regression model, and σ2T is calculated by the formula

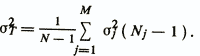
Here σ2j is the residual dispersion of the regression diagnostic model y j = y j ( x) for the group Gj, determined from the expression

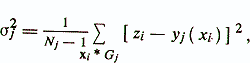
where N is the total number of subjects;
Nj - the number of subjects in the group Gj;
M is the number of groupings.

Also to test the hypothesis about the identity of a conventional linear regression model and a set of regression equations yj = yj (x), Fisher's F-criterion can be used / Eliseeva I. I. et al., 1977 /

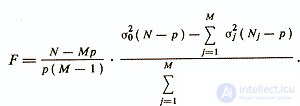
The effectiveness of a typological approach, for purely formal reasons, cannot be lower than the effectiveness of a conventional linear diagnostic model, which can be considered as a degenerate case of a piecewise linear model. At the same time, in addition to practical gain, the typological approach has a certain theoretical value - it reveals the relationship between the diagnosis of psychological features, as groups of characters, and psychological types, as groups of subjects. The ideal of the typological approach, notes B. V. Kulagin / 1984 /, is the development of such a method that will allow for each individual to choose the optimal diagnostic model.

6. Standardization and testing of diagnostic models

The test result of the test person xi, calculated using the diagnostic model yi = y ( xi), is usually called the initial test score or, often, the “raw” score. For a better understanding of this result, among other results, it is further artificially transformed based on an analysis of the empirical distribution of test scores in a representative sample of subjects. The procedure for such a transformation is called standardization .

There are three main types of standardization of primary test scores: 1) reduction to normal form; 2) reduction to standard form; 3) quantile standardization / Melnikov V. M et al., 1985 /.

Bringing the distribution of test scores to a normal form.

There are two main circumstances that explain the feasibility of artificially reducing the distribution of primary test scores to a normal form. Firstly, a significant part of the procedures of classical mathematical statistics was developed for random variables with Gaussian normal distribution. And, secondly, it makes it possible to describe diagnostic standards in a compact form.

To determine the method of conversion of y , histograms of the distribution of primary test estimates are usually considered. They allow you to identify left and right-sided asymmetry, positive or negative kurtosis and other deviations from normality. In psychological studies, logarithmic normal distributions of “raw” points are often encountered. In this case, the distribution of the distribution to the Gaussian form is achieved by logarithm y. On the contrary, trigonometric and power-law transformations of “raw” points are often used to normalize the distribution curves with a shallow left branch and a steep right one.

The use of computers allows you to automate the selection and fitting of the required conversion of primary test scores from a given class of analytical functions. Also, computers make it possible to quite simply implement the time-consuming, manual execution of the transition procedure to normally distributed estimates by digitizing the output test indicator. This procedure is usually simultaneously used to bring test scores to a standard form and will be discussed in detail below.

Convert test scores to standard form.

Under the standard form understand the linear transformation of the normal (or artificially normalized) test scores of the following type

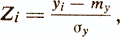
where Z i is the standard test score of the i-th subject;

yi is the normal score of the i-th subject;

tu and σ y is the arithmetic mean and the standard deviation of y.

Standard Z-scores are distributed according to the normal law with zero mean and unit variance. This is useful for benchmarking standard evaluations of various psychodiagnostic indicators. But since Z-scores can take fractional and negative values, which is inconvenient for perception, in practice weighted standard scores (Vi) are more often used.

Vi = a + bZi,

where a and b are the centering and proportionality constants, respectively. Parameter a makes sense in this case, the arithmetic mean value of the weighted standard estimate V, a b is interpreted as the standard deviation V.

In psychodiagnostics, the following centering and proportionality constants are most popular (General psychodiagnostics, 1987):

1. T-scale MacColl - a = 50, b = 10.

2. Scale IQ - a = 100, b = 15.

3. Stanine scale (integer values ​​from 1 to 9 - standard nine) - a = 5.0, b = 2.

4. The “stanov” scale (standard ten) is a = 5.5, b = 2. As mentioned earlier, computers make it quite easy to nonlinearly normalize raw test values ​​of y and move on to weighted standard estimates in any of the above scales. The procedure for such a transition is a new digitization of u and may look, for example, as follows. For any mark of the selected standard scale V , its percentile rank PR (Vk) = С is known . It is equal to the area under the theoretical normal distribution curve with the mean a and the standard deviation b calculated for V and multiplied by 100. The histogram of the empirical distribution of raw test scores is used to find the point yi, which corresponds to the same percentile rank PR (yi) = C . After this mark yi is assigned a new value Vk. This is how all values ​​of V are transferred to y.

Quantile standardization.

An example of quantile standardization is the percentile standardization, when a new value of its percentile rank PR (y) is assigned to the “raw” scale y . Quantile is a general concept, special cases of which may be, for example, except percentiles, quartiles, quintiles and deciles. Three apartment marks (Q1, Q2, Q3 ) break the empirical distribution of test scores into 4 parts (quarts) in such a way that 25% of subjects are below Q1, 50% below Q2 and 75% below Q3. Four quintels (K1, K2, Kz, K4) divide the sample in the same way into 5 parts with a step of 20% and nine deciles (D1, ..., D9) divide the sample into ten parts with a step of 10%.

The corresponding quantile number is used as the new converted test score. The quantile scale differs in that its construction is in no way connected with the type of distribution of primary test scores, which may be normal or have any other form. The only condition for its construction is the possibility of ranking the subjects by the value of y. Quantile ranks have a rectangular distribution, that is, each interval of the quantile scale contains the same proportion of the examined persons / B. V. Kulagin, 1984 /. Standardizing test scores by translating them into a quantile scale erases the differences in the features of the distribution of psychodiagnostic indicators, since it reduces any distribution to a rectangular one. Therefore, from the standpoint of the theory of measurements, quantile scales refer to scales of order: they provide information on which of the subjects tested property is more pronounced, but they do not allow us to say anything about how much or how many times stronger.

The constructed diagnostic model can be considered a psychodiagnostic test only after passing comprehensive tests for the assessment of psychometric properties. The main psychometric properties of psychodiagnostic methods, except for standardization, are reliability and validity / Anastasi A., 1982; Gaida, V.K. et al., 1982; Gilbukh Yu. 3., 1982; 1986; Kulagin B.V., 1984; General Psychodiagnostics, 1987; Burlachuk LF, et al., 1989 /.

The reliability of the test is a characteristic of the technique, reflecting the accuracy of psychodiagnostic measurements, as well as the stability of the test results to the action of extraneous random factors / Burlachuk LF et al., 1989 /.

The result of psychological research is usually influenced by a large number of unrecorded factors (for example, emotional state and fatigue, if they are not included in the range of studied characteristics, light, temperature and other features of the room in which testing is carried out, the level of motivation of the subjects, etc.). Therefore, any empirically obtained estimate for the test yi is represented as the sum of the true estimate of y ¥ and the measurement error ε: yi = y ¥ + e. In order to analyze the reliability, the concept of “parallel tests” is introduced, which are tests that measure this property equally by means of the same actions and operations / Kulagin B. V., 1984 /. This concept is generalized, since parallel tests can be both parallel forms and repeated examinations of subjects with the same method. If one assumes that the properties measured by individuals change little over time, and the errors are completely random and non-systematic, then parallel tests give results with the same mean values, standard deviations, intercorrelations and correlations with other variables.

The reliability coefficient Ryy is defined as the correlation of parallel tests, which, in turn, is equal to

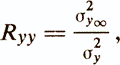
where σ2u ¥   Is the variance of the true estimate, and σ2у is the variance of the empirical estimate.

The correlation of parallel tests with any other variable z is determined by the ratio

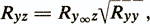
where is Ry ¥ z   - correlation of true estimates of i> y ¥ with variable z. This formula shows that the correlation of the test with any external variable is limited by the reliability coefficient. For example, if the correlation of the true estimate of y ¥ with the variable z ( Ry ¥ z ) is 1.0, and the reliability coefficient (Ryy) is 0.70, then the empirical correlation (Ryz) will be 0.84.

The reliability coefficient is related to the standard measurement error (σε is the standard deviation of measurement errors ε)

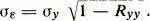
It follows that with an increase in the reliability coefficient Ryy , the error σε decreases.

Correlation of empirical and true Ryy ¥ estimates   called the reliability index and is determined by the ratio

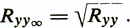
There are three main approaches to assessing the reliability of tests, which differ in factors taken as measurement errors.

Test retest reliability. The reliability coefficient (Ryy) is measured by re-examining the same subjects over a certain time period and is equal to the correlation coefficient of the results of the two tests. Measurement errors in this case are due to differences in the condition of the subjects, organization and conditions of repeated examinations, memorization of answers, the acquisition of skills to work with the test, etc. Test-retest reliability is also called reliability - sustainability.

Reliability of parallel test forms . The reliability coefficient is equal to the correlation of parallel test forms. Measurement errors in this case, in addition to the above factors, are associated with differences in the nature of the actions and operations inherent in parallel forms of the test. The high value of the correlation coefficient, in addition to the high reliability of the results of the compared tests, indicates the equivalence of the content of these tests. Therefore, the reliability coefficient for parallel forms of the test is another name - equivalent reliability.

Reliability as homogeneity of tests. In this case, reliability is estimated by calculating the intercorrelations of parts or elements of the method, considered as separate parallel tests. This approach is valid for the evaluation of tests, the construction of which used a diagnostic model based on the criteria of autoinformativeness of the system of initial features (based on the principle of internal consistency of test tasks). The most common procedure splitting the test into two parts: one includes, for example, the results of even tasks, and the other odd. To determine the reliability of the whole test, the Spearman-Brown formula is used:

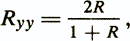
where R is the correlation between the dough halves.

Taking into account the fact that a test built on the principle of internal consistency of tasks can be split into parts in different ways, the Cronbach coefficient is often used in psychometrics to assess reliability

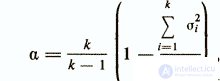
where a is the designation of the Cronbach coefficient;
k is the number of test tasks;
σ2 i is the variance of the i-ro test item;
σ2у —dispersion of the whole test.

If the answers to each item of the test are dichotomous variables, then the Cüder-Richardson formula, similar to the Kronbach coefficient, is used.

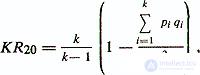
where KR20 is the traditional designation of this safety factor;
pi is the share of the 1st answer to the i-th question;
qi = (1 - pi) - the proportion of the second answer to the i-question.

Other safety factors for homogeneous tests are known. Most of the criteria underlying these coefficients are based on the fact that the matrix of the intercorrelation of tasks of a reliable test has a rank close to one. For example, the coefficient applied is called theta reliability of the test / General Psychodiagnostics, 1987 /:

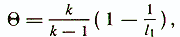
where k is the number of test items.

l1 is the largest eigenvalue corresponding to the 1st main component of the test point intercorrelation matrix.

The above formulas can be used only when each subject is working with all the elements of the test. This applies to techniques that do not have time limits. Regardless of the fulfillment of this condition, the reliability of individual psychodiagnostic test items is often assessed.

The reliability of individual test items. Retest reliability of the test as a whole depends on the stability of the answers of the subjects to individual test items. To test this robustness, a correlation is calculated between the answers of the subjects to the item being checked and the answers during repeated testing. For dichotomous items, the coefficient φ is usually used and the point is considered not sufficiently stable if φ <0.5.

Also, the so-called discriminativeness of test assignments is often checked / Burlachuk LF et al., 1989 /, which refers to the ability of individual items to differentiate the subjects with respect to the “maximum” or “minimum” test result as a whole. The procedure of checking the reliability of items is aimed at improving the internal consistency of the test and corresponds to the previously described method of contrasting groups. As a measure of the reliability point can be used the coefficient φ . In addition, the point-based bisterial correlation coefficient r rv, which in this case is called the discrimination coefficient (index), is often used.

In contrast to reliability, validity is a measure of the conformity of test evaluations to the ideas about the nature of properties or their role in a particular activity / Kulagin B.V., 1984 /. There are three main types of validity - content, empirical (criterial) and construct (conceptual).

Content validity characterizes the degree of representativeness of the content of the test tasks of the measured area of ​​mental properties / Burlachuk LF et al., 1989 /. Traditionally, this characteristic has the greatest value for tests that investigate activities that are close to or coincide with real (most often academic or professional). Since this activity often consists of heterogeneous factors (manifestations of personality abilities, a complex of necessary knowledge and skills, specific abilities), the selection of tasks covering the main aspects of the phenomenon under study is one of the most important tasks of forming an adequate model of the activity being tested. The validity of the content is laid in the test already in the selection of tasks for the future methodology. This question is discussed above when it came to the formation of the initial set of diagnostic features. The conclusion about the substantive validity, as a rule, is made by experts, who make a judgment about the extent to which this test covers the declared properties and phenomena.

Content validity must be distinguished from obvious, facial, external validity, which is such from the point of view of the subject. Obvious validity means the impression about the subject of measurement, which is formed in the subjects when they get acquainted with the instruction and test material. It also plays a significant role in testing, since it primarily determines the attitude of the subjects to the examination. Therefore, the obvious validity is sometimes called trust validity. In some cases, the content and external validity coincide, in others - obvious validity is used to mask the true objectives of the study.

Empirical validity - a set of characteristics of the validity of the test, obtained using comparative statistical analysis. The indicator of empirical validity is expressed by a quantitative measure of the statistical relationship between the test results and the external criteria for evaluating the diagnosed property. As such criteria, expert assessments, experimental and “life” criteria, which have already been considered before, can be used. Empirical validity is most often expressed by the correlation coefficient of test results y with the criterion index z. It is known that the correlation of two variables depends on their reliability:

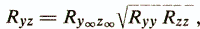
where Ry ¥ z ¥ is the correlation between the true values ​​of the test and the criterion; Ryy - test reliability; Rzz - criterion reliability. This formula shows that the maximum possible validity is limited by the reliability values ​​of the test and the external criterion.

Empirical validity may be represented by other indicators. For example, if the external criterion is characterized by a dichotomous variable, the percentage of persons whose assessments are in the overlap of the distribution of indicators by test in dichotomous groups can act as an indicator of empirical validity / Dunnette MD, 1966 /. Also a common way of presenting a statistical connection of test results is a tabular form in which the intervals of test scores are compared with the probabilities of the subjects belonging to different diagnostic classes.

When evaluating the empirical validity of tests, it is necessary to establish it in at least 2 groups, since the correlation between the test and the criterion may be due to factors specific to the sample and not have a common meaning / B. Kulagin, 1984 /. It is especially important that the validity of the test is determined on a sample of subjects, different from the one with which the selection of tasks was carried out / Anastasi A., 1982 /. To fulfill this condition, it is possible, for example, to split the available experimental material in half. At the same time, it is preferable to conduct several studies with subsequent analysis and synthesis of the data obtained.

Constructive validity is the validity of the test in relation to a psychological concept - a scientific concept (or their totality) about a measured mental property (state). It expresses the degree of validity of the individual differences found by the test from the standpoint of modern theoretical knowledge. A common method of determining the constructive validity of a test is its correlation with known methods, reflecting other constructs, presumably both related and independent of this one. An attempt is made to a priori predict the presence or absence of a connection between them. Tests that are supposedly highly correlated with a validating test are called converging, and non-correlating tests are discriminant. Conceptual validity can be considered satisfactory if the correlation coefficients of a validated test with a group of converging tests are statistically significantly higher than the coefficients of correlation with a group of discriminant tests. Confirmation of a set of expected relationships constitutes an important range of constructive validity and is also called “presumptive validity” in foreign literature.

In conclusion, the chapters will present in a compressed form all the stages of constructing a psychodiagnostic test and briefly describe the main operations at these stages. Modern methodology of psychological testing considers the most optimal rational-empirical strategy for solving this problem / General psychodiagnostics, 1987 /.

1) Formation of the initial version of the psychodiagnostic test.

- Theoretical analysis of the diagnosed construct, the development of the theoretical concept of the tested property. Identification (using literature) of a system of interrelated diagnostic constructs, within which a new diagnostic construct is characterized by certain structural and functional connections and relationships. Prediction of the results of correlation experiments to verify constructive validity.

- Isolation of the constituent parts of a theoretical construct, the formation of a system of "empirical indicators" (system of initial features) - operationally unambiguous indicators that fix the manifestation of the construct in various behavioral situations. Designing test items.

In case of borrowing of separate parts of a new test, well-known psychodiagnostic methods are used to select such methods (as a rule, multidimensional tests), some of which are theoretically capable of reflecting the required diagnostic property.

- Formulation of a relevant external criterion that will be used to verify the empirical validity of the test and can also be used in empirical-statistical data analysis to determine the parameters of the diagnostic model.

2 ) Conducting experimental surveys and determining the parameters of diagnostic models.

- Planning and conducting a survey of the original version of the psychodiagnostic test of a specially selected sample of subjects for whom the values ​​of the criterion indicator are known (or will be known), as well as the results of related tests. If necessary, additional tests are carried out on these subjects in order to ensure further verification of the constructive validity of the new test (expert assessments in this case are considered as one of the parallel procedures for obtaining criteria or psychological information).

Currently, there is no unequivocal answer to the question about the size of the sample being surveyed. At least, such a response cannot be given a priori until an exploratory statistical analysis is carried out and the type of distributions of the variables studied are established. The study of a large number of real-world problems of multidimensional data analysis shows that the bulk of the experimental data tables used contained from 30 to 200 objects and the median of the empirical distribution of the sample size was 100 / V. V. Aleksandrov and others, 1990 /. Depending on the sample size, different statistical criteria are used. The problem of small sampling in the construction of linear decision rules is considered, for example, in / Raudis S. et al., 1975 /.

- Determination of the parameters of diagnostic models (selection of informative test items, finding weighting factors) is performed using the methods of multivariate statistical analysis described in this chapter. These methods are fully implemented in almost all known software packages for statistical data processing such as STATGRAPHICS, SPSS, BMDP, which operate on personal computers. However, as noted above, the specificity of psychological measurements (high dimensionality, nominal and qualitative character of the initial features) leaves its mark on the use of these methods in psychodiagnostics. Often it is impractical, and even impossible to use the classic version of a method. Often, it makes sense for a researcher to limit himself to simplified models of these methods and to focus on their implementation in the form of feature selection and the most approximate assessment of weights for test items that are included in the rule for calculating the resulting psychodiagnostic indicator.

3) Analysis of the distribution of test points, the construction of test standards and verification of their representativeness.

Table. Methods for determining the parameters of diagnostic models

Open the table »» »

When building test norms, the psychologist must perform the following actions / General Psychodiagnostics, 1987 /.

- Form a sample of standardization (random or stratified by any parameter) from the population on which the test is supposed to be applied. Conduct a test on every test subject in a short time (to eliminate the irrelevant variation caused by external events that occurred during the survey).

- To group the "raw" points based on the selected quantization interval.

- Build the distribution of frequencies of test points (for given intervals) in the form of a table and in the form of the corresponding graphs of the histogram and cumulates.

- To calculate the average and standard deviations, as well as asymmetry and kurtosis. Test hypotheses about the significance of asymmetry and kurtosis. Compare test results with visual analysis of distribution curves.

- Check the normality of the distribution of frequencies of test points using, for example, the Kolmogorov criterion or using other more powerful criteria.

- If the hypothesis of normal distribution is rejected, perform a percentile normalization with translation to the selected standard scale. Check the stability of the distribution by splitting the sample into two random halves. If the normalized scores match for half and for the whole sample, consider the normalized scale to be stable.

- Check the uniformity of distribution with respect to the variation of a given population trait (gender, profession, etc.) using the Kolmogorov criterion. Construct in combined coordinates histogram graphs and cumulates for complete and private samples. With significant differences in these graphs, split the sample into heterogeneous samples.

- Build tables of percentile and normalized test norms (for each interval of "raw" points). If there are heterogeneous samples, each of them has its own table.

- Determine the critical points (upper and lower) for the confidence intervals (at the level of -P

- Discuss the configuration of the obtained distributions taking into account the proposed mechanism for solving one or another test.

- In case of negative results - lack of stability of norms for a scale with a given number of gradations (with a given accuracy) - carry out a survey of a wider sample or abandon the plan for using this test.

4) Reliability analysis.

- For tests built on the principle of internal consistency (without using external criteria), the reliability coefficients are calculated using the formulas 2.69-72.

- If there are results of the standardization sample survey with parallel test forms, then the correlation coefficients of these results with the points obtained using the new test are calculated.

- Testing reliability as resistance to retesting is absolutely necessary in the diagnosis of properties, in relation to which, invariance in time is theoretically expected. The analysis of retest reliability can be (as well as the analysis of reliability - consistency) combined with the study of the informativeness of individual items.

5) Analysis of validity.

The correlation coefficients of the constructed test with the relevant external criterion are calculated, as well as with the results of additional tests for the evaluation of construct validity.

The requirements for a psychometrist who develops a psychodiagnostic test are set forth in / Burlachuk LF et al., 1989 /. It also sets out the requirements for the use of computers in psychodiagnostics.

LITERATURE

1. Avanesov V.S. Tests in a sociological study. - M., 1982. —199 p.
2. Automation of methods of psychological research: principles and recommendations. - Eagle: Institute of Labor Protection. —1989. —326 s.
3. Ayvazyan S. A., Bezhaeva 3. I., Staroverov O. V. Classification of multidimensional (observations. - M .: Statistics, 1974. —240 p.
4. Ayvazyan S. A., Enyukov I. S., Meshalkin L. D. Applied statistics. Basics of modeling and primary data processing. - M .: Finance and Statistics, 1983. —471 p.
5. Ayvazyan S. A., Enyukov I. S., Meshalkin L. D. Applied statistics. Statistical estimation of dependencies. - M .: Finance and Statistics, 1985. - 484 p.
6. Ayvazyan S. A., Buchstaber V. M., Enyukov I. S., Meshalkin L. D. Applied statistics. Classification and reduction of dimension. - M .: Finance and Statistics, 1989. —607 p.
7. Aleksandrov V.V., Alekseev A.I., Gorsky N.D. Analysis of computer data (using the SITO system as an example). - M .: Finance and Statistics, 1990. —192 p.
8. V. Aleksandrov, V. I. Lachinov, A. A. Polyakov. Recursive algorithmization of a curve that fills a multidimensional interval, Izv. USSR Academy of Sciences: Tech. Cybernetics, 1978, № 1. - p. 192-197.
9. Aleksandrov V.V., Schneider V.S. Processing of biomedical data on a computer. - M .: Medicine, 1984. —157 p.
10. Anastasi A. Psychological Testing: Book 2. Trans. from English / Ed. Gurevich K. M., Lubovsky V. I. - Moscow: Pedagogy, 1982.
11. Anderson T. Introduction to multivariate statistical analysis. - M .: Fiz-Matgiz, 1963. —500 p.
12. Antsyferova L.I. System Approach in Personality Psychology // Collection: The Principle of Systematization in Psychological Research. - M .: Science, 1990. - p. 61-77.
13. Arkad'ev, AG, Braverman, E.M. Training of object classification machines. - M .: Science, 1971. —172 p.
14. Aho A., Hopkroft J., Ulman J. Construction and analysis of computational algorithms. - M .: Mir. —329 s.
15. Barabash B. A. Minimization of description in the tasks of automatic pattern recognition // Tehn. Cybernetics, 1964, № 3. - p. 32-44.
16. Belyuk L.V. Complex system implementation of the tasks of vocational guidance with the use of computers. - M., 1988. —88 p.
17. Berezin F. B., Miroshnikov M. P., Rozanets R. V. Methods of multilateral personality research. - M .: Medicine, 1976.
18. Bespalko IG, Gilyasheva I.N. Projective methods // Methods of psychological diagnosis and correction in the clinic. - L .: Medicine. - with. 116-144.
19. Bobrov A.Ye., Shurygin A.I. Alcohol screening test: its validity and structure // Psychological diagnostics in neuropsychiatric and psychosomatic diseases. - L .: Institute of Psychoneurology. V.M. Bekhtereva, 1985. - p. 33-36.
20. Bonner R.E. Some classification methods // Automatic Image Analysis. —M .: Mir, 1969. - p. 205-234.
21. Brusentsov N. P., Galimov Yu. Yu., Maslov S. P., Ramil A. Kh. Automated learning system “Mentor”. - M., 1975.
22. The future of artificial intelligence / Ed. K. E. Levitin and D. A. Pospelov - Moscow: Nauka, 1991. —302 p.
23. Bukatova I. L. Evolutionary modeling and its applications. - M .: Science, 1979. —231 p.
24. Burlachuk LF, Morozov S.M. Dictionary-reference book on psychological diagnostics. - Kiev: Naukova Dumka. —1989. —200 sec.
25. Bushurova V. G. Diss. on the competition uch. Art. Cand. psychol. sciences. - LSU, -1988.
26. Weinzweig M.N. Algorithm for Learning Pattern Recognition “Bark” // Algorithms for Learning Pattern Recognition. - M .: Owls. radio, / 973. - with. 8-12.
27. Vapnik V.N., Chervonenkis A. Ya. The Theory of Pattern Recognition / (statistical problems of learning). - M .: Science, 1974. - 415 p.
28. Vasilyev V.I. Recognition Systems. Directory. - Kiev: Naukova Dumka, 1983. - 422.
29. Veselkov, A.F., On the Principles of Creating an Automated Base for Experimental Psychological Research, Psychol. jury - V. 8, № 3. —1987. - with. 130-136.
30. Veshtorr AM, Zuev Yu. A., Krasnoproshin V.V. Two-level recognition scheme with a logical corrector // In the book: Recognition, classification, forecast. Mathematical methods and their application. - M .: Science, 1989. - Vol. 2. - s. 73-98.
31. Vorobyov V.M., Burov V.V., Dyuk V.A. Experience of medical and psychological examination of some contingents of young people // Healthcare of the RSFSR, 1984, No. 2. - p. 37.
32. Vorobiev V.M., Dyuk V.A., Iovlev B.V., Senopalnikov E.V., Chigirev V.A. Development of an automated psychodiagnostic system for mass prophylactic examination // Study of the mechanisms and effectiveness of psychotherapy in neuropsychiatric diseases . - L .: Institute of Psychoneurology. V.M. Bekhtereva, 1981.
33. Vorobyov V.M., Dyuk V.A. The use of standardized questionnaires for the rapid diagnosis of neuropsychiatric disorders // Psychological diagnosis in neuropsychiatric and psychosomatic diseases. - L .: Institute of Psychoneurology. V.M. Bekhtereva. —1985. - with. 27-28.
34. Vorobiev V.M., Dryzgo N.P., Dyuk V.A., Savvin Yu. B., Chigirev V.A. Scientific and methodological recommendations on the use of a standardized personal questionnaire for medical and psychological examination of candidates for higher educational institutions. —L.: Ministry of Defense of the USSR, 1984. —32 p.
35. Tatiana A. Gavrilova. Knowledge Representation in the AVTANTEST Expert Diagnostic System // Izv. Academy of Sciences of the USSR. Tech. Cybernetics, 1984, № 5. - p. 168-175.
36. T. A. Gavrilova, K. R. Chervinskaya, A. M. Yashin. Forming the Field of Knowledge on the Example of Psychodiagnostics. Izv. Academy of Sciences of the USSR. Tech. Cybernetics, 1988, № 5. - p. 72-85.
37. Gaida V. K., Zakharov V. P. Psychological testing. —L.: Publishing house of Leningrad State University, 1982. —101 s.
38. Ganzen V. А. System descriptions in psychology. - L .: Publishing House of Leningrad State University, 1984. —175 p.
39. Gannushkin P. B. Clinic of psychopathy, their statics, dynamics. - M .: Medicine, 1939. —309 p.
40. Gilbukh Yu. 3. The method of psychological tests: the nature and significance // Vopr. Psychology., 1986, № 2. - p. 30-42.
41. Glasse J., Stanley J. Statistical methods in pedagogy and psychology. - M .: Progress, 1976 - 495 p.
42. Govorkova, A. F., Experience in the Study of Certain Intellectual Abilities, Vopr. Psychology, 1962, No. 2. 83-91.
43. Gorelik A. L., Skripkin V. A. Recognition methods. - M .: Higher School, 1989. —232 p.
44. Gorelik A. L., Gurevich I. B., Skripkin V. A. The current state of the problem of recognition: Some aspects. - M .: Radio and communication, 1985.
45. Gorsky ND. Recursive method of displaying multidimensional space when solving problems of data storage and processing in automated
46. research systems. - Author. on the competition uch. step. Cand. tech. sciences. —L., 1981. —19 s.
47. R. Granovskaya, I. Bereznaya, I. Ya. Intuition and Artificial Intelligence .-- Leningrad: Leningrad State University, 1991. - 272 p.
48. T. A. Guberman, L. T. Yampolsky. Application of Pattern Recognition Algorithms in Psychodiagnostics. Vopr. Psychology, 1983, No. 5. - p. 118-125.
49. Gubler Ye. V. Informatics in pathology, clinical medicine and pediatrics. —L .: Medicine, 1990. —176 p.
50. Deev A.A., Lozhkin G.V., Spasennikov V.V. Automated survey procedure using a sixteen-factor personality survey // Psychol. Zh., 1984, № 6. - p. 106-111.
51. Demidenko E. 3. Linear and nonlinear regression. - M .: Finance and Statistics, 1981. —302 p.
52. Digo S. M. Database Design. - M .: Finance and Statistics, 1988.
53. Draper N., Smith G. Applied Regression Analysis. - M .: Statistics, 1973. —392 p.
54. Duda R., Hart P. Pattern Recognition and Scene Analysis. - M .: Mir, 1976. —511 p.
55. Davison M. Multidimensional Scaling: Methods for Visual Presentation of Data. - M .: Finance and Statistics, 1988.
56. Dyuk V. А. Problems of Applying Formal Meta-Forming Formation Methods for Conceptual Analysis of Knowledge // Methods and Decision Making Systems. Knowledge-based design support systems. - Riga: Riga. tech. un-t 1991. - p. 90-95.
57. Eliseeva I. I., Rukavishnikov V. O. Grouping, correlation, pattern recognition (Statistical methods of classification and measurement of communication). - M .: Statistics, 1977. —144 p.
58. Enukov I. S. Methods, algorithms, programs for multivariate statistical analysis: PPSA package. - M .: Finance and Statistics, 1986. —232 p.
59. Ermakova I. V. Automated system ALICE as an instrument of an experimental psychologist // Vopr. Psychology, 1984, № 3. - p. 141-144.
60. Ermakova I.V. Some approaches and prospects for the development of automated psychodiagnostics and forecasting abroad // Vopr. Psychology, 1986, № 4. - p. 170-175.
61. Zhambju M. Hierarchical cluster analysis and correspondences. - M .: Finance and Statistics, 1988.
62. Zhitkov G. N. Some methods of automatic classification // Structural methods of identification and automatic reading. M .: VINITI, 1970. - p. 68-85.
63. Yu. I. Zhuravlev. Non-parametric problems of pattern recognition // Cybernetics, 1976, No. 6. - p. 93-103.
64. Zhuravlev Yu. I. On the algebraic approach to solving recognition and classification problems // Problems of Cybernetics. - M .: Science, 1978, vol. 33. - p. 5-68.
65. Zhuravlev Yu. I., Gurevich I. B. Pattern Recognition and Image Analysis / Artificial Intelligence. - V. 3 kN. Prince 2. Models and methods: Handbook / ed. D. A. Pospelov. —M .: Radio and communications, 1990. —304 p.
66. Zabrodin Yu. M. The development of Soviet psychology and the tasks of psychological service // Psychol. Zh., 1984, № 6. - p. 3-20.
67. Zabrodin, Yu.M., Pokhilko, V.I., Shmelev, A.G., Statistical and Semantic Problems of Designing and Adaptation of Multifactorial Personality Test Questionnaires, Psychol. Zh., t. 8, No. 6, 1987. - p. 79-89.
68. Zagoruiko NG. Methodology for evaluating the information effectiveness of independent parameters of a speech signal // Tr. IM Sib. Dep. USSR Academy of Sciences: Computing Systems, 1964, no. 10. - s. 77-89.
69. Zagoruiko N. G. Recognition methods and their application. - M .: Owls. radio, 1972. —206 p.
70. Zagoruiko N. G., Elkina V. N., Lbov G. S. Detection Algorithms of Empirical Regularities. - Novosibirsk: Science, 1985. —110 p.
71. Zade L. The concept of a linguistic variable and its application to making approximate decisions. - M .: Mir, 1976.
72. Zaks L. Statistical Evaluation. - M .: Statistics, 1976.
73. Zelichenko A. I. Intellectual systems and psychological knowledge // In the book: Computers and cognition. - M .: Science, 1990. - p. 69-86.
74. Zelichenko A.I. Some extremal pattern recognition problems. - Diss. on the competition uch. step. Cand. Phys.-Mat. sciences. - M., 1982.
75. Iberla K. Factor analysis. - M .: Statistics, 1980. —308 p.
76. Ivakhnenko A. G. Self-learning systems of recognition and automatic control. - Kiev: Technique, 1969. —392 p.
77. Artificial Intelligence: In 3 kN. Prince 1. Communication systems and expert systems: a Handbook / ed. E. V. Popova. - M .: Radio and communication, 1990. - 464 p.
78. Artificial Intelligence: In 3 kN. Prince 2. Models and methods: Handbook / ed. D. A. Pospelov. - M .: Radio and communication, 1990. —304 p.
79. Kalnish V.V., Romanenko E.V., Samoilov V.D. System architecture and software development and automation of diagnostics of psychological and psychophysiological qualities of operational dispatch personnel. - Kiev: Inst. modeling in power engineering, 1989. —53.
80. Karvasarsky B.D. Medical psychology. - L., 1982.
81. Karvasarsky B.D. Neurosis. - M., 1980.
82. Kendall M. Methods of rank correlation. - M .: Statistics, 1974.
83. Kendall M., Stuart A. Statistical Findings and Links. - M .: Science, 1973. —900 p.
84. Classification and Cluster / ed. J. Van Raizin. - M .: Mir, 1980. - 390 p.
85. Knut D. The Art of Computer Programming. T. 1. - M .: Mir, 1977.
86. Kolesov V. V. Reflection of the Russian mentality in the word / Man in the mirror of sciences. —L .: Leningrad State University, 1991. - p. 106-124.
87. Kolmogorov A.N. Three approaches to the definition of the concept “quantity of information” // Problems of information transfer / ed. Yagloma P.S., 1965, vol. 1, no. one.
88. Konovalova NL. Psychological factors of social and labor rehabilitation of patients with chronic cerebrovascular insufficiency. - Diss. on the competition uch. Art. Cand. psychol. sciences. - Institute of Psychoneurology. V.M. Bekhtereva, 1989.
89. Kofman A. Introduction to applied combinatorics. - M .: Science, 1975. - 286 p.
90. Krylov V.Yu. Method of multidimensional geometrization of psychological data, a systematic approach in mathematical psychology // Principle of systematicity in psychological research. - M .: Science, 1990. - p. 33-48.
91. Kuznetsov A.S. Methods for searching for optimal groups of features in statistical pattern recognition. - L .: VIKI them. A.F. Mozhaisky, 1982. - p. 14-23.
92. Cook N. M., MacDonald J. Formal Methodology of Acquisition and Representation of Expert Knowledge // TIIER, 1986, vol. 74, No. 10. - p. 145-155.
93. Kulagin B.V. Fundamentals of professional psychodiagnostics. - L .: Medicine, 1984. —216 p.
94. Kulagin B.V., Sergeev S.T. Typological approach to the study of the problem of professional selection // Psychol. Zh., 1989, t. 10, № 1.
95. Lbov G.S. Choice of an effective system of dependent features / Works Sib. Dep. USSR Academy of Sciences: Computing Systems. - Novosibirsk, 1965, no. 19. - p. 87-101.
96. G. Lbov. Logic Functions in Empirical Prediction Problems // Empirical Prediction and Pattern Recognition: Computational Systems. - Novosibirsk, 1978, vol. 76. - p. 34-64.
97. Lbov G.S. Methods for processing different types of experimental data. - Novosibirsk: Science, 1981. —157 p.
98. Lichko A.E., Ivanov N.Ya. Pathocharacterological diagnostic questionnaire for adolescents and the experience of its practical use. - L .: Medicine, 1976.
99. Lichko A.E. Psychopathy and character accentuation in adolescents. - L .: Medicine, 1983. —225 p.
100. Lomov BF On the system approach in psychology // Vopr. Psychology., 1975, № 2. - p. 31-45.
101. Lomov BF On the systemic determination of mental phenomena and behavior / / Coll .: The principle of consistency in psychological research. - M .: Science, 1990. - p. 10-17.
102. Lawley D., Maxwell A. Factor analysis as a statistical method. - M .: Mir, 1967. —144 p.
103. Moller F., Kapekki V. The role of entropy in the nominal classification // Mathematics and sociology. - M., 1977. - p. 301 -338.
104. Melnikov A.V. On the use of personal computers in psychology // Psychol. Zh., t. 10, No. 1, 1989. - p. 56-61.
105. Melnikov V. M., Yampolsky L. T. Introduction to experimental psychology of personality. - M .: Enlightenment, 1985. —319 p.
106. Method of determining the level of neuroticism and psychopathization. - L .: Institute of Psychoneurology. V.M. Bekhtereva, 1980. - 45 p.
107. Methodological manual on the organization and conduct of a psychiatric examination of candidates for higher educational institutions / ed. Spivak L.I. - Ministry of Defense of the USSR, 1980. - 46 p.
108. Methods and technical means of psychological diagnosis: mes. scientific message All-Union. conf. / resp. ed. Zabrodin, Yu. M., Plotnikov, V. V. - Oryol: All-Russian Scientific and Research Institute of Labor Protection, 1988. –175 p.
109. Meshalkin L. D. Local classification methods // Statistical methods of classification. - M .: MSU, 1969, vol. 1. - p. 58-78.
110. Minsky M., Papert S. Perceptrons. - M .: Mir, 1971. - 261 p.
111. Mirkin B. G. Analysis of qualitative features and structures. - M .: Statistics, 1980. - 319 p.
112. Mosteller F., Tukey J. Data Analysis and Regression. - M .: Finance and Statistics, 1982. —239 p.
113. Myasishchev V.N. Personality and Neurosis. —L .: Leningrad State University, I960. —224 sec.
114. Nazaretov V.M., Kim D.P. Technical Imitation of Intellect. Prince 6. Robotics and flexible automated production. In 9 books. / Ed. I.M. Makarova. - M .: Higher School, 1986.
115. V. Nalimov. Experiment theory. - M .: Science, 1971. —208 p.
116. Nikiforov AM, Fazylov Sh. X. Methods and algorithms for the conversion of attribute types in data analysis tasks. - Tashkent: Fan, 1988. —132 p.
117. Nilson N. Principles of Artificial Intelligence. - M .: Radio and communication, 1985.
118. Norakidze V. G. Methods of personality research. Tbilisi: Metsniereba, 1975. —243 p.
119. Standard prescriptions for developers and users of psychodiagnostic methods // Vopr. Psychology., 1987, No. 5. - p. 176-181.
120. Oganezov A.S., Sumenko O.V. Automation of personality research using the psychological method MMPI with the synthesis of verbal diagnosis // Vopr. psychol., 1990, № 1. - p. 154-157.
121. S. Papovyan. Experiment in Applied Social Psychology: Actual Problems of Statistical Data Analysis // Psychol. Journal, Vol. 6, No. 6, 1985. - p. 90-100.
122. Patrick E. Fundamentals of the theory of pattern recognition. - M .: Owls. Radio, 1970. —408 p.
123. Petrenko V.F. Introduction to Experimental Psychosemantics: A Study of the Form of Representation in the Common Consciousness. - M .; 1983. —127 sec.
124. Petrenko V.F., Pronina E.E. The Man on the TV Screen: The Experience of Psychological Research // Psychol. Zh., 1986, t. 7, № 3. - p. 62-70.
125. Pirov GD Classification of methods in psychology. - Bratislava: Psychodiagnostics in the socialist countries, 1985. - p. 19-25.
126. Popechitelev E. P., Romanov S. V. Analysis of numerical tables in biotechnical systems for processing experimental data. - L .: Science, 1985. - 148 p.
127. Popov E.V. Expert systems. Solving non-formalized tasks in a dialogue with a computer. - M .: Science, 1987. —288 p.
128. Popov E. V. Features of the development and use of expert systems // Artificial Intelligence. Prince 1: communication systems and expert systems. - M .: Radio p communication, 1990.
129. Pospelov D. A. Situational management. - M .: Science, 1986. —288 p.
130. Pospelov D. A. Data and knowledge. Knowledge representation // Artificial Intelligence. Prince 2: Models and methods: Reference / ed. D. A. Pospelov. - M .: Radio and communication, 1990. - p. 7-13.
131. Pohilko, V.I., Fedotova, E.O., Technique of repertory grids in experimental psychology of personality, Vopr. Psychology., № 3, 1984. - p. 151-157.
132. Workshop on General and Experimental Psychology / ed. A. Krylova - L .: LSU, 1987. —255 p.
133. Workshop on psychodiagnostics. Differential psychometric / ed. V. V. Stolin, A. G. Shmelev - Moscow: Moscow State University, 1984. —151 p.
134. Representation of knowledge in man-machine and robotic systems. Applied man-machine systems, knowledge-oriented / ed. Pospelova G. S. - Moscow: The Computing Center of the USSR Academy of Sciences, VINITI of the USSR Academy of Sciences, 1980.
135. Representation and use of knowledge / ed. Ueno K., Ishizuka M. - M .: Mir, 1989.
136. Psychological diagnosis: Problems and research / ed. Gu-REVICH K. M. - M .: Pedagogy, 1981. —231 p.
137. Psychological centers of the USSR: a Handbook. - M., 1989.
138. Pfantsagl I. Measurement Theory. - M .: Mir, 1976. —248 p.
139. Pattern Recognition and Medical Diagnostics. Ed. Yu.M. Neymark - Moscow: Nauka, 1972. —328 p.
140. Pattern Recognition Using Digital Computers / Ed. Harmona L. - M .: Mir, 1974. —234 p.
141. Rastrigin L. А., Erenstein R. X. The method of collective recognition. - M .: Energoizdat, 1981. - p. 1-78.
142. Raudis S., Pikelis V., “Tabulation of the Expected Error of Classification of a Linear Discriminant Function on the Volume of a Training Sample,” Statistical Problems of Control. - Vilnius, 1975, No. 11. - p. 81-119.
143. Reshetnikov MM. Professional selection in the education system, industry and the US army // Psychol. Zh., t. 8, No. 3, 1987. - p. 145-153.
144. Rumyantsev GG. The experience of applying the method of unfinished sentences in psychiatric practice // Study of the personality in the clinic and in extreme conditions. - L .: Institute of Psychoneurology. V.M. Bekhtereva, 1969. - p. 266-275.
145. Ryabov V. B. Subbotin Yu. A. Organization of mathematical software for a complex experiment based on a display system // Methods and means of automation of psychological research. - M .: Science, 1982. - p. BUT
146. Sobchik L.N. Manual on the use of MMPI. —M .: MZ RSFSR, 1971.
147. Sokolov E. N., Izmailov I. A., Shmelev A. G., Livshits G. Ya., Tretyakov N. N. A computerized system for conducting scientific research, psychodiagnostics and training // Psychol. Journal, Vol. 6, No. 6, 1985. - p. 142-147.
148. Соловьев В. С. Сочинения. В 2-х т. — М., 1988, т. 2 — с. 174.
149. Справочник по прикладной статистике. В 2-х т. Т. 2/под ред. Ллойда Э., Ледермана У., Айвазяна С. А., Тюрина Ю. Н. — М.: Финансы и статистика, 1990. —526 с.
150. Стандартизированный клинический личностный вопросник (адаптированный И. Н. Гильяшевой, Л. Н. Собчик, Т. Л. Федоровой. Полный вариант MMPI. Мужской вариант). — Л.: НИИ психоневрологии им. В. М. Бехтерева, 1984. — 45 с.
151. Статистические методы анализа информации в социологических исследованиях/под ред. Осипова Г. В. — М.: Наука, 1979. —319 с.
152. Суппес П., Зинес Дж. Основы теории измерений // Психологические измерения. —М.: Мир, 1976. — с. 9-119.
153. Тарасов К. Е., Беликов В. К., Фролова А. И. Логика и семиотика диагноза (методологические проблемы). — М.: Медицина, 1989. —272 с.
154. Таунсенд К., Фохт Д. Проектирование и программная реализация экспертных систем на персональных ЭВМ. — М.: Финансы и статистика, 1990. — 320 с.
155. Teilhard de Chardin P. The Phenomenon of Man. — М.: Наука, 1987. —240 с.
156. Теплов Б. М., Проблема индивидуальных различий. — АПН РСФСР, 1961. —536 с.
157. Терехина А. Ю. Анализ данных методами многомерного шкалирования. —М.: Наука, 1986. —168 с.
158. Тихомиров О. К., Гурьева Л. П. Опыт анализа психологических последствий компьютеризации психодиагностической деятельности // Психол. журн., т. 10, № 2, 1989. — с. 33-45.
159. Тихомиров О. К., Собчик Л. Н., Гурьева Л. П., Гарбер И. Е., Тарновская Н. В., Ремизова А. Л. Анализ этапов компьютеризированной психодиагностики (на примере ММР1) // Вопросы психол., № 2, 1990. — с. 136-142.
160. Tu J., Gonzalez R. Principles of pattern recognition. - M .: Mir, 1978. - 412 p.
161. Tukey J. Analysis of the results of observations. Exploratory analysis. - M .: Mir, 1981. - 693 p.
162. Winston P. Artificial Intelligence. - M .: Mir, 1980.
163. Ushakova T. N. The principle of integrity in the study of psychological objects (on the material of the psychology of speech) // The principle of consistency in psychological research. - M .: Science, 1990. - p. 49-60.
164. Filmer P., Phillipson M. New directions in sociological theory. - M .: Progress, 1978. —329 p.
165. Finn. V. K. On machine-oriented formalization of plausible reasoning in the style of F. Bacon - D. S. Mill // Semiotics and Computer Science. Issue 20, 1983. - p. 35-101.
166. Fogel L., Owen A., Walsh M. Artificial Intelligence and Evolutionary Modeling. - M .: Mir, 1969. —230 p.
167. Fransella F., Bannister D. A new method of personality research. - M .: Progress, 1987. —236 p.
168. Fu K., Sequential methods in pattern recognition and machine learning. —M .: Science, 1971. - 255 p.
169. Fu K. Structural methods in pattern recognition. - M .: Mir, 1977. —320 p.
170. Fukunaga K.