Lecture
Это продолжение увлекательной статьи про конструирование психодиагностических тестов.
...
methods are implemented in the same data analysis software package, and researchers have a legitimate question about which one is better. In this matter, our opinion coincides with / Aleksandrov V.V., et al., 1990 /, where it is stated that practically all methods give very close results. The words of one of the founders of modern factor analysis G. Harman are also given there: “None of the works showed that any one method approaches the“ true ”values of communities better than other methods ... Choice among a group of methods" best "is produced mainly from the point of view of computational convenience, as well as the aptitudes and affections of the researcher, to whom this or that method seemed more adequate to his ideas of generality" / Harman G., 1972, p. 97 /.
The factor analysis has many supporters and many opponents. But, as V. V. Nalimov rightly noted: “... There were no other ways for psychologists and sociologists, and they studied these two techniques (factor analysis and the main component method, VD) with all the details” / Nalimov V.V., 1971, p. 100/. For a more detailed acquaintance with the factor analysis and its methods, literature can be recommended / Lowley, D., et al., 1967; Harman G., 1972; Ayvazyan S. A. et al., 1974; Iberla K., 1980 /.
The initial information when using the method of contrast groups, in addition to the table of experimental data with the results of examining the subjects with a “rough” version of the psychodiagnostic test, is also a “rough” version of the linear rule for calculating the tested indicator. This "draft" version can be compiled by the experimenter, based on his theoretical ideas about what signs and with what weights should be included in a linear diagnostic model. In addition, the “draft” version can be drawn from the literature when the experimenter has the need to adapt the published psychodiagnostic test to new conditions. The method of contrasting groups is also used as part of a procedure for improving the internal consistency of tasks from a previously tested test.
The method of contrasting groups is based on the hypothesis that a significant part of the “draft” version of the diagnostic model is chosen or guessed correctly. That is, in the right side of the equation uch = uch (x) there are quite a few signs consistently reflecting the property being tested. At the same time, in the “draft” version of uch (x), a certain proportion of features fall on unnecessary or even harmful ballast, which must be eliminated. As in all other methods based on the category of internal consistency, this means that in the space of features included in the original diagnostic model, the distribution of objects fits into the dispersion ellipsoid, elongated along the direction of the trend being diagnosed. In turn, the influence of the information ballast is expressed in the reduction of such an elongation of the dispersion ellipsoid, since “noisy” signs increase the scatter of the objects under study in all other directions. At the same time, the “noisiness” of the main trend will be the stronger, the closer to the distribution center the diagnosed objects are located, and the weaker the closer to the poles of the main axis of the ellipsoid of dispersion are the considered objects. This is due to the fact that the hit of objects in the extreme areas is mainly due to the cumulative effect of the coordinated interaction of informative features. Described ideas about the structure of experimental data underlie the following procedure, which will be considered on the example of the analysis of items when constructing test questionnaires / Shmelev, A. G., Pokhilko, V. I., 1985 /.
First, initial scale keys (weights) w˚j are assigned for test items (dichotomous features) xj. For each i-th test subject, the total test score is calculated
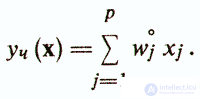
Usually, the absolute values of the weights wj are determined approximately and often taken to be equal to one. Therefore the direction
will differ somewhat from the direction of the main diagonal of the ellipsoid scattering y (x) (Fig. 3).
Fig. 3. Illustration of the contrast group method
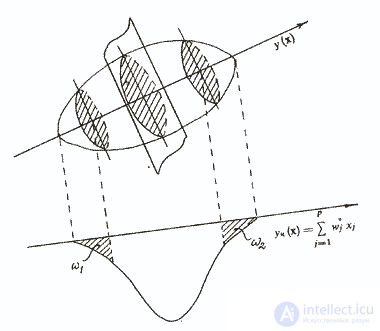
But if roughly uch (x) correctly reflects the property being diagnosed, then at the edges of the distribution of the total score constructed over all objects of the sample, we can distinguish contrasting groups ω1 and ω2, which will include objects with minimal errors introduced by "noisy" signs. These groups should not be too small. For a normal distribution, as a rule, contrast groups of 27% of the total sample size are taken, for a flatter group - 33%. In principle, any figure from 25 to 33% is considered acceptable / Anastasi A., 1982 /. The next step is to determine the degree of connection of each item with the dichotomous variable - the number of the contrast group. The measure of this connection may be the so-called coefficient of discrimination, which is the difference in percent of a response to the item being analyzed in the polar groups of subjects. The most commonly used Pearson coupling coefficient is φ, which is then compared with the boundary value
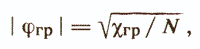
where χ2гр is the standard quantile of the distribution of χ2 with one degree of freedom. Usually they are oriented at 5% and 1% levels / significance, for which the value of χ2 is 3.84 and 6.63, respectively. If for the i-go item | φі | <| φgr |, then the weight coefficient wi is assigned the value zero, that is, the sign xi is excluded from the linear diagnostic model uch (x). Thus, all items of the “draft” version of the test are checked. Then for the remaining points the whole procedure is repeated again completely, and so on.
In practice, there is no case when the informative features finally selected by the above procedure would absolutely coincide with those originally given. The convergence of this procedure depends on the initial ratio of "good" and "bad" test tasks. Apparently, for diagnostic models based on the principle of internal consistency of the used signs, there is a certain threshold for the ratio of informative and “noisy” signs for each specific task, starting with which the self-organization effect or self-improvement of the diagnostic model can occur through the algorithm described above.
There are three main groups of external criteria: expert, experimental and "life".
Among the expert criteria are assessments, judgments, conclusions about the subjects, made by an expert or a group of experts, which are specialists, teachers, managers, psychologists, doctors, etc. Objectivization of external criteria is achieved by increasing the number of experts. In this case, four possible methods are used to determine the expert criterion: collective assessment, weighted average rating, ranking, pairwise comparison.
In a collective assessment, the experts jointly evaluate the subject by the diagnosed quality with the help of the scale scale proposed by the test developer. The condition for collective assessment is to develop a common compromise opinion. Achieving consensus in collective assessment depends on the personal characteristics and the nature of the group interaction of experts. Also an important factor is the resolution of a given rating scale. The lower the scores on this scale, the easier it is to reach agreement between the experts, but the rougher they are. At the same time, excessive specification of the scale not only does not lead to an increase in the accuracy of the assessment, but often causes unnecessary and lengthy disagreements among experts. Therefore, an estimated scale of up to 10 points is usually used.
With a weighted average of assessments, experts independently determine the values of the criterion indicator, which are then averaged. Here it is necessary to pay attention to the fact that, before averaging the estimates, the clearly deviating, anomalous estimates should be excluded from them. The ranking method, in contrast to the weighted average rating, is not associated with projecting one or another quality of the subject on a numerical rating scale, but with determining the ranks of the severity of the test quality in the group of subjects. The obtained ranking places for independent evaluation can also be averaged, but it is more correct in this case to use median estimates: each subject is assigned a rank equal to the median of a number of ranks assigned to him by all experts.
When using poorly differentiated assessment indicators or with low qualification of experts, the method of pairwise comparison is used. The task of the experts is to pair-up the placement of the subjects in terms of alternative signs (“outgoing-closed”, “envious-disinterested”, etc.). The total number of preferences of a given subject most often serves as an indicator of the place occupied by others. This indicator is usually normalized in relation to the number of experts and the total number of compared subjects and is expressed as a percentage.
More complex options for reducing the results of ranking and pairwise comparison of subjects to a one-dimensional criterion indicator associated with the use of computer algorithms for multidimensional scaling. Metric and non-metric methods of multidimensional scaling are presented in sufficient detail in / Ayvazyan S. A., et al., 1989 /. It also contains references to literature for more detailed acquaintance with these methods.
In practice, the experimental criteria for external information content have become much more common. This is mainly due to the difficulty of organizing examinations and using the usual quantitative methods for measuring the required quality. The experimental criteria are the results of a simultaneous and independent examination of the subjects by another test, which is considered to be approved and presumably measures the same property as the designed test. Naturally, simply constructing a duplicate test makes sense if you need to create a parallel form. Such an approach is most appropriate when the goal is to improve the actual diagnostic and operational characteristics of the well-known psychodiagnostic tools.
As life criteria, they use objective socio-demographic and biographical data (length of service, education, profession, admission or dismissal), performance indicators, production performance indicators for the performance of certain types of professional activity (drawing, modeling, music, storytelling, etc. .). These criteria are most often used to construct tests of ability to learn, achievements in individual disciplines, intelligence, methods for professional selection and vocational guidance, tests of general and special abilities, etc. The external criterion can be represented by a nominal, ranking or quantitative indicator, "tied" to the objects analyzed TED. This indicator will be denoted z later. The specificity of z affects the choice of method for determining the parameters of the diagnostic model.
From the standpoint of regression analysis, the criterion indicator z is considered as a “dependent” variable (usually rank or quantitative), which is expressed by a function of the “independent” attributes xi, ..., xp. To assess the effectiveness of the regression diagnostic model, a residual vector ε = (ε1, ..., εn) 'is introduced, which reflects the effect on z of the totality of unaccounted random factors or the measure of achievable approximation of the values of the criterion index zi by functions of type y (хi). The linear regression function is written as follows.
zi = wo + w'xi + εi
w0 is called the free term, and the elements of the weight vector w = (w1 ..., wр) are called regression coefficients.
There are two approaches, depending on the origin of the data matrix. In the first, it is considered that the signs xj are deterministic and the random variable is only the dependent variable (criterion indicator) z. This model is used most often and is called a model with a fixed data matrix. In the second approach, it is considered that the signs x1, ..., xр and z are random variables with a joint distribution. In such a situation, the evaluation of the regression equation is an estimate of the conditional expectation of the random variable z, depending on the random variables xi, ..., xp / Anderson T., 1963 /. This model is called a model with a random data matrix / Enukov I. S., 1986 /. Each of these approaches has its own characteristics. At the same time, it is shown that models with a fixed data matrix and a random data matrix differ only in the statistical properties of the estimates of the parameters of the regression equation, whereas the computational aspects of these models coincide / Demidenko E. 3., 1981 /. In the equation of a linear regression function, it is usually assumed that the values of εi (i = 1, N) are independent and randomly distributed with zero mean and variance σ2ε, and the parameters w0 and w are estimated using the least squares method (OLS). The minimum sum of squared residuals is sought.
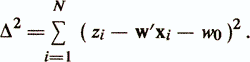
This leads to a normal system of linear equations:
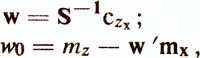
where czx is the vector of covariance estimates between the criterion index z and the characteristics x1, ..., xp; mz is the mean value of z; mx and S are the vector of averages and the covariance matrix of attributes xi, ..., xp. The main indicators of the quality of the regression diagnostic model are as follows / Enukov I.S., 1986 /: - residual sum of squares
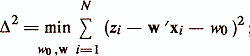
- unbiased error variance estimate
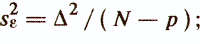
- estimation of the variance of the predicted variable
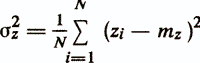
- coefficient of determination
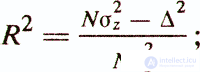
- estimate of the variance of the regression coefficients
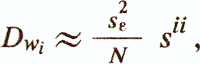
where sii is the corresponding element S -1;
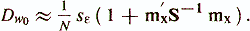
Of particular note is the above coefficient of determination R2. It is the square of the correlation coefficient between the values of the criterion variable z and the values calculated using the model y (x) = w'x + w0 (the square of the multiple correlation coefficient). The statistical meaning of the coefficient of determination is that it shows how much of the dependent variable z is explained by the constructed regression function y (x). For example, with a coefficient of determination of 0.49, the regression model explains 49% of the variance of the criterion indicator, while the remaining 51% are considered to be due to factors not reflected in the model.
Another important indicator of the quality of a regression model is statistics
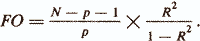
Using this statistic, the hypothesis Н0: w1 = w2 = = ... = wp = 0 is tested, that is, the hypothesis that the combination of signs xi, ..., xp does not improve the description of the criterion indicator compared to the trivial description zi = mz . If FO> fp, Np-1, where fp, Np-1 is a random variable with F-distribution with p and Npl degrees of freedom, then H0 is rejected (Fisher criterion).
In the regression analysis, another hypothesis about the equality to zero of each of the regression coefficients separately H0: wi = 0 is often checked. To do this, calculate the P-value of P (| tN-p |> ti}, where ti = wi / √Dwi, and the value tN-p has a t-distribution with (N-p) degrees of freedom. Here it should be emphasized that the adoption of Ho (high P-value) does not mean that the considered attribute xi should be excluded from the model. This cannot be done, since a judgment about the value of this characteristic can be made based on the analysis of the cumulative interaction in the model of all signs. Therefore, a high p-value serves only a “signal” about a possible non-informativeness of one or another sign.
Описанная выше технология оценки параметров линейной диагностической модели относится к одной из классических схем проведения регрессионного анализа. Известно большое количество других вариантов такого анализа, опирающихся на различные допущения о структуре экспериментальных данных и свойствах линейной модели (например, Демиденко Е. 3., 1982; Дрейпер Н. и др., 1973; Мостеллер Ф. и др., 1982). Однако в практике конструирования психодиагностических тестов применение классических схем регрессионного анализа с развитым математическим аппаратом оценки параметров регрессионной модели часто вызывает большие сложности. Причин указанных сложностей немного, но они весьма весомы.
Во-первых, сюда относится специфический характер исходных психодиагностических признаков и критериального показателя, которые, как правило, измеряются в дихотомических и ординальных шкалах. Меры связи таких признаков, как указывалось выше, имеют несколько отличную от коэффициента корреляции количественных признаков трактовку и сравнительно трудно сопоставимое поведение внутри интервала [0,1]. Поэтому расчетные формулы регрессионного анализа, полученные для количественных переменных, приобретают значительную степень приблизительности.
Во-вторых, число исходных признаков, подвергающихся эмпирико-статистическому анализу в психодиагностических исследованиях, велико (может достигать несколько сотен) и между ними, как правило, встречаются объемные группы сильно связанных признаков. В этих условиях возникает явление мультиколлинеарности, приводящее к плохой обусловленности и в предельном случае вырожденности матрицы ковариации S . При плохой обусловленности S решение системы является неустойчивым — норма вектора оценок коэффициентов регрессии и отдельные компоненты w могут стать весьма большими, в то время как, например, знаки коэффициентов wi могут инвертироваться при малом изменении исходных данных /Демиденко Е. 3., 1982; Айвазян С. А. и др., 1985/.
Указанные обстоятельства, ряд которых можно продолжить, обусловили приоритет в психодиагностике «грубых» методов построения регрессионных моделей. В основном проблема оценки параметров линейной психодиагностической модели сведена к задаче отбора существенных признаков.
There are many approaches to solving the problem of determining the group of informative features: consideration of all possible combinations of features; the “k” method of the best signs / Barabash B. A., 1964; Zagoruiko N. G., 1964 /; methods of successively reducing and increasing the group of characters / Marill T. et al., 1963 /; generalized algorithm "plus l minus r " / Kittrer J., 1978 /; methods based on maxmin strategy / Backer E. et al., 1911 /; evolutionary algorithms, in particular, random search algorithms with adaptation / Lbov G. S., 1965 /; branch and bound method / Narendra PM et al., 1976 / and others.
Significant computational difficulties associated with the high dimensionality of the space of the original features led to the fact that in the practice of constructing psychodiagnostic tests, the simplest algorithms for determining the composition of a linear regression model are used.
The basis of this method is the assumption of the statistical independence of the analyzed signs. If the coefficient of determination R2 is used as a criterion for the effectiveness of a linear diagnostic model, then its correlation coefficient with the criterion indicator r (xi, z) can serve as a measure of the information content of an individual trait (depending on the type of initial signs and the scale in which the criterion indicator is measured, appropriate communication measures are used). The initial set of attributes xi ...., xp is ordered modulo the correlation coefficient
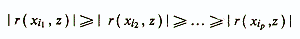
and the “k” of the first, most valuable attributes is selected from the constructed series.
The more strictly the condition of independence of the selected features is observed, the better the final result will be. In / General Psychodiagnosis ..., 1987 / the following illustration is given by X. Garrett of the efficiency of the algorithm, which allows to select the optimal set of test items. Suppose there are 20 points, each of which has a correlation with an external criterion of about 0.30. If these points correlate with each other at the level of r (xi, xj) = 0.60, then the multiple correlation coefficient of the linear diagnostic model is 0.38, but if r (xi, xj) = 0.30, the multiple correlation rises to 0 52 Finally, with r (xi, xj) = 0.10, the efficiency of the test reaches a high value of 0.79. This fact is well researched in the theory of regression analysis (for example, Hey J., 1987). It is also quite understandable at the qualitative level of reasoning, since a strong dependence of symptoms means duplication of a large part of information about the manifestation of the diagnosed property in the objects under study. use more complex methods of analyzing experimental information.
Depending on the criterion of optimality of the group of signs, various variants of the PUVG algorithm are possible. The most commonly used option is based on the analysis of partial correlations between the external criterion and test items. The PUVG algorithm is as follows.
Step 1. From the set of initial characteristics xi, ..., xp, the variable xi1 is selected, which has the maximum value of the square of the pair-correlation coefficient with the criterion index r2 (xi1, z). Symptom xi1 is the initial set of diagnostic variables X (1).
Step 2. Let an informative set of j attributes X (j) = xi1, ..., xij be already constructed. The sign xij + 1 is searched from the condition
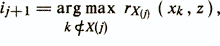
where rХ (j) (xk, z) is the partial correlation coefficient between xk and z with fixed values of variables from X (j). In addition, the condition of linear independence of the xk attribute from the set of X (j) features is checked, which provides the computational stability of the algorithm,
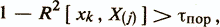
where R2 [xk, X (j)] is the square of the multiple correlation coefficient of the set X (j) with the checked attribute xk
τthor - given small positive value. After determining the variable xij + 1, the conditions of the shutdown of the HSMC algorithm are checked. Perhaps one of the following stopping conditions / Enukov I.S., 1986 /.
- The specified number of signs of p3 is reached, that is, j + 1 = p3. - The hypothesis is tested that the maximum in absolute value of the partial correlation coefficient from the p — j coefficients of the partial correlation of features that are not in X (j) is zero. If this hypothesis is confirmed, then the set of signs is considered final.
- The maximum value of the Fo-statistic has been reached for assessing the quality of the regression equation, which is determined by the formula for calculating Fo. If none of the conditions is fulfilled, then the xij + 1 attribute joins the set X (j) and returns to step 2. After the algorithm stops, weights can be assigned to each of the signs included in the informative group, expressing the contribution of each attribute to criterion not reducible to the contribution of other signs / Avanesov V.S., 1982 /.
Despite the more sophisticated operations with experimental information in comparison with the best feature “k” method, the method of IBCG is largely heuristic. It does not guarantee obtaining an optimal result, which can be achieved with the help of a complete enumeration of all possible combinations of the original features. The deviation from the optimal solution is probably already at the first step of the algorithm of the HFVG when the initial diagnostic sign is selected from the informative group. Although this feature has a maximum correlation with the criterion index, this does not mean that it would necessarily be included in the group of informative features if any other feature was chosen as the initial one.
It does not guarantee obtaining an optimal result and the method of successive reduction of the group of signs of the PUMG, in which the initial regression equation is constructed for the full set of initial signs. From this complete equation, one variable is then successively removed, and for the remaining signs, the value of the coefficient of determination R2 or some other integral indicator of the quality of the regression function is calculated. The PUMG algorithm stops when further simplification of the regression equation begins to degrade its quality. Using this algorithm, more effective results can be obtained than for PUVG, in the case of a relatively small volume of the group of initial features. For high dimensions of the original feature space (and when constructing psychodiagnostic tests, the dimension reaches tens and even hundreds), serious problems arise in evaluating the quality indicator of the regression equation, since the effect of a single attribute on the total effect of the diagnostic model becomes comparable to its measurement error.
The generalization of PUVG and PUGG is the “plus l minus r ” method, which, as its name implies, alternately works on addition, then on exclusion of signs into the regression equation. In general, it can be noted that all the mentioned methods for determining the composition of signs in the regression equation contain in one way or another a heuristic component. In each case, it is difficult to predict in advance which of these methods will lead to more optimal results. Therefore, in practice, attempts to approach the desired optimum are always associated with the combined use of various search algorithms for a group of informative features in a diagnostic regression model.
If the criterion indicator z is measured on a nominal scale, or the relationship of this indicator with the original characteristics is non-linear and unknown, then discriminant analysis methods are used to determine the parameters of the diagnostic model. In this case, the subjects, the results of which are presented in the TED, are divided into groups (classes) in accordance with the external criterion, and the effectiveness of the diagnostic model is examined from the point of view of its ability to divide (discriminate) the diagnosed classes.
A large group of discriminant analysis methods is in one way or another based on the Bayesian decision-making scheme about the belonging of objects to diagnostic classes. The Bayesian approach is based on the assumption that the problem is formulated in terms of probability theory and all quantities of interest are known: a priori probabilities P (ωi) for classes ωi (i = 1, K) and conditional densities of values of the feature vector P (x / ωi). Bayes Rule is to find the posterior probability P (ωi / x), which is calculated as follows
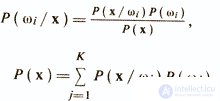
The decision on the belonging of an object xk to the class ωj is made when the condition is met that ensures a minimum of the average probability of classification error.
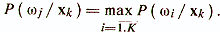
If two diagnostic classes ω1 and ω2 are considered, then in accordance with this rule, the decision ω1 is made at Р (ω1 / х)> Р (ω2 / х) and ω2 at P (ω2 / x)> Р (ω1 / x). The value of P (ωi / x) in the Bayes rule is often called the likelihood ωi for a given x and the decision is made through the likelihood ratio or through its logarithm
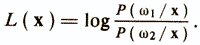
For dichotomous features, which in many cases have to deal with when constructing psychodiagnostic tests, the p-dimensional vector of attributes x can take one of n = 2p discrete values of v1, ..., vn. The density function P (x / ωi) becomes singular and is replaced by P (vk / ωi) - the conditional probability that x = vk under the condition of the class ωi.
In practice, in the discrete case, as in the continuous case, when the number of initial signs xi is large, the definition of conditional probabilities encounters considerable difficulties and often cannot be carried out. This is connected, on the one hand, with the unreality of even a simple viewing of all points of the discrete space of dichotomous signs. So, for example, if we use the initial criteria for constructing a diagnostic rule for the approval of the MMPI test questionnaire, then p = 550 and thus n = 2550. On the other hand, even with a much smaller number of signs, for a reliable assessment of conditional probabilities, it is necessary to have the results of a survey of a very large number of subjects.
A common technique for overcoming these difficulties is a model based on the assumption of independence of the initial dichotomous features. Let, for definiteness, the components of the vector x take the values 1 or 0. Denote pi = P (xi = 1 / ωi) - the probability that xi is 1 if the objects are extracted from the diagnostic class ω1, and qi = P (xi = 1 / (ω2) is the probability of equality for 1 of the attribute xi in the class ω2. In the case of pi> qi, one should expect that the z-th attribute will more often take the value 1 in the class of ω1 than in ω2. Assuming independence of the signs, P (x / ωi) as a product of probabilities
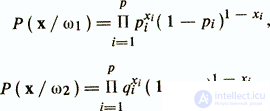
The logarithm of the likelihood ratio in this case is determined as follows.
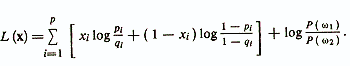
It can be seen that this equation is linear with respect to signs xi. Therefore, you can write
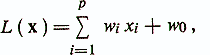
where are the weights
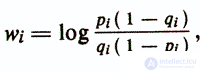
and the threshold value
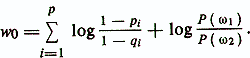
If L (xk)> 0, then the decision is made whether the object xk belongs to the diagnostic class ω1, and if L (xk) <0, then ω2.
The result is similar to the above three-day regression analysis for independent traits. The values of pi and qi can be expressed using the notation adopted for the elements of the conjugacy table of dichotomous features (see Table 2). Here, the diagnostic class index ωi will be one of the two dichotomous features. Substituting these notation in logarithm, we obtain wi = log (bc / ad). That is, an expression for calculating the weight coefficients in the Bayesian decision function for independent attributes gives wi values monotonically related to the Pearson coefficient φ, which in some cases can be used to determine the coefficients of a linear regression equation.
The results of the discriminant and regression analysis for the case of the two classes largely coincide. The differences stem mainly from the use of different criteria for the effectiveness of the diagnostic model. If the integral indicator of the quality of a regression equation is the square of the coefficient of multiple correlation with an external criterion, then in the discriminant analysis this indicator is usually formulated regarding the probability of an erroneous classification (FOC) of the objects under study. In turn, to uncover the relationship of the wok with the structure of the experimental data in the discriminant analysis are widely used geometric ideas about the division of diagnosable classes in the space of signs. We use these representations to describe other, non-Bayesian, discriminant analysis approaches.
The set of objects belonging to the same class ωi forms a “cloud” in the r-dimensional space Rp, given by the source features. For successful classification it is necessary that / Enukov I. S., 1986 /:
a) the cloud of ωi was mainly concentrated in a certain region Di of the space Rp;
b) an insignificant part of the “clouds” of objects corresponding to the other classes hit the Di area.
The construction of a decision rule can be considered as a search problem for K non-intersecting domains Di (i = l, K) satisfying conditions a) and b). Discriminant functions (DF) define these regions by defining their boundaries in the multidimensional space Rp. If the object χ falls into the domain Di, then we will assume that a decision is made on whether the object belongs to ωi. Let P (ωi / ωj) be the probability that an object from the class ωj erroneously falls into the domain Di, corresponding to the class ωi. Then the criterion for the correct determination of areas A is
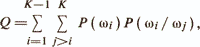
where P (ωi is the a priori probability of an object from ωi. The criterion Q is called the criterion of the average probability of an erroneous classification. Minimum Q is achieved by using, in particular, the above Bayesian approach, which, however, can be practically realized only with the validity of a very strong assumption independence of the original features in this case provides an optimal linear diagnostic model. A large number of other approaches also use linear discriminant functions, but at the same time round less strict restrictions are imposed data. Consider the basic of these approaches.
For the case of two classes ω1 and ω2, methods for constructing a linear discriminant function (LDF) are based on two assumptions. The first is that the regions D1 and D2, in which objects from the diagnosed classes ω1 and ω2 are concentrated, can be separated by a (p-1) -dimensional hyperplane y (x) + wo = w1x1 + w2x2 + ... + wpxp + w0 = 0 In this case, the coefficients wi are interpreted as parameters characterizing the slope of the hyperplane to the coordinate axes, and wo is called the threshold and corresponds to the distance from the hyperplane to the origin. The preferential location of objects of one class, for example ω1, on one side of the hyperplane is expressed in the fact that for them, for the most part, the condition y (x) <0 will hold, and for objects of another class ω2 - the opposite condition y (x)> 0. The second assumption concerns the quality criterion of the separation of the regions D1 and D2 by the hyperplane y (x) + wo = 0. Most often it is assumed that the separation will be the better, the further apart are the average values of random variables m1 = Е {y (x)}, x є ω1 and m2 = E {y (x)}, x є ω2 where E { •} - averaging operator.
In the simplest case, it is assumed that the classes ω1 and ω2 have the same covariance matrices S1 = S2 = S. Then the vector of optimal weight coefficients w is defined as follows / Anderson T., 1963 /
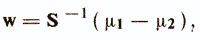
where μi is the vector of average values of attributes for the class ωi. Weights provide maximum criteria
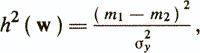
where σ2у is the variance y (x), assumed to be the same for both classes. The maximum value of h2 (w) is called the Mahalanobis distance between the classes ω1 and ω2 and is equal to
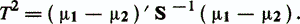
To determine the magnitude of the threshold, wo introduce an assumption about the form of the laws of distribution of objects. If objects of each class have a multidimensional normal distribution with the same covariance matrix S and vectors of mean values μi, then the threshold value wo minimizing the Q criterion will be
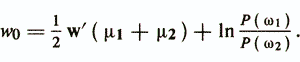
The following statement about LDF optimality is true: if objects from ωi (i = l, 2) are distributed according to a multidimensional normal law with the same covariance matrix, then the decision rule w'x> w0 , the parameters of which are determined, is the best in the sense of the average likelihood classification error criterion .
For the case when the number of classes is more than two (K> 2), K is usually determined by the discriminant weight vectors (directions)
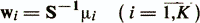
and thresholds
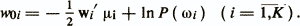
An object x belongs to the class ωi if the condition
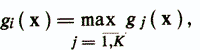
where gj (x) = wj '/ x — woj.
The formulas for calculating the threshold values of wo and woi include the values of a priori probabilities P (ωi). The a priori probability P (ωi) corresponds to the fraction of objects belonging to the class ωi in a large series of observations carried out under certain stationary conditions. Usually P (ωi) are unknown. Therefore, when solving practical problems, without changing the discriminant weight vectors, these values are set on the basis of the subjective assessments of the researcher. It is also often assumed that these values are equal or proportional to the volumes of training samples from the diagnostic classes under consideration. Another approach to determining the parameters of linear discriminant functions uses as a criterion the ratio of the intraclass dispersion of the projections of objects in the direction y (x) = w'x with the total dispersion of the projections of the combined sample. The same assumptions are usually used as in the previous case. Namely, the classes ωi (i = l, K) are represented by sets of objects normally distributed in the p-space with the same covariance matrices S and vectors of mean values μi. Denote C - the covariance matrix of the combined set of volume objects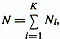 
, μ0 is the vector of averages of this population. The expression C through S is given by the following formula:
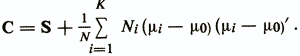
The variance of the projections of the entire set of objects in the direction y (x) will be c2у = w'Cw , and the intraclass dispersion will be S2y = w'Sw . Thus, the optimality criterion of the chosen direction y (x) for the separation of the classes ωi is written in the following form:
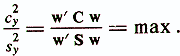
This ratio shows how many times the total variance, which is caused by both the intraclass variation and the differences between classes, is greater than the variance, due only to the intraclass variation. The weight vector w, satisfying this equation, based on the previously considered geometric interpretation of the linear diagnostic model, specifies a new coordinate axis in the p-dimensional space y (x) = w'x (|| w || = 1) with the maximum inhomogeneity of the studied set of objects . The new variable y (x) = w'x corresponds, no-essentially, the first main component of the combined set of objects, obtained with regard to the additional training information about the belonging of objects to the diagnostic classes ωi. The weight vector w at which the maximum value of the optimality criterion of the chosen direction is reached is determined by solving a generalized eigenvalue problem
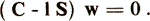
There are a total of p eigenvectors satisfying the above equation. These vectors are ordered by the magnitude of the eigenvalues l1> l2> ...> lp and get the system of orthogonal canonical directions w1, ..., wp.
Minimum relationship value
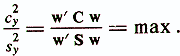
equal to 1 and means that for the chosen direction w the entire available variation of the variable y (x) is explained only by the intraclass spread and does not carry any information about the difference between the classes ωi. For the case K = 2, the estimate of the weight discriminant vector wF = S-1 (μ1-μ2) is an eigenvector for (C-1S) w = 0 with the eigenvalue lF = T2 + 1. Any vector orthogonal to wF will also be a solution (C-1S) w = 0 with an eigenvalue equal to one. Therefore, to answer the question, what number of n
2, in order not to lose information about interclass differences, test the hypothesis Ho about equality to the unit of the last pn of eigenvalues. The procedure for such verification is set forth, for example, in / Enukov I. S., 1986 /. Some other aspects of discriminant analysis are also considered in sufficient detail for practical application.
The above methods for determining discriminant weight vectors lead to optimal results if sufficiently stringent conditions for the normal distribution of objects within the classes and the equality of the covariance matrices Si are observed. In the practice of psychodiagnostic studies these conditions, as a rule. not performed. But the deviations of the real distributions of objects from the normal and the differences in covariance matrices, which in some cases are well studied theoretically, are not the main reasons for the limited use of the classical formulas of discriminant analysis. Here, as in the construction of regression psychodiagnostic models, the qualitative and dichotomous nature of the signs, their large number and the presence of groups of related signs determine the use of “coarse” algorithms for finding discriminant functions. These algorithms are also mainly reduced to the selection of informative features using heuristic procedures k - the best features and the successive increase and decrease of the group of features. The difference between these procedures lies in different criteria for optimality of features than in the construction of regression models. Such criteria in the discriminant analysis are formulated with respect to the average probability of an erroneous classification and often a measure of the informativeness of a trait when it is added to a group of features or excluded from a group that does not depend on the size of the group, serves / Enyukov I. S., 1986 /
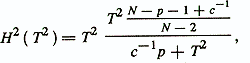
where T2 is the Mahalanobis distance between the two diagnosed classes ω1 and ω2; s-1 = N1-1 + N2-1, In general, it can be concluded that for the two classes the discriminant analysis methods are in many respects similar to the regression analysis methods. An extension to the regression scheme in the discriminant analysis is the idea of the separating boundaries of the diagnosed classes, which can lead to more sophisticated forms of these boundaries and procedures for finding them.
Publications devoted to the typological approach are usually considered within the framework of psycho-prediction (for example, Yampolsky L. T., 1986; Kulagin B. V. and others., 1989). The point of view that divides psychosocial and psychodiagnostics is known / Zabrodin Yu. M., 1984 /. At the same time, from the position of the formal mathematical apparatus, psychoprognostics and psychodiagnostics have much in common. In either case, the subject is described by a set of numbers (by the r-dimensional vector of signs), in the same way, each subject is assigned the value of a certain criterial indicator z, and the task is to build a mathematical model that has the maximum correlation with z or discriminating subjects like z. Of course, the longer the time interval over which the forecast applies, the more serious difficulties the researcher encounters in determining the criterion indicator and the more difficult the structure of the model may be y = y ( x). But, one way or another, this presentation will not draw the line between the concepts of psycho-prediction and psycho-diagnostics, but will focus mainly on the phenomenology of the experimental data processing procedure, which is called the typological approach.
The expediency of applying the typological approach is due to the insufficient efficiency of linear diagnostic models. So, L. T. Yampolsky / 1986 / notes that this is the simplest way to integrate individual factors into real behavior and that psychological factors (initial signs in a diagnostic model. - VD) can interact in a more complex way. B / Kulagin B.V. et al., 1989 / examines the problems of constructing diagnostic models for the purpose of occupational selection and indicates that, as a rule, the aggregate of the examined candidates is idealized as a homogeneous sample from a certain general population and the model for predicting the success of a professional activity turns out to be averaged for all the subjects included in the survey. This leads to a decrease in the proportion of forecast coincidence with real professional success, which in this case almost never exceeds 70-80%. Further, the reasoning of the above authors, although somewhat different, leads to the same conclusions. These arguments are approximately as follows.
In conditions of heterogeneity of the training set, linear diagnostic models should be replaced by non-linear ones. However, the solution to the problem of constructing nonlinear models is difficult because of the lack of a priori information about the type of the desired functions y = y (x). In such cases, an effective result can be achieved using the piecewise linear approximation methods y = y ( x). In turn, the success of the piecewise linear approximation depends on how well the test subjects can be divided into homogeneous groups, each of which is individually constructed its own linear diagnostic model. Это можно рассматривать как индивидуализацию диагностического правила, которая заключается в выборе одной из нескольких функций у=у (х) для каждого испытуемого с учетом его принадлежности той или иной группе.
Таким образом, процедура построения диагностической модели состоит из двух этапов. На первом этапе производится разбиение всего множества испытуемых X={хi}, i=1,N на М однородных групп Gj( X= UGj ) , j= 1,M На втором этапе для каждой группы Gj вырабатывается линейное диагностическое правило yj=yj( х) с помощью рассмотренных выше методов линейного регрессионного или дискриминантного анализа. Соответственно процедура собственно диагностики также осуществляется в два приема. Сначала определяется принадлежность испытуемого хi к одной из ранее выделенных групп Gj и затем для диагностики хi применяется требуемая диагностическая модель yj = yj( х).
«Слабое звено» данного подхода заключается в трудно формализуемом и нечетком определении понятия однородности группы объектов. Как известно, задаче разбиения объектов на однородные группы уделяется значительное место в общей проблематике анализа данных. Методы решения этой задачи носят разные названия: автоматическая классификация, распознавание без учителя, таксономия, кластерный анализ, расщепление смеси и т. д., но имеют одинаковую сущность. Все они в явной или неявной форме опираются на категорию близости (различия) объектов в пространстве признаков. Для решения задачи выделения однородных групп объектов исследования необходимо дать ответы на три основных вопроса:
а) какие признаки будут считаться существенными для описания объектов?
б) какая мера будет применяться для измерения близости объектов в пространстве признаков?
в) какой будет выбран критерий качества разбиения объектов на однородные группы?
На каждый из приведенных вопросов существует много вариантов ответов, и в зависимости от выбранного ответа можно получить совершенно различные разбиения объектов на однородные группы. Поэтому решение конкретной задачи выделения однородных групп объектов всегда не лишено субъективной оценки исследователя. В следующей главе будут более подробно рассмотрены возможные алгоритмы разбиения множества объектов на группы в рамках общей проблемы анализа многомерной структуры экспериментальных данных. Здесь же ограничимся рекомендациями, изложенными в /Ямпольский Л. Т., 1986; Кулагин Б. В. и др., 1989/, полезность которых подтверждена значимыми практическими результатами.
В работе /Кулагин Б. В. и др., 1989/ рекомендуется для группирования испытуемых отбирать признаки, хорошо дискриминирующие массив исходных данных и слабо коррелирующие между собой. Кроме того, набор этих признаков должен быть минимизирован. Л. Т. Ямпольский /1986/ предлагает выделять группировки объектов в
продолжение следует...
Часть 1 Designing psychodiagnostic tests: traditional mathematical models and algorithms
Часть 2 Contrast group method - Designing psychodiagnostic tests: traditional mathematical models
Часть 3 6. Standardization and testing of diagnostic models - Designing psychodiagnostic
Часть 4 - Designing psychodiagnostic tests: traditional mathematical models and algorithms
Comments
To leave a comment
Mathematical Methods in Psychology
Terms: Mathematical Methods in Psychology