Lecture
Let the PDK set on the plane. Take an arbitrary point P (x, y) on the plane. The location of the point P on the plane is uniquely determined by the Cartesian coordinates x and y . Also, the position of point P on the plane can be uniquely determined by the module of the radius vector of point P and the angle formed by the vector 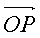 and the Ox axis (Fig. 4).
and the Ox axis (Fig. 4).
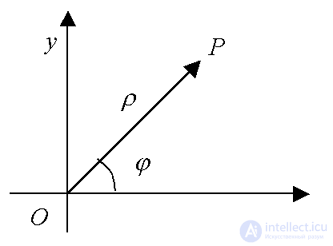
Fig. four
Denote by ρ the module of the radius-vector 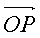 through φ is the angle between the vector
through φ is the angle between the vector 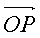 and axis Ox . The values of ρ and φ can be taken as the new coordinates of the point P : P ( ρ, φ ) . These coordinates are called polar coordinates . Cartesian coordinates are expressed in polar terms as follows:
and axis Ox . The values of ρ and φ can be taken as the new coordinates of the point P : P ( ρ, φ ) . These coordinates are called polar coordinates . Cartesian coordinates are expressed in polar terms as follows:
Comments
To leave a comment
Linear Algebra and Analytical Geometry
Terms: Linear Algebra and Analytical Geometry