3.1. Definition of a rectangular Cartesian coordinate system

A rectangular Cartesian coordinate system (PDK) consists of a fixed point O (the center of the coordinate system ) and three intersecting in it, mutually perpendicular direction lines O _x , O _y , O _z ( axes of the coordinate system ). Directions are chosen so that the straight lines form the right three vectors.

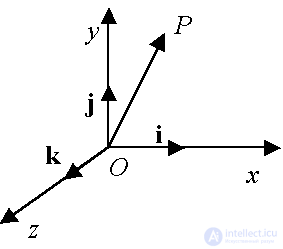
Fig. 2

The unit vectors defining the directions of the axes O _x , O _y , O _z are denoted by the letters i, j, k and form an orthonormal basis (Fig. 2).

Vector 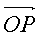called the radius vector of a point 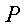. Vector coordinates 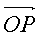relative to the base i, j, k are coordinates of the point 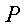i.e. if a 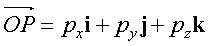( 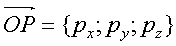), then 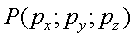- point with coordinates p _x , p _y , p _z .

Because 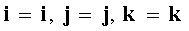then .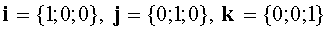

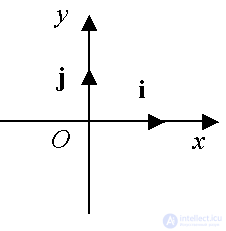
Fig. 3

If vectors are viewed on a plane, then the PDK consists of two perpendicular axes O _x , O _y with the guide orta i, j ( i = {1; 0}, j = {0; 1}) (Fig. 3).