Lecture
George boule
All mechanisms, gears, vacuum tubes and circuit boards are all not computer yet. The developments of Pascal and Leibniz, about which we have already told you, and Babbage, whose achievements we will discuss in the next chapter, are also important. These developments required the original theory of logic in order, ultimately, to breathe life into machines that "think."
Expanding the general Leibniz method, formulated 188 years earlier, in which all the true reasons were reduced to the type of computation, the English mathematician D. Boule in 1854 laid the foundation for what we know today as mathematical logic by publishing the work Study of the Laws of Thinking.
In this work, published when he was 39 years old, Buhl reduced logic to an extremely simple type of algebra, the algebra of propositional logic, which was a system of symbols and rules applied to various objects (numbers, letters, sentences).
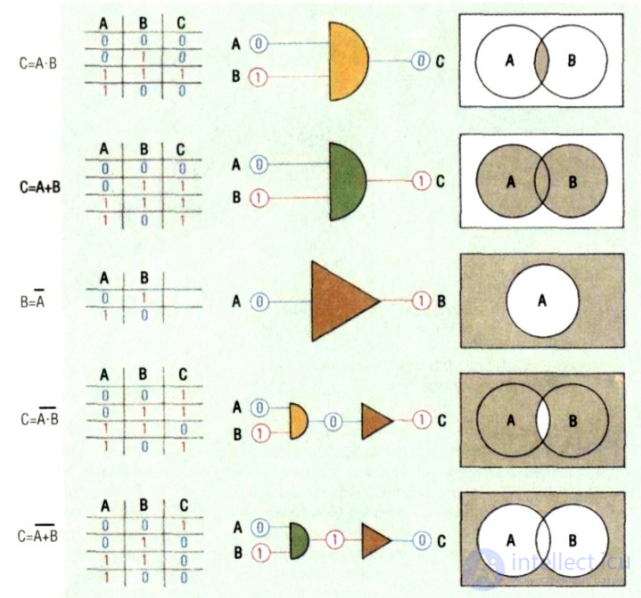
His theory of logic, based on three main actions - AND (and), OR (or), NOT (not) - was to become the basis for the development of switching telephone lines and a computer project in the XX century. Like Leibniz’s ideas, Boolean algebra was neglected for many years after it was created.
The importance of the work, recognized by Logic de Morgan, a contemporary of Boole, was as follows: “Symbolic processes of algebra, created as tools of numerical calculation, competently express every law of thought and possess grammar and vocabulary of everything that contains a system of logic. We didn’t anticipate this until it was proven in the “Laws of Thinking”. "
George Boole was born on November 2, 1815 in Lincoln (England), in the family of a poor shoemaker. Although he was a contemporary of C. Babbage, he did not come from a privileged class like Babbage.
Coming from a stratum of society, whose children were actually deprived of attending university, George had to study on his own. Although the industrial revolution had already taken place in England, knowledge of ancient languages was an indicator of the level of education of a gentleman. Of course, no Latin or Greek was taught at the school that Buhl attended. Buhl himself studied Greek and Latin, with the support of a poorly educated father, and at the age of 12 he was able to translate Horeis's ode into English. Not understanding anything about the quality of the translation technique, Buhl’s proud father nevertheless published it in a local newspaper. Some experts stated that the 12-year-old boy could not make such a translation, others noted serious technical defects in the translation. Having decided to improve his knowledge of Latin and Greek, Buhl spent the next two years in a serious study of these languages, and again without any help. Although this knowledge was not enough to turn into a true gentleman, such hard work disciplined him and contributed to the classical style of matured Boolean prose.
It is known that his father left school after three years of study, and at the same time it is surprising that Buhl received an early mathematical education from his father, who was self-taught in this field.
At the age of 16, it became necessary for Buhl to start a working life in order to help his parents. Having received the work of a “junior teacher,” or an assistant teacher in an elementary school, Buhl had to spend 4 years teaching in two different schools.
Always thinking about the perspective of his place in life, Buhl began to consider several paths open to him. His initial teaching was always at the level, but he did not consider it a profession, although it was honorable. Boole became a clergyman.
When he did not teach, he spent time in serious study of French, German and Italian, in preparation for church life. Failures, the poverty of his family once again destroyed the plans of Buhl; parents urged him to abandon religious life because of their deteriorating financial situation.
Responsive, as always, to the advice of parents, Buhl decided to open his own school. He was 20 years old. Teaching, Buhl considered himself a student and began to study the full course of higher mathematics. He studied Newton's “Mathematical Principles”, Lagrange's “Analytical Mechanics”, the works of Laplace and other authors.
Buhl began his mathematical studies with the development of operator methods of analysis and the theory of differential equations, and then, like De Morgan, with whom he had become friends, engaged in mathematical logic.
In his first major work, Mathematical Analysis of Logic, which is an experience in calculating deductive reasoning of 1847, Boole clearly showed the so-called quantitative interpretation of the objects of logic and the need for a new approach to solving logic problems. This approach required changes and extensions of the symbolic language of algebra: the choice of symbols, operations and laws defining these operations and reflecting the specifics of the objects of study - that is, essentially creating a new calculus. Boule wrote: “Those who are familiar with the present state of symbolic algebra are aware that the validity of the analysis processes does not depend on the interpretation of the symbols used, but only on the laws of their combination. Each interpretation, preserving the proposed relations, is equally valid, and a similar analysis process can, therefore, with one interpretation, represent a solution to an issue related to the properties of numbers, with another, a solution to a geometric problem and a third solution to a problem of dynamics or statics. It is necessary to emphasize the fundamental nature of this principle. ” With the publication of "Mathematical Analysis ..." the views and brilliant intuition of this quiet, simple man became clear to his friends - mathematicians, who advised him to enter Cambridge, in order to get a generally accepted mathematical education.
Buhl reluctantly rejected these proposals because his relatives existed fully on his earnings. Without complaining about the characteristics of his teaching from time to time, Buhl finally got a short break in 1849, when he was appointed professor of mathematics at the newly opened Royal College I.
This assignment allowed him to devote more time to the “Laws of Thinking ...” - his second major work, which he continuously honed and refined for another 5 years, before publication in 1854. As Buhl wrote in the first paragraph of the book: “The purpose of this treatise:
And further: “Now, in fact, the research on the following pages shows logic, in practical terms, as a system of processes carried out with the help of symbols that have a certain interpretation and are subject to laws based on this single interpretation. But at the same time, they show these laws as identical in form with the laws of the general symbols of algebra, with one single addition, viz. ”
In other words, in general algebra it does not hold, for example: that each x is identically equal to its square — but this is true in Boolean algebra. According to Boole, x2 = x for any x in his system. In a numerical system, this equation has a unique solution “O” and “1 ″. This is the importance of the binary system for modern computers, the logical parts of which effectively implement binary operations.
In addition to logic, Boolean algebra has two other important applications. Boolean algebra is used in natural algebra. Taking into account also the idea of the “number of elements” in a set, Boolean algebra became the basis for the theory of probability.
Despite the great importance of Boolean algebra in many other areas of mathematics, the extraordinary work of Buhl was considered an oddity for many years. Like Babbage, Boole was a man ahead of his time. This happened earlier than Alfred Whitehead and Bertrand Russell published their three-volume book, Principles of Mathematics (1910-1913), which dealt with questions of formal logic.
It is worthy of attention that the mathematical discoveries that appeared in England, including the ideas of Babbage, partially relied on Buhl's achievements. Mathematicians drew attention to the idea of Babbage about the mathematical operations and values used in them. The idea was made possible by a group of British experts in the field of algebra, to which Boule belonged.
Boule demonstrated, “that logic can be reduced to very simple algebraic systems, after which it became possible for Babbage and his followers to create mechanical devices that could solve the necessary logical problems.
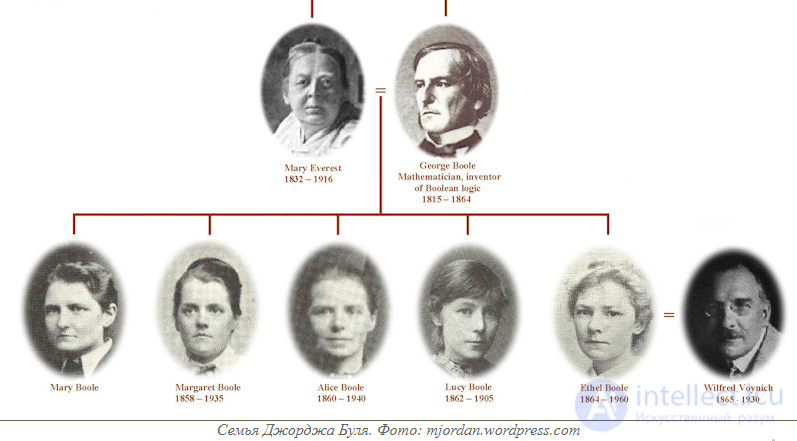
A year after the publication of the “Laws of Thinking ...” Buhl married Mary Everest, the niece of the Greek College professor at King’s College. The happy marriage lasted for nine years, until the untimely death of George Boole. On December 8, 1864, at the age of 49, revered and famous, he died of pneumonia.
Boule was a consistent and disciplined man, however, he widely demonstrated his own vision of the world in his statements. This powerful combination of intellect and intuition in George Boole embodied in various mathematical ideas. In conclusion of the essay about the father of Boolean algebra, I would like to briefly describe the Buhl family.
As already mentioned, the wife of Boole was the niece of George Everest, in 1841 he completed work on a grand scale in India.
In honor of his achievements, the highest peak of the world, Jomolungma in the Himalayas, was at one time even called Everest. Mary herself, unlike the wives of many other mathematicians, understood the scientific ideas of her husband and, with her attention and participation, encouraged him to continue her research. After his death, she wrote several essays and in the last of them, “The Philosophy and Entertainment of Algebra,” published in 1909, promoted George’s mathematical ideas.
The couple have five daughters. The eldest, Mary, married C. Hin-ton, a mathematician, inventor, and science fiction writer, author of the well-known story “The Case in Flatland,” which describes certain creatures living in a flat two-dimensional world. Of the numerous descendants of Hintons, three grandchildren became scientists: Howard, an entomologist, and William and Joan, physicists. The latter was one of the few women physicists who participated in the work on the atomic project in the United States.
The second daughter of Bulay, Margaret, went down in history as the mother of the largest English mechanic and mathematician, a foreign member of the USSR Academy of Sciences, Geoffrey Taylor. The third, Alicia, specialized in the study of multidimensional spaces and received an honorary degree from Gronin-Gene University. The fourth, Lucy, became the first female professor in England to head the department of chemistry.
But the most famous of all the daughters of Bulee was the youngest, Ethel Lilian, who married a scientist - an emigrant from Poland, Voynicha. Entering the revolutionary emigrant environment, she wrote the novel “The Gadfly”, which glorified her all over the world. He was followed by several novels and musical works, as well as an English translation of the poems of Taras Shevchenko. Voynich passed away in New York at the age of 95, a little before the centenary of the death of her famous father, the mathematician George Boole.
Comments
To leave a comment
Persons
Terms: Persons