Fuzzy logic, fuzzy sets and fuzzy calculations

Introduction

Fuzzy logic is a section of multi-valued logic (see Logic of many values), which is based on a generalization of classical logic (see Logic) and the theory of fuzzy sets proposed by the American mathematician Lutfi (Lotfi) Zadeh to formalize fuzzy knowledge characterized by linguistic uncertainty . The foundations of the theory of fuzzy sets were laid in the work of L. Zadeh “Fuzzy Sets”, published in 1965 in the journal “Information and Control” (Zadeh LA Fuzzy Sets. - Information and Control, 1965, Vol. 8, No. 3, pp. 338 –353). He also gave the name for a new field of research - “Fuzzy Logic”. The subject of fuzzy logic is the study of reasoning under conditions of fuzziness, fuzziness, uncertainty, similar to reasoning in the usual sense. Currently, fuzzy logic is widely used in computing and information systems for various purposes, since it turned out to be indispensable in cases where it is not possible to get clear answers to the questions posed or all possible situations are unknown in advance.

A fuzzy set is understood to mean a set with fuzzy boundaries, when the transition from elements belonging to the set to non-belonging to their set is not clearly defined. In classical logic, an element x from the corresponding domain belongs or does not belong to some set M. The characteristic membership function of an element in a set takes only two values: 1 when x really belongs to M , and 0 when x does not belong to M. For example: a geometrical figure either belongs to many triangles or does not belong to it. With fuzzy sets, the situation is different. Here, the element x belongs to the set A (where A is a fuzzy set) with only a certain degree, therefore the membership function of the element to the set can take any values ​​in the interval [0, 1], and not just the values ​​0 or 1.

According to L. Zadeh, the classical concept of the membership function of an element to the set is insufficient to consider situations that are described with the help of vaguely defined concepts such as “very true”, “more or less true”, “not very false” and the like. Similar linguistic meanings are represented by fuzzy sets. Here, the dichotomy of the considered membership function does not allow any element to either belong or not to belong to this set. Thus, the dichotomy of the membership function must be rejected in the same way as in the multi-valued logics the dichotomy of the function of attributing truth values ​​is rejected (the double-valued principle). Then, following the logic of L. Zadeh, the theory of fuzzy sets is based on the idea that the elements that make up a set and have a common property can have this property to different degrees and, therefore, belong to this set with different degrees. With this approach, a statement like “an element belongs to a given set A ” loses its meaning, since it should indicate with what degree the element belongs to a given set. Typically, this set of degrees of membership is evaluated on an infinite scale of real numbers from 0 to 1, that is, on the interval [0, 1], which is used as a universal set for setting the linguistic variable “truth”. In general, this allows us to determine intermediate values ​​for such generally accepted expressions as yes | no, true | false, black | white and the like. Thus, expressions of vaguely defined concepts became possible to formulate mathematically. Then, over the set of fuzzy [sub] sets, the simplest logical operations of crossing «, the union«, and the complement ¯ are determined.

In 1973, L. Zadeh introduced the concept of such a fuzzy logic, in which the set of truth values ​​is a countable set of linguistic names of truth values, understood as a linguistic variable, the values ​​of which are fuzzy sets, that is, such a variable whose values ​​are words or sentences of natural or artificial language. The set of valid values ​​for a linguistic variable is called a term set. In turn, linguistic truth values ​​have numerical values, which are already fuzzy sets, that is, the concept of truth itself is fuzzy, in contrast to classical logic, where truth can take only two values: “true” and “false”. The concept of a linguistic variable plays an important role in fuzzy inference and in decision making based on approximate reasoning.

Formally, fuzzy and linguistic variables are defined as follows.

A fuzzy variable is characterized by a triple set 〈 a , X , A 〉, where:

• a is the name of the variable;
• X is a universal set (domain of definition a );
• A is a fuzzy set on X that describes the restriction (i.e., mA ( x )) on the value of the fuzzy variable a .

The linguistic variable is characterized by a set of five 〈 b , T , X , G , M 〉, where:

• b is the name of the linguistic variable;
• T is the set of its values ​​(term-set), representing the names of fuzzy variables, the domain of definition, which is the set X. The set T is called the basic term-set of the linguistic variable;
• G is a syntactic procedure that allows you to operate with the elements of the term set T , in particular, generate new terms (values). The set T AND G ( T ), where G ( T ) is the set of generated terms, is called the extended term-set of the linguistic variable;
• M is a semantic procedure that allows you to convert the new value of the linguistic variable formed by the procedure G into a fuzzy variable, that is, to form the corresponding fuzzy set. This is evidenced by the site https://intellect.icu.

Using characters:

• the b symbol is used both for the name of the variable itself and for all its values;
• one symbol is used to indicate a fuzzy set and its name.
• Assigning multiple values ​​to symbols implies that the context is uncertain.

To date, there are two main areas of research in fuzzy logic.

The first direction includes fuzzy logic in a broad sense , which often means everything that is associated with fuzzy sets. Since the 1970s, the theory of fuzzy sets has gained considerable popularity. Since 1970, the international magazine Fuzzy Sets and Systems began to appear. Since the late 1980s, fuzzy logic has occupied one of the leading positions in information technology. Since fuzzy logic turned out to be very suitable for working with approximated information, it is used to control nonlinear systems and to simulate complex systems where ambiguities and uncertainties are generally accepted. Today, fuzzy logic is embedded in various control, information, electronic and many other systems, including artificial intelligence systems. Effective modeling of approximate reasoning has found important application for solving complex programming problems and, in general, in the technology of so-called “soft computing” (Soft Computing). To date, published literature on the issue of fuzzy sets has more than 10 thousand works.

The second direction includes fuzzy logic in the narrow sense , using methods of symbolic logic (see Symbolic logic): semantics, syntax, axiomatization, deduction, completeness, and others - both for propositional logic (see Propositional logic) and predicate logic (see The logic of predicates). In this vein, fuzzy logic is being developed as a section of multi-valued logic. This direction is a relatively young discipline exploring new logical calculus with far-reaching prospects.

The mathematical theory of fuzzy sets and fuzzy logic are generalizations of classical set theory and classical formal logic. These concepts were first proposed by the American scientist Lotfi Zadeh in 1965. The main reason for the emergence of a new theory was the presence of fuzzy and approximate reasoning when a person describes processes, systems, objects.

Before the fuzzy approach to modeling complex systems was recognized worldwide, more than a decade passed from the inception of the theory of fuzzy sets. And on this path of development of fuzzy systems, it is customary to distinguish three periods.

The first period (late 60s – early 70s) is characterized by the development of the theoretical apparatus of fuzzy sets (L. Zade, E. Mamdani, Bellman). In the second period (70–80s) the first practical results in the field of fuzzy control of complex technical systems (steam generator with fuzzy control) appear. At the same time, attention was paid to building expert systems based on fuzzy logic and developing fuzzy controllers. Fuzzy expert systems to support decision-making are widely used in medicine and economics. Finally, in the third period, which lasts from the end of the 80s and continues at present, software packages for building fuzzy expert systems appear, and the areas of application of fuzzy logic are noticeably expanding. It is used in the automotive, aerospace and transportation industries, in the field of household appliances, in the field of finance, analysis and management decision-making, and many others.

The triumphal procession of fuzzy logic around the world began after the proof in the late 80s by Bartholomew Kosco of the famous FAT (Fuzzy Approximation Theorem). In business and finance, fuzzy logic gained recognition after in 1988 the expert system based on fuzzy rules for forecasting financial indicators was the only one to predict a stock market crash. And the number of successful fuzzy applications is currently in the thousands.

Mathematical apparatus

A characteristic of a fuzzy set is the Membership Function. Let MFc (x) denote the degree of belonging to the fuzzy set C, which is a generalization of the concept of the characteristic function of an ordinary set. Then a fuzzy set C is a set of ordered pairs of the form C = {MFc (x) / x}, MFc (x) [0,1]. The value MFc (x) = 0 means the absence of membership in the set, 1 - full membership.

We illustrate this with a simple example. We formalize the inaccurate definition of "hot tea". The temperature scale in degrees Celsius will act as x (the area of ​​reasoning). Obviously, it will vary from 0 to 100 degrees. A fuzzy set for the term "hot tea" may look like this:

C = {0/0; 0/10; 0/20; 0.15 / 30; 0.30 / 40; 0.60 / 50; 0.80 / 60; 0.90 / 70; 1/80; 1/90; 1/100}.

So, tea with a temperature of 60 ° C belongs to the set "Hot" with a degree of membership of 0.80. For one person, tea at a temperature of 60 ° C may turn out to be hot, for another - not too hot. This is where the fuzziness of the task of the corresponding set manifests itself.

For fuzzy sets, as for ordinary ones, the basic logical operations are defined. The most basic ones needed for calculations are intersection and union.

Intersection of two fuzzy sets (fuzzy "AND"): AB: MFAB (x) = min (MFA (x), MFB (x)).
The union of two fuzzy sets (fuzzy "OR"): AB: MFAB (x) = max (MFA (x), MFB (x)).

In the theory of fuzzy sets, a general approach to the execution of intersection, union, and complement operators has been developed, implemented in the so-called triangular norms and conorms. The above implementations of intersection and union operations are the most common cases of t-norm and t-conorm.

To describe fuzzy sets, the concepts of fuzzy and linguistic variables are introduced.

A fuzzy variable is described by the set (N, X, A), where N is the name of the variable, X is the universal set (the domain of reasoning), A is the fuzzy set on X.
The values ​​of a linguistic variable can be fuzzy variables, i.e. the linguistic variable is at a higher level than the fuzzy variable. Each linguistic variable consists of:

• Names
• sets of their values, which is also called the base term-set T. Elements of the basic term-set are the names of fuzzy variables;
• universal set X;
• syntax rule G, according to which new terms are generated using the words of a natural or formal language;
• semantic rule P, which associates each value of a linguistic variable with a fuzzy subset of the set X.

Consider such a fuzzy concept as "Share Price". This is the name of the linguistic variable. We form a basic term-set for it, which will consist of three fuzzy variables: “Low”, “Moderate”, “High” and set the area of ​​reasoning in the form X = [100; 200] (units). The last thing left to do is to build membership functions for each linguistic term from the base term-set T.

There are over a dozen typical curve shapes for specifying membership functions. The most common are: triangular, trapezoidal and Gaussian membership functions.

The triangular membership function is determined by a triple of numbers (a, b, c), and its value at the point x is calculated according to the expression:

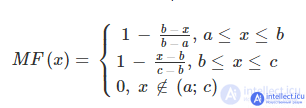
For (ba) = (cb), we have the case of a symmetric triangular membership function, which can be uniquely determined by two parameters from the triple (a, b, c).

Similarly, to specify a trapezoidal membership function, you need four numbers (a, b, c, d):

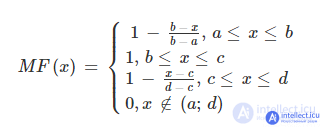
For (ba) = (dc) the trapezoidal membership function takes a symmetrical form.

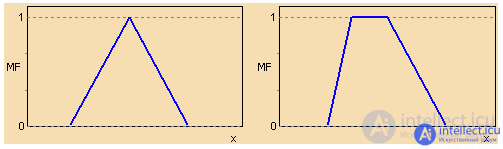
Figure 1. Typical piecewise linear membership functions

The membership function of a Gaussian type is described by the formula

MF (x) = exp [- (x − cσ) 2] MF (x) = exp⁡ [- (x − cσ) 2]

and operates with two parameters. The parameter c denotes the center of the fuzzy set, and the parameter is responsible for the steepness of the function.

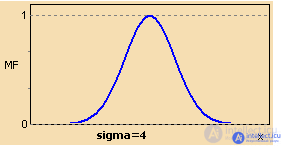
Figure 2. Gaussian membership function

The set of membership functions for each term from the base term set T is usually depicted together on the same graph. Figure 3 shows an example of the linguistic variable "Stock Price" described above, and Figure 4 shows a formalization of the inaccurate concept of "Human Age". So, for a person 48 years old, the degree of belonging to the set "Young" is 0, "Average" - 0.47, "Above average" - 0.20.

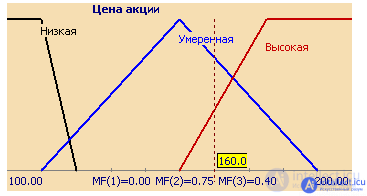
Figure 3. Description of the linguistic variable "Stock Price"

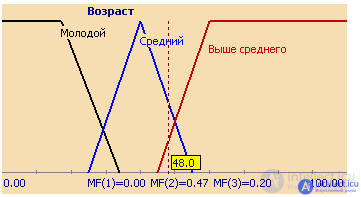
Figure 4. Description of the linguistic variable "Age"

The number of terms in a linguistic variable rarely exceeds 7.

Fuzzy inference

The basis for the operation of fuzzy inference is the rule base containing fuzzy statements in the form of "If" and membership functions for the corresponding linguistic terms. In this case, the following conditions must be met:

1. There is at least one rule for each linguistic term of the output variable.
2. For any term of an input variable, there is at least one rule in which this term is used as a prerequisite (the left part of the rule).

Otherwise, there is an incomplete base of fuzzy rules.

Let the rule base have m rules of the form:
R1: IF x1 is A11 ... And ... xn is A1n, THEN y is B1
...
Ri: IF x1 is Ai1 ... And ... xn is Ain, THEN y is Bi
...
Rm: IF x1 is Ai1 ... And ... xn is Amn, THEN y is Bm,
where xk, k = 1..n are input variables; y is the output variable; Aik are given fuzzy sets with membership functions.

The result of fuzzy inference is a clear value of the variable y * based on the given clear values ​​xk, k = 1..n.

In the general case, the inference mechanism includes four stages: introduction of fuzziness (phaseization), fuzzy inference, composition and reduction, or dephasing (see Figure 5).

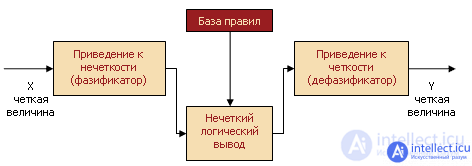
Figure 5. Fuzzy inference system

Fuzzy inference algorithms differ mainly in the type of rules used, logical operations, and a variety of the defazification method. The models of fuzzy inference of Mamdani, Sugeno, Larsen, Tsukamoto are developed.

Let us consider in more detail the fuzzy conclusion on the example of the Mamdani mechanism. This is the most common inference method in fuzzy systems. It uses the minimax composition of fuzzy sets. This mechanism includes the following sequence of actions.

1. Phasing procedure: degrees of truth are determined, i.e. values ​​of membership functions for the left-hand sides of each rule (premises). For a rule base with m rules, we denote the degrees of truth as Aik (xk), i = 1..m, k = 1..n.

2. Fuzzy conclusion. First, clipping levels are determined for the left side of each of the rules:

   

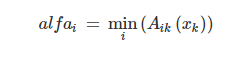
   The following are the "truncated" membership functions:

   

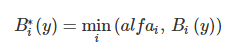
3. The composition, or the union of the obtained truncated functions, for which the maximum composition of fuzzy sets is used:

   

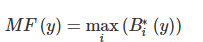
   where MF (y) is the membership function of the resulting fuzzy set.

4. Defazification, or clarity. There are several defazification methods. For example, the middle center method, or the centroid method:

   

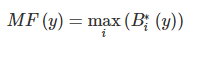
The geometric meaning of this value is the center of gravity for the curve MF (y). Figure 6 graphically shows the Mamdani fuzzy inference process for two input variables and two fuzzy rules R1 and R2.

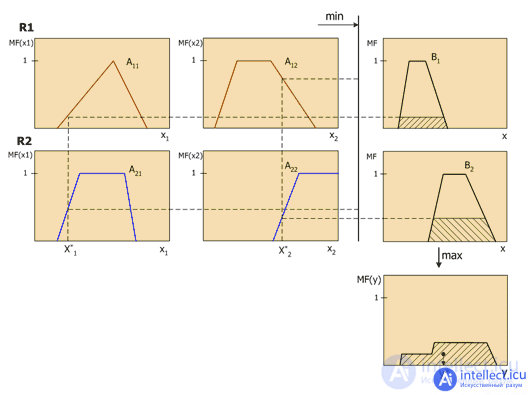
Figure 6. Fuzzy inference diagram for Mamdani

Intelligent paradigm integration

Hybridization of methods of intellectual information processing is the motto under which the 90s passed by Western and American researchers. As a result of combining several technologies of artificial intelligence, a special term appeared - soft computing, which was introduced by L. Zadeh in 1994. Currently, soft computing unites such areas as fuzzy logic, artificial neural networks, probabilistic reasoning, and evolutionary algorithms. They complement each other and are used in various combinations to create hybrid intelligent systems.

The influence of fuzzy logic turned out to be perhaps the most extensive. Just as fuzzy sets expanded the scope of the classical mathematical set theory, fuzzy logic “invaded” practically the majority of Data Mining methods, endowing them with new functionality. The following are the most interesting examples of such associations.

Fuzzy neural networks

Fuzzy-neural networks draw conclusions based on the fuzzy logic apparatus, however, the parameters of membership functions are configured using NS learning algorithms. Therefore, to select the parameters of such networks, we apply the back propagation method of error, which was originally proposed for training a multilayer perceptron. For this, the fuzzy control module is presented in the form of a multilayer network. A fuzzy neural network typically consists of four layers: a phaseification layer of input variables, an aggregation layer of condition activation values, an aggregation layer of fuzzy rules, and an output layer.

Currently, fuzzy NS architectures of the ANFIS and TSK type are most widely used. It is proved that such networks are universal approximators.

Fast learning algorithms and the interpretability of accumulated knowledge - these factors have made fuzzy neural networks one of the most promising and effective soft computing tools today.

Adaptive Fuzzy Systems

Classical fuzzy systems have the disadvantage that in order to formulate the rules and membership functions, it is necessary to attract experts from a particular subject area, which is not always possible to provide. Adaptive fuzzy systems solve this problem. In such systems, the selection of the parameters of the fuzzy system is carried out in the learning process on experimental data. Learning algorithms for adaptive fuzzy systems are relatively time-consuming and complex compared to learning algorithms for neural networks, and, as a rule, consist of two stages: 1. Generation of linguistic rules; 2. Correction of membership functions. The first problem relates to a sorting problem, the second relates to optimization in continuous spaces. In this case, a certain contradiction arises: membership functions are necessary for generating fuzzy rules, and rules are necessary for fuzzy inference. In addition, with the automatic generation of fuzzy rules, it is necessary to ensure their completeness and consistency.

A significant part of the methods for teaching fuzzy systems uses genetic algorithms. In English literature, this corresponds to a special term - Genetic Fuzzy Systems.

A significant contribution to the development of the theory and practice of fuzzy systems with evolutionary adaptation was made by a group of Spanish researchers led by F. Herrera.

Fuzzy queries

Fuzzy queries to databases (fuzzy queries) are a promising area in modern information processing systems. This tool makes it possible to formulate requests in a natural language, for example: "List the low-cost offers for renting housing close to the city center," which is impossible using the standard request mechanism. For this purpose, fuzzy relational algebra and special SQL language extensions for fuzzy queries have been developed. Most of the research in this area belongs to the West European scientists D. Dubois and G. Prade.

Fuzzy Associative Rules

Fuzzy associative rules are a tool for extracting patterns from databases that are formulated as linguistic statements. Special concepts of fuzzy transaction, support and reliability of a fuzzy associative rule are introduced here.

Fuzzy cognitive maps

Fuzzy cognitive maps were proposed by B. Kosco in 1986 and are used to model the causal relationships identified between the concepts of a certain area. Unlike simple cognitive maps, fuzzy cognitive maps are a fuzzy oriented graph whose nodes are fuzzy sets. The directed edges of the graph not only reflect causal relationships between the concepts, but also determine the degree of influence (weight) of the connected concepts. The active use of fuzzy cognitive maps as a means of modeling systems is due to the possibility of a visual representation of the analyzed system and the ease of interpretation of cause-effect relationships between concepts. The main problems are related to the process of constructing a cognitive map, which cannot be formalized. In addition, it is necessary to prove that the constructed cognitive map is adequate to the real simulated system. To solve these problems, algorithms have been developed for automatic construction of cognitive maps based on data sampling.

Fuzzy clustering

Fuzzy clustering methods, in contrast to clear methods (for example, Kohonen neural networks), allow the same object to belong to several clusters at the same time, but with varying degrees. Fuzzy clustering in many situations is more "natural" than clear, for example, for objects located on the border of clusters. The most common are: the c-means fuzzy self-organization algorithm and its generalization in the form of the Gustafson-Kessel algorithm.

The list goes on and on: fuzzy decision trees, fuzzy Petri nets, fuzzy associative memory, fuzzy self-organizing cards, and other hybrid methods.

LITERATURE

• Zade L. The concept of a linguistic variable and its application to making approximate decisions. - M .: Mir, 1976.
• Kruglov V.V., Dli M.I. Intelligent information systems: computer support for fuzzy logic systems and fuzzy inference. - M .: Fizmatlit, 2002.
• Leolenkov A.V. Fuzzy modeling in MATLAB and fuzzyTECH. - SPb., 2003.
• Rutkovskaya D., Pilinsky M., Rutkovsky L. Neural networks, genetic algorithms and fuzzy systems. - M., 2004.
• Masalovich A. Fuzzy logic in business and finance. www.tora-centre.ru/library/fuzzy/fuzzy-.htm
• Kosko B. Fuzzy systems as universal approximators // IEEE Transactions on Computers, vol. 43, No. 11, November 1994. - P. 1329-1333.
• Cordon O., Herrera F., A General study on genetic fuzzy systems // Genetic Algorithms in engineering and computer science, 1995. - P. 33-57.