Lecture
Fuzzy inference can be implemented using different algorithms, since each stage of the inference allows using different calculation methods and parameters. Consider the most popular algorithms.
The rules of the knowledge base of the Mamdani algorithm (Mamdani E.N.) has the form:
(if there is x - "(g)". to 2 is " 2> " 0 ??? "x l is ") THEN to k has d kj with weight w. 9
where l :, is the / -th (/ = 1, 2, ..., n ) is the input linguistic variable, and i} is the term of the / -th variable in the / -th rule (J = 1,2, ... , / and), y k is the k-th output variable (k = 1,2, ..., n ), d ki is the conclusion of the k- th variable in the y-th rule (a rule can contain several subconnections connected by logical operations ), w- is the weight of the th rule, 0 is the logical operation AND or OR.
In the aggregation procedure (calculating the degree of truth of conditions) for each of the rules of the fuzzy inference system for the input vector x * = [**, x * 2 , ..., **] the formula is used
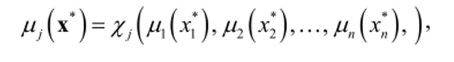
where // Д х) is the degree of truth of the condition of the / -th rule, / r (x *) is the result of fuzzification of the input variable x, -, Zj means the t-norm, if only the logical operation And is used in the / -th rule, and means s-norm, if only logical operation OR is used in the j- th rule. In the Mamdani algorithm, the t-norm is usually realized by the minimum operation, and the s-norm by the maximum operation. If the condition contains different logical operations, then in the absence of brackets, the AND operations (t-norm) are first performed, and then OR (s-norm). The brackets upset the order of operations.
The truth of each subclause (activation procedure) is equal to n. O ') = minjvvyr (x'), ^ (y)} where Wj is the weight of the y-th rule; // Дх) - the degree of truth of the condition of the / -th rule found in the aggregation procedure; ju d (y) is the membership function of the nth output quantity in the ith rule.
Unified resulting membership function / g ,. for each output variable (accumulation procedure) in the Mamdani algorithm is found using the maximum operation on the membership functions of the sub-conditions of the subclauses related to one output variable.
A clear value of the output variable y [ (defuzzification procedure) is usually performed by the method of center of gravity
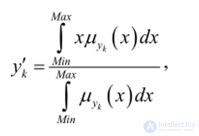
where Min and Max are the left and right points of the interval of the medium of the output variable y k .
A feature of the Sugsno-Takagi algorithm (T. Takagi, M. Sugeno) is the representation of knowledge base rules in the form
(IF "*, there is 1 / " & "x 2 is 2 " 0 ? ?? "x is ") THEN y t = c > (| + with y1 lg, + ... + with j „x„
where Xj is the lth (i = 1, 2, n) input linguistic variable, aij is the germ of the i-th variable in the ith rule (/ = 1,2, ..., m), I am the output variable (k = 1, 2, n ), c j0 , c jb c jn are real numbers, 0 is the logical operation AND or OR.
The conclusions of the rules in the Sugeno-Takagi knowledge base are linear input functions.
The fuzzification procedure does not differ from the fuzzification in the Mamdani algorithm. In the procedure for aggregating subconditions, as a rule, the operation of min conjunction is used. In the procedure for activating conclusions, clear values of the output variables of each y-th rule are calculated as linear
functions of input values of unfuzzified variables * *
y kj = c J0 + Cj ^ + ... + c Jn x „. There is no stage of accumulation of conclusions in this algorithm, since the output variables are clear. Formally, the output sets are single-point sets. Therefore, for defuzzification, the center of gravity method for single-point sets can be used
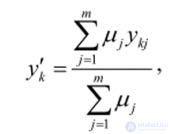
where y [ is the clear value of the output variable y b // ; is the degree of truth of the y-th condition, y kj is the value of the output variable y k calculated by the w-th condition.
Other fuzzy inference algorithms can be found in [5, 7, 12, 24].
Comments
To leave a comment
Computational Intelligence
Terms: Computational Intelligence