ADAPTIVE GENETIC ALGORITHM FOR “SOFT” EVOLUTION CALCULATIONS

Introduction

In modern engineering and other sectors of the economy, the so-called technological processes with loosely coupled subsystems (TPSP) and technological equipment with loosely coupled parameters (TOSP) are widely used. An example of TPPS is the casting process, in which the liquid metal filling temperatures of individual parts of the casting are interconnected by the total temperature of the metal in the bucket stream, but this connection is not “hard” - in different parts (subsystems) the temperatures can differ by some limited by the process conditions, value. Objects of the same class include multi-thread thread grinding [1], multi-strand continuous casting [2] and many others.

Formulation of the problem.

Problems in the design and management of such processes arise when it is necessary to calculate the values ​​of some argument parameters that deliver the maximum (minimum) of the specified objective functions, i.e. in solving optimization problems. The fact is that, due to the complexity of the objective functions in TPPS and TOSP, analytical optimization methods are not applicable to them, and numerical methods require poiter variation of the argument values, which is very difficult in conditions of mutual communication, in general, of functionally distant characteristics related to different subsystems. This is evidenced by the site https://intellect.icu.

Analysis of recent achievements and publications.

Recently, the evolutionary method for optimizing multi-extreme systems, called the genetic algorithm (GA) [3 ... 5], has become widespread. As you know, the basic calculations in classical GA are carried out at the level of the so-called “chromosomes” - symbolic models that carry information about the arguments of the objective function. If the subsystems in the optimized system are independent - the objective functions in them are different, and the sets of argument values ​​of these functions do not intersect, then such subsystems are not connected from the point of view of the problem under consideration, and its formulation splits into several independent classical optimization problems. If the sets of values ​​of the arguments of the objective functions in the subsystems overlap at least partially, the task becomes “tough”, because varying the related arguments in one subsystem, we are involuntarily forced to equally vary them in another. It was proposed to solve such problems with the help of a complex GA, generating complex star-shaped chromosomes that take into account hard bonds [6, 7]. Recently, papers have appeared that introduce a new kind of chromosomes — with a “soft” connection of arguments, in which the related arguments can still differ for the two subsystems, but no more than by a certain value Smax [8, 9]. Such a restriction contradicts the main property of the GA: the free variation of the arguments when solving the optimization problem. Indeed, at each epoch of the evolution of GA, descendant chromosomes may appear that do not satisfy the specified limitation, which leads to an emergency stop of the algorithm program. The appearance of such descendants in relatively large quantities (which is observed in practice) makes even a complex GA unsuitable for optimization calculations. This requires the creation of an alternative GA, containing in its composition a new method of crossing chromosomes, adapting to the constantly emerging problems of limitations of “soft” connectivity

The purpose of the work is to increase the efficiency of design and control due to deeper optimization of parameters of objects with loosely coupled subsystems by developing an adaptive genetic algorithm for “soft” evolutionary calculations.

Main material.

The fundamental property of GA is that in the process of optimization the arguments can take any values ​​from the area bounded by their minimum and maximum acceptable values, for example, for the objective function N arguments y (x); 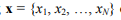the region of existence of chromosomes (region of optimization) is limited by the expressions:

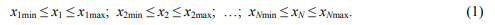
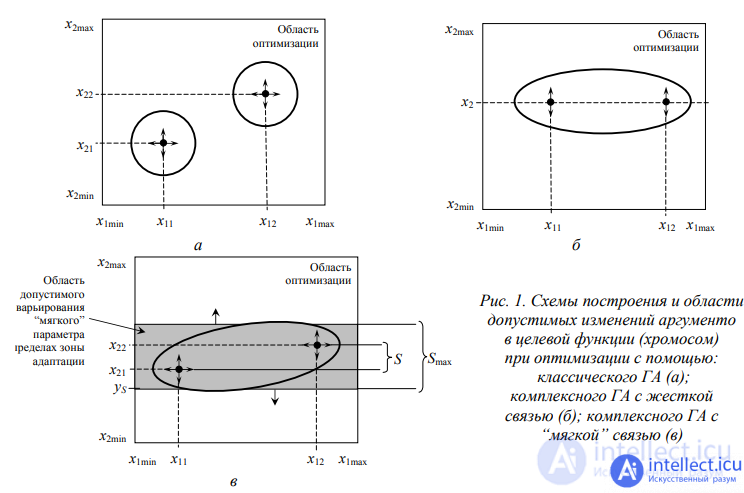
In fig. 1, and as an example, two two-parameter unconnected chromosomes of two subsystems of one system are shown, as well as a common (coinciding in all arguments) range of acceptable values ​​for their four arguments 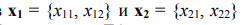in the process of optimizing objective functions 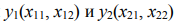using GA. Unlike the two classical ones, with a “hard” - mathematically rigorous - connection, one complex chromosome carries information about three arguments: x11, x12 and x2, since they have a common argument x2 (Fig. 1, b). At the same time, it preserves the main property of GA: free variation within the limits of general restrictions (1). With a “soft” connection, new ones are added to the constraints (1):

for each group of related arguments, consisting, in the general case, of 2, 3, ..., N elements. In the corresponding “soft” complex two-parameter chromosome, as in the first case, four variables are stored again: х11, х12, х21, х22, S (Fig. 1, c), however, the memory of such a GA contains the Smax value for each “soft” connection .

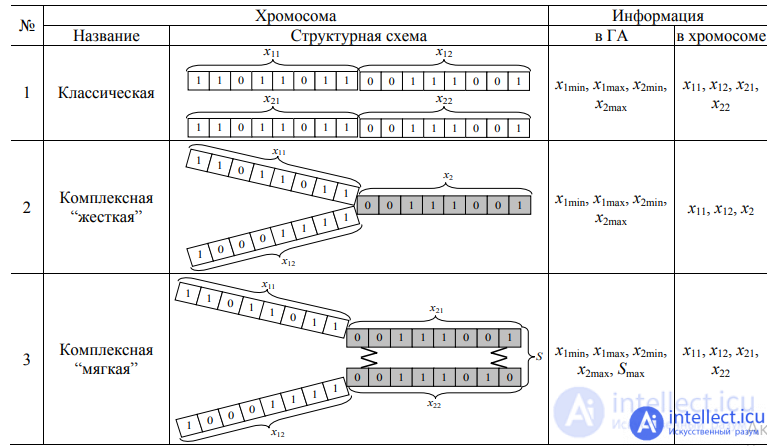
The structural diagram of the classical, as well as complex “hard” and “soft” chromosomes for the case of two arguments, as well as the information contained in them and in the memory of the corresponding GA, are given in the table.

Schemes of symbolic models (chromosomes) and the information contained in them for two two-parameter subprocesses

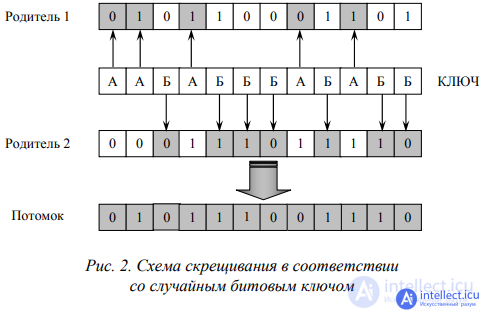
Adaptation of the algorithm for optimizing an object with loosely coupled subsystems was carried out at the stage of crossing the GA. In contrast to the classical GA, in which point, two-point, and multi-point crosses are most often used, uniform cross-section, otherwise called monolithic or single-stage, was used in complex GA with “soft” bonds.

This crossover is performed in accordance with a randomly selected bit key that indicates which genes should be inherited from the first and which from the second parent. Suppose that the standard AABABBBABABABB is chosen, in which A means the adoption of a gene at the appropriate position from the first parent, and B from the second. Thus, the first descendant is formed (Fig. 2). For the second child, the key is read inversely: B means accepting the gene at the appropriate position from the first parent, and A from the second

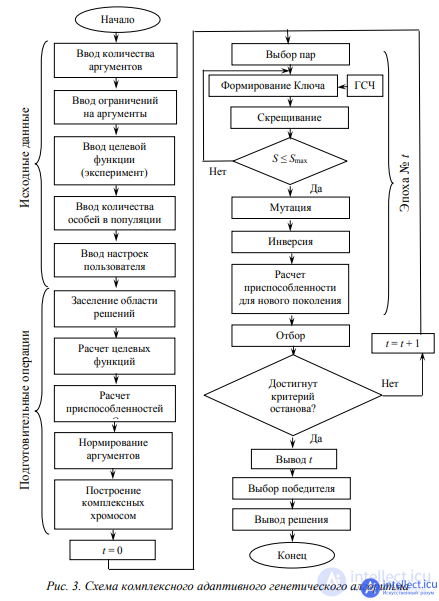
. All descendants obtained in this way undergo mutations and inversions and then pass the verification of the fulfillment of condition (2), and if it is not fulfilled, the same parents cross again, but with a different, randomly selected key. The experiment shows that a “mild” crossover operation combined with “hard” mutation and inversion operations is sufficient to produce offspring at an acceptable time, subject to restrictions on connectivity. If, however, the problem cannot be solved, the adaptive approach can also be extended to the mutation with inversion, which will provide the user with much more options for choosing chromosome variants for posterity. The scheme of the complex adaptive genetic algorithm is shown in Fig. 3, it contains crossing adaptation blocks that “monitor” the fulfillment of the above restrictions on the optimization process.

The work of the adaptive genetic algorithm for “soft” evolutionary calculations was tested in the framework of CAD of the multi-jet continuous casting process of copper. It has been established in production that the main indicator of the quality of the ingots obtained in this case is the relative elongation of the metal δ in tensile tests, and the main technological characteristics affecting δ are the average extrusion rate V of the ingot and the temperature of the cooling water at the inlet to the mold T.

Due to the different arrangement of the molds relative to the point of entry of the liquid metal into the transfer furnace to obtain continuous castings of the best quality, the parameters of the draw and cooling subprocesses for each of them should differ, while remaining within the limits of connectivity. Calculations were performed for two parallel-working crystallizers cooled from a single water source (T connection), from which the ingots were extracted with the same type of drawing devices (V connection). The process conditions allow you to vary the parameters V and T within 3.2 ≤ V ≤ 3.6 m / min and 20 ≤ T ≤ 32 ° C.

Due to the intermittent drawing mode of the ingots and the resulting low-frequency oscillations, the functions δ1 (V1, T1) and δ2 (V2, T2) (indices 1 and 2 belong to different crystallizers) are multi-extremal. Under these conditions, a complex adaptive GA was used for calculations, which allowed us to calculate the optimal process parameters: V1 = 3.37 m / min; T1 = 22 ° C; V2 = 3.54 m / min; T2 = 29 ° C.

Conclusions The proposed method for optimizing the parameters of objects with loosely coupled subsystems, consisting in the application of the developed adaptive genetic algorithm for “soft” evolutionary calculations, made it possible to increase the optimization depth and obtain a positive technical effect in computer experiments.

Literature

1. Thin-footed, V.M. Multipurpose optimization by the method of complex genetic algorithm / V.M. Thinfoot, A.A. Perperi, D.A. Monova // Advanced technology in machine blowing: ЗБ. sciences. pr. - VIP. 6. - Kharkiv, NTU “KhPI”, 2011. - S. 276 - 281.

2. Prokopovich, O.I. Wire rod surface temperature as an indirect parameter of quality management / O.I. Prokopovich, I.V. Prokopovich, V.D. Gogunsky // Tr. Odessa Polytechnic un-that. - Odessa, 2003. - Vol. 2 (20). - S. 128 - 130.

3. Rothstein, A.P. Intelligent identification technologies: fuzzy sets, genetic algorithms, neural networks. - Vinnitsa: Universum-Vinnitsa, 1999 .-- 320 p.

4. Skurikhin, A.N. Genetic Algorithms // Artificial Intelligence News. - 1995. - No. 4. - S. 6 - 46.

5. Zmitrovich, A.I. Intelligent information systems. - Minsk: Tetrasystems, 1997 .-- 368 p.

6. Monova, D.A. Complex genetic algorithm / D.A. Monova, A.A. Perperi, P.S. Shvets // Ave. Odessa polytechn. un-that. - Odessa, 2011. - VIP. 1 (35). - S. 176 - 180

. 7. Perperi, A.O. Modernization of the mathematical method of the genetic algorithm for optimizing mutual technological processes / A.O. Perperі, L.A. Odukalets, D.A. Monova, P.S. Shvets // Model and information technology: Зб. sciences. pr. In-tu problems modeling in energy im. G.Є. Pukhova NAS of Ukraine. - 2011. - VIP. 60.- S. 90 - 94.

8. Stanovsky, A.L. Evolutionary optimization of loosely coupled technical systems in CAD / A.L. Stanovsky, P.S. Shvets, D.A. Zheldubovsky // Ave. Odessa polytechn. un-that. - 2011. - VIP. 2 (36). - S. 234 - 238.

9. Stanovsky, A.L. Optimization of loosely coupled systems in computer aided design and control / A.L. Stanovsky, P.S. Shvets, I.N. Generous. // Advanced technology in machine learning: zb. sciences. pr. - VIP. 6. - Kharkiv, NTU “KhPI", 2011. - S. 129 - 134.