Collaborative filtering , collaborative filtering ( collaborative filtering ) is one of the methods for constructing forecasts (recommendations) in recommender systems [] , using known preferences (estimates) of a group of users to predict unknown preferences of another user. [1] Its basic assumption is as follows: those who have equally evaluated any items in the past tend to give similar marks to other items in the future. [1] For example, using collaborative filtering, a music application can predict which music a user will like [] , having an incomplete list of his preferences (likes and dislikes). [2] Forecasts are made individually for each user, although the information used is collected from many participants. Thus, collaborative filtering differs from a simpler approach, which gives an average estimate for each object of interest, for example, based on the number of votes cast for it. Research in this area is actively conducted in our time, which is also caused by the presence of unsolved problems in collaborative filtering. [⇨]

Content

• 1 Description
• 2 Types of collaborative filtering
  • 2.1 Based on neighborhood
  • 2.2 Based on model
  • 2.3 Hybrid
• 3 problems
  • 3.1 Data Sparse
  • 3.2 Scalability
  • 3.3 Cold start problem
  • 3.4 Synonymy
  • 3.5 Fraud
  • 3.6 Diversity
  • 3.7 White Ravens
• 4 Application in social networks
• 5 See also
• 6 Notes
• 7 Literature

Description

In the age of information explosion, such methods of creating personalized recommendations, such as collaborative filtering, are very useful, since the number of objects even in one category (such as movies, music, books, news, websites) has become so large that an individual cannot see all of them to choose the right ones.

Collaborative filtering systems usually use a two-step scheme [1] :

1. Find those who share the judgments of the "active" (predictable) user.
2. Use the estimates of like-minded people found in the first step to calculate the forecast.

The algorithm described above is built relative to the users of the system.

There is also an alternative algorithm invented by Amazon [3] , constructed with respect to the items (products) in the system. This algorithm includes the following steps:

1. We build a matrix that determines the relationship between pairs of objects, to find similar objects.
2. Using the constructed matrix and information about the user, we build predictions of his estimates.

For an example, see the Slope One family of algorithms.

There is also another form of collaborative filtering, which is based on the hidden observation of ordinary user behavior (as opposed to the explicit one that collects user ratings). In these systems, you observe how a given user acted, and how - others (what music they listened to, what videos they watched, what compositions they purchased), and use the data to predict the user's behavior in the future, or predict how the user would like to act with a certain opportunity. These predictions should be made according to business logic, as for example, it is useless to offer someone to buy a music file that they already have.

Types of collaborative filtering

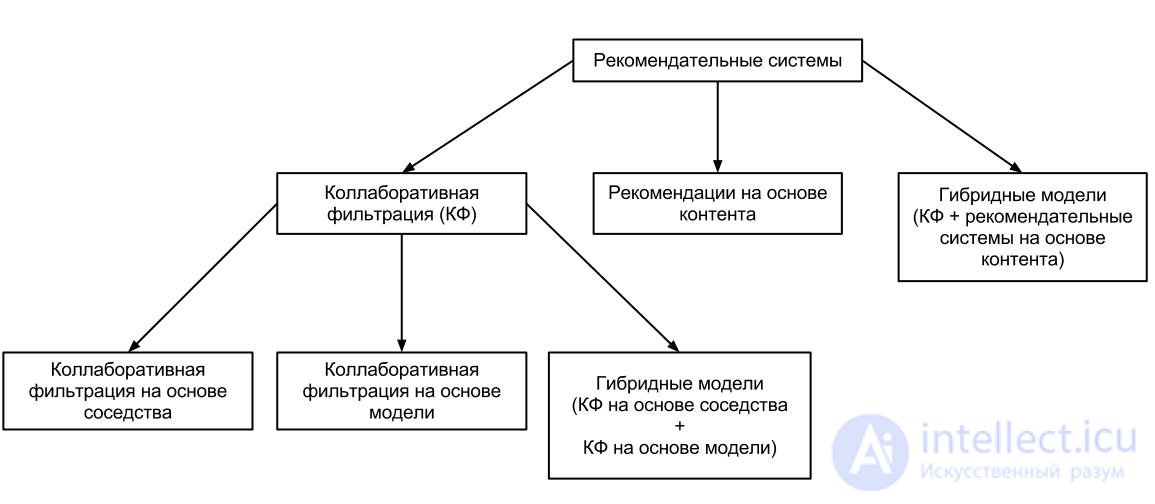
Types of collaborative filtering

There are 2 main methods used to create recommender systems - collaborative filtering and content-based recommendations. Also in practice, a hybrid method of building recommendations is used, which includes a mixture of the above methods. Collaborative filtering, in turn, is also divided into 3 main approaches (type) [4] :

Neighborhood based

This approach is historically the first in collaborative filtering and is used in many recommender systems. In this approach, for the active user, a subgroup of users similar to him is selected. The combination of weights and subgroup ratings is used to predict active user ratings [5] . The following basic steps can be distinguished in this approach:

1. Assign weight to each user, taking into account the similarity of his ratings and the active user.
2. Choose several users who have the maximum weight, that is, they are as close as possible to the active user. This group of users is called neighbors [6] .
3. Calculate the prediction of the estimates of the active user for items not rated by him, taking into account the weights and estimates of the neighbors.

Based on model

This approach provides recommendations by measuring the parameters of statistical models for user ratings constructed using methods such as Bayesian network method, clustering, latent semantic model, such as singular decomposition, probabilistic latent semantic analysis, Dirichlet hidden distribution and Markov decision-making process models. [5] Models are developed using data mining, machine learning algorithms to find patterns based on training data. The number of parameters in the model can be reduced depending on the type using the principal component method.

This approach is more complex and provides more accurate predictions, as it helps to reveal the latent factors that explain the observed estimates. [7]

This approach has several advantages. It handles sparse matrices better than the neighborhood-based approach, which in turn helps with the scalability of large data sets.

The disadvantages of this approach are the “expensive” model creation [8] . A trade-off is needed between accuracy and model size, since it is possible to lose useful information due to model reduction.

Hybrid

This approach combines a neighborhood-based and model-based approach. The hybrid approach is the most common in developing recommender systems for commercial sites, as it helps overcome the limitations of the original original approach (based on the neighborhood) and improve the quality of predictions. This approach also overcomes the problem of data sparseness [⇨] and loss of information. However, this approach is complex and expensive to implement and use. [9]

Problems

Sparseness of data

As a rule, most commercial recommender systems are based on a large amount of data (goods), while most users do not rate products. In the results of this, the “subject-user” matrix is ​​very large and sparse, which presents problems when calculating recommendations. This problem is especially acute for new, just appeared systems. [4] Also, the sparseness of the data intensifies the cold start problem.

Scalability

With the increase in the number of users in the system, there is a problem of scalability. For example, having 10 million buyers 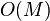and a million items 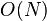, collaborative filtering algorithm with complexity equal to 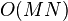already too complicated for calculations. Also, many systems must instantly respond to online requests from all users, regardless of the history of their purchases and ratings, which requires even greater scalability.

Cold start problem

New items or users present a big problem for recommender systems. The content analysis approach helps in part because it relies not on evaluations, but on attributes, which helps to include new items in user recommendations. However, the problem of providing a recommendation for a new user is more difficult to solve. [four]

Synonymy

Synonymy refers to the tendency of similar and identical objects to have different names. Most recommender systems are not able to detect these hidden connections and therefore treat these items as different. For example, “films for children” and “children's film” refer to the same genre, but the system perceives them as different. [five]

Fraud

In recommender systems where everyone can rate, people can give positive marks to their subjects and bad ones to their competitors. Also, recommender systems began to strongly influence sales and profits, since they were widely used in commercial sites. This leads to the fact that unscrupulous suppliers try to fraudulently raise the rating of their products and lower the rating of their competitors. [four]

Diversity

Collaborative filtering is initially recognized to increase diversity, to allow users to discover new products from countless. However, some algorithms, in particular, those based on sales and ratings, create very difficult conditions for promoting new and little-known products, since they are replaced by popular products that have been on the market for a long time. This in turn only increases the effect of “the rich become even richer” and leads to less variety. [ten]

White crows

The "white crows" are users, whose opinion does not always coincide with most of the rest. Because of their unique taste, it is impossible for them to recommend anything. However, such people have problems with receiving recommendations in real life, so the search for a solution to this problem is currently not conducted. [five]

Application in social networks

Collaborative filtering is widely used in commercial services and social networks. The first use case is to create a recommendation for interesting and popular information based on the community “votes”. Services such as Reddit, Digg or DiCASTA are typical examples of systems using collaborative filtering algorithms.

Another area of ​​use is to create personalized recommendations for the user, based on his previous activity and data on the preferences of other users who are similar to him. This method of implementation can be found on sites such as YouTube, Last.fm and Amazon [3] , as well as in such social services as Gvidi and Foursquare.

Collaborative filtering

In today's world, one often encounters the problem of recommending goods or services to users of an information system. In the old days, for the formation of recommendations, a summary of the most popular products was treated: this can be observed even now by opening Google Play. But over time, such recommendations began to be supplanted by targeted (targeted) offers: users are recommended not just popular products, but those products that will surely appeal to them. Not so long ago, Netflix held a contest with a prize fund of $ 1 million, the task of which was to improve the algorithm for recommending films (more). How do these algorithms work?

This article discusses the algorithm for collaborative filtering by user similarity, determined using a cosine measure, and its implementation in python.

Input data

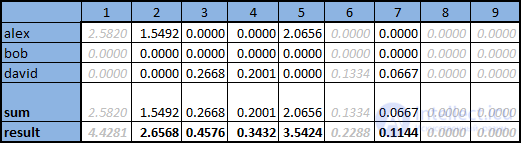
Suppose we have a matrix of user ratings for products, for simplicity, the products are assigned numbers 1-9:


You can set it using a csv-file, in which the first column is the user name, the second is the product identifier, and the third is the user rating. Thus, we need a csv file with the following contents:

alex,1,5.0 alex,2,3.0 alex,5,4.0 ivan,1,4.0 ivan,6,1.0 ivan,8,2.0 ivan,9,3.0 bob,2,5.0 bob,3,5.0 david,3,4.0 david,4,3.0 david,6,2.0 david,7,1.0 

To begin with, we will develop a function that will read the above csv file. For the storage of recommendations, we will use the standard for python data structure dict: each user is assigned a reference book of his ratings of the type “product”: “rating”. The result is the following code:

 import csv def ReadFile (filename = ""): f = open (filename) r = csv.reader (f) mentions = dict() for line in r: user = line[0] product = line[1] rate = float(line[2]) if not user in mentions: mentions[user] = dict() mentions[user][product] = rate f.close() return mentions 

Measure of similarity

It is intuitively clear that in order to recommend the user # 1 of a product, you need to choose from products that some users like 2-3-4-etc., Who are most similar in their estimates to user # 1. How to get the numerical expression of this "similarity" of users? Suppose we have M products. Estimates given by a single user represent a vector in the M-dimensional product space, and we can compare vectors. Among the possible measures are the following:

1. Cosine measure
2. Pearson Correlation Coefficient
3. Euclidean distance
4. Tanimoto coefficient
5. Manhattan distance, etc.

I will discuss the various measures and aspects of their application in more detail in a separate article. For now, suffice it to say that in recommender systems the cosine measure and the Tanimoto correlation coefficient are most often used. Let us consider in more detail the cosine measure, which we are going to implement. The cosine measure for two vectors is the cosine of the angle between them. From the school mathematics course, we remember that the cosine of the angle between two vectors is their scalar product divided by the length of each of the two vectors:

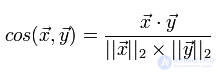
We implement the calculation of this measure, not forgetting that we have a lot of user ratings presented in the form of dict "product": "assessment"

 def distCosine (vecA, vecB): def dotProduct (vecA, vecB): d = 0.0 for dim in vecA: if dim in vecB: d += vecA[dim]*vecB[dim] return d return dotProduct (vecA,vecB) / math.sqrt(dotProduct(vecA,vecA)) / math.sqrt(dotProduct(vecB,vecB)) 

The implementation used the fact that the scalar product of the vector itself gives itself the square of the length of the vector - this is not the best solution in terms of performance, but in our example, the speed of work is not critical.

Algorithm of collaborative filtering

So, we have a user preferences matrix and we can determine how two users resemble each other. Now it remains to implement the algorithm of collaborative filtering, which consists of the following:

1. Select L users whose tastes are most similar to the tastes in question. To do this, for each of the users, you need to calculate the selected measure (in our case, the cosine) with respect to the user in question, and select L the largest. For Ivan, from the table above, we get the following values:
   
2. For each user, his scores will be multiplied by the calculated value of the measure, so the scores of more “similar” users will have a stronger effect on the final position of the product, which can be seen in the table in the illustration below
3. For each of the products, calculate the sum of calibrated ratings of L closest users, divide the resulting amount into the sum of measures L of selected users. The sum is shown in the illustration in the “sum” line, the final value in the “result” line
   
   The columns of products that have already been evaluated by the user in question are marked in gray and it does not make sense to re-offer them to them.

As a formula, this algorithm can be represented as

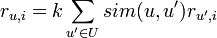
where sim is the chosen measure of similarity between two users, U is the set of users, r is the mark, k is the normalization factor:


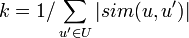
Now you just have to write the appropriate code.

 import math def makeRecommendation (userID, userRates, nBestUsers, nBestProducts): matches = [(u, distCosine(userRates[userID], userRates[u])) for u in userRates if u <> userID] bestMatches = sorted(matches, key=lambda(x,y):(y,x), reverse=True)[:nBestUsers] print "Most correlated with '%s' users:" % userID for line in bestMatches: print " UserID: %6s Coeff: %6.4f" % (line[0], line[1]) sim = dict() sim_all = sum([x[1] for x in bestMatches]) bestMatches = dict([x for x in bestMatches if x[1] > 0.0]) for relatedUser in bestMatches: for product in userRates[relatedUser]: if not product in userRates[userID]: if not product in sim: sim[product] = 0.0 sim[product] += userRates[relatedUser][product] * bestMatches[relatedUser] for product in sim: sim[product] /= sim_all bestProducts = sorted(sim.iteritems(), key=lambda(x,y):(y,x), reverse=True)[:nBestProducts] print "Most correlated products:" for prodInfo in bestProducts: print " ProductID: %6s CorrelationCoeff: %6.4f" % (prodInfo[0], prodInfo[1]) return [(x[0], x[1]) for x in bestProducts] 

To check its performance, you can run the following command:

 rec = makeRecommendation ('ivan', ReadFile(), 5, 5) 

That will lead to the following result:

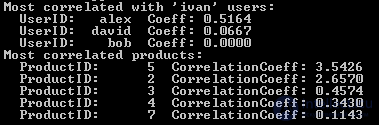
Conclusion

We looked at an example and implemented one of the simplest options for collaborative filtering using a cosine measure of similarity. It is important to understand that there are other approaches to collaborative filtering, other formulas for calculating product ratings, other measures of similarity (article, section "See also"). Further development of this idea can be carried out in the following directions:

1. Optimization of used data structures . When storing data in python in the form of dict, every time a call is made to a specific value, a hash calculation is performed and the situation gets worse the longer the line of names. In practical tasks, sparse matrices can be used to store data, and instead of textual user names and product names, use numeric identifiers (number all users and all products)
2. Performance Optimization . Obviously, to calculate the recommendation for each user request is extremely expensive. There are several ways to work around this issue:
   • Clustering users and calculating the similarity measure only between users belonging to the same cluster
   • Calculation of product-product similarity coefficients. To do this, you need to transpose the use-product matrix (you will get a product-user matrix), after which for each product you can calculate the set of the most similar products using the same cosine measure and remembering the k nearest ones. This is quite a laborious process, so you can produce it once in M hours / days. But now we have a list of products that are similar to this one, and multiplying the user's rating by the value of the measure of product similarity, we get the recommendation for O (N * k) , where N is the number of user ratings
3. Selection of measures of similarity . The cosine measure is one of the frequently used, but the choice of measure should be made only according to the results of the analysis of the system data.
4. Modification of the filtering algorithm . Perhaps a different filtering algorithm will give more accurate recommendations in a particular system. Again, the comparison of different algorithms can be made only when applied to a specific system.