Lecture
View range 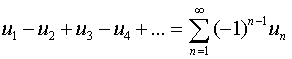 where u n > 0 is called alternating. If a series converges
where u n > 0 is called alternating. If a series converges 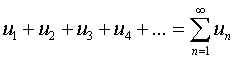 it is said that the alternating series converges absolutely.
it is said that the alternating series converges absolutely.
If the alternating row 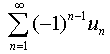 does not absolutely converge, the Leibnitz sign solves the question of its convergence: if
does not absolutely converge, the Leibnitz sign solves the question of its convergence: if 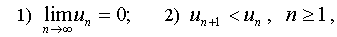 then the alternating series converges, with the sum S of the series being positive and less than u 1 , i.e. 0 < s < u 1 .
then the alternating series converges, with the sum S of the series being positive and less than u 1 , i.e. 0 < s < u 1 .
If the alternating row 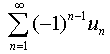 converges, but does not converge absolutely, then they say that the series converges conditionally.
converges, but does not converge absolutely, then they say that the series converges conditionally.
Comments
To leave a comment
Ranks
Terms: Ranks