Examples of solving problems for the section series

Example N 1

Investigate a series on convergence .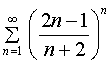

Decision.

Find

Since 2> 1, then, on the basis of Cauchy, the series diverges.

Answer: the series diverges.

Example N 2

Investigate on the convergence series .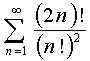

Decision.

Since factorials are present in U n , we use the dalamber sign.

Consequently, on the basis of d'Alembert, the series diverges.

Answer: the series diverges.

Example N 3

Investigate on the convergence series .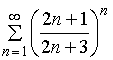

Decision.

The Cauchy symptom does not work in this case, since 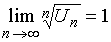. Here we apply the necessary sign of the convergence of series.

Consequently, on the basis of the required characteristic, the series diverges.

Answer: the series diverges.

Example N 4

Investigate on the convergence series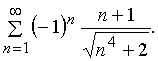

Decision.

Let's make a series of modules of members of our series:

we obtain a sign positive series.

Let's apply the limit sign of comparison. Let's make a row equivalent to a row (*):

series are equivalent. Because 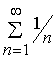- diverges, the series (*) also diverges. Consequently, the original series does not converge absolutely.

We investigate conditional convergence on the basis of Leibniz:

therefore, our series converges conditionally.

Answer: the series converges conditionally.

Example N 5

Find the interval of convergence of the series .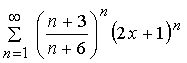

Decision.

Completing the replacement 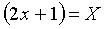get a row 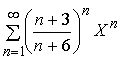. Find the radius of convergence:

,

Consequently, 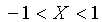By performing a reverse replacement, we get 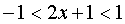. Solve the inequality: , .

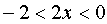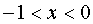Check the convergence of the series on the boundaries of the interval of convergence:

Consequently, the series converges absolutely when 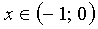in all other points it diverges.

Answer: the series converges absolutely when in all other points it diverges.

Example N 6

Calculate the integral 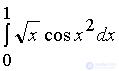accurate to 0.001.

Decision.

Using Maclaurin's series of functions :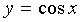

Express the function 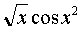via functional range:

Since the region of convergence of this series is the interval 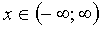and spacing 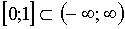, then integrating the obtained series by term, we find:

Received alternating series, therefore, the error in the calculation of the amount does not exceed the modulus of the first rejected member of the series. Find a member of the series, the value of which is less than 0.001:

Therefore, to achieve the required accuracy, it is necessary to drop the member of the series 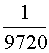and all the following:

Answer:

See also

• 5.1.1. Row definition