You get a bonus - 1 coin for daily activity. Now you have 1 coin

5.2. Numerical series 5.2.1. Signs of comparing rows with positive members

Lecture



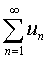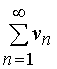Let two rows with positive members be given: 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members and 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members .

If, starting with some natural number N for all n > N, between the corresponding members of the two series, the inequality u n ≥ v n is established , and the series 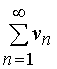5.2. Numerical series 5.2.1. Signs of comparing rows with positive members then the series 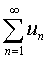5.2. Numerical series 5.2.1. Signs of comparing rows with positive members also diverges.

If, starting with some natural number N, for all n > N, between the corresponding members of the two series, the inequality u n ≤ v n is established , and the series 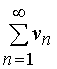5.2. Numerical series 5.2.1. Signs of comparing rows with positive members then the series 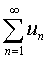5.2. Numerical series 5.2.1. Signs of comparing rows with positive members also converges.

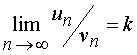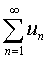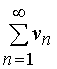If there is a final limit 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members non-zero then both rows 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members and 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members simultaneously converge and diverge at the same time. Such series are called equivalent .

Consider two rows used when comparing rows.

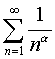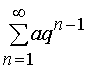  1. Generalized harmonic series: 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members .
    When α > 1, the series converges, with α ≤ 1, the series diverges.
  2. A series of geometric progression: 5.2. Numerical series 5.2.1. Signs of comparing rows with positive members .
    When ‌ q ‌ < 1, the series converges, and when ‌ q ‌ ≥ 1, the series diverges.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Ranks

Terms: Ranks