Shor Algorithm

Shor's algorithm is a quantum factorization algorithm (decomposition of a number into simple factors), which allows decomposing a number 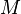duri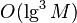ng using 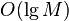logical qubits.

The Shore Algorithm was developed by Peter Shore in 1994. Seven years later, in 2001, its performance was demonstrated by a team of IBM specialists. The number 15 was decomposed into factors 3 and 5 using a quantum computer with 7 qubits.

Peter Shore - the author of the algorithm

About the algorithm

The significance of the algorithm lies in the fact that with its help (using a quantum computer with several hundred logical qubits) it becomes possible to break into public-key cryptographic systems. For example, RSA uses the public key 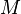, which is the product of two large primes. One way to crack the RSA cipher is to find multipliers. 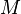. When large enough 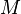it is almost impossible to do using well-known classical algorithms. The best known classical factorization algorithms take time to order. 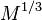. Shor's algorithm, using the capabilities of quantum computers, is capable of factoring a number not just in polynomial time, but in a time that is not much faster than the multiplication time of whole numbers (that is, almost as fast as encryption itself). Thus, the implementation of a scalable quantum computer would put an end to most modern cryptographic protection. (This is not only about the RSA scheme, which is directly based on the complexity of factorization, but also about other similar schemes that a quantum computer can crack in the same way).

Shor's algorithm is probabilistic. The first source of randomness is built into the classical probabilistic reduction of factorization to the determination of the period of a certain function. The second source arises from the necessity of observing quantum memory, which also gives random results ^[1] .

The principle of the algorithm Shor

The basis of the Shor Algorithm: the ability of information units of quantum computers - qubits - to take several values ​​simultaneously and be in a state of "entanglement". Therefore, it allows computations in terms of saving qubits. The principle of operation of Shor’s algorithm can be divided into 2 parts: the first is the classical reduction of the factorization to the determination of the period of a certain function, the second is the quantum determination of the period of this function. Let be:

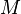- a number that is not a root of an odd number that we want to factor into

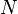- the size of the memory register that is used (not counting the landfill)

The bit size of this memory 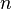about 2 times the size .

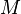More precisely

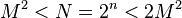
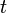- random parameter, such that 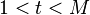and 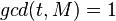, 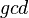- the greatest common divisor.

Note that 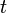, , 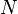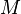- fixed. The Shore algorithm uses the standard method of reducing the decomposition problem to the period search problem. functions for a randomly chosen number 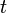^[2] .

Classic algorithm

Minimum such that 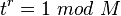- this is order 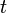modulo .

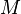Order is the period of the function 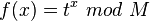where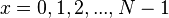

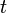If you can efficiently calculate as a function then you can find your own divider 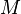for the time limited by the polynomial from 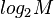with probability 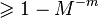for any fixed .

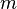Suppose for a given 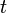period satisfies

.

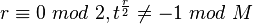Then

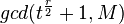- own divider 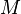. Function computable in polynomial time.

The likelihood of this condition 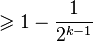where 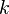- the number of different odd prime divisors 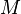, Consequently, 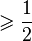in this case. Therefore good value 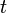with probability 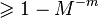there is for 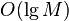attempts. The longest calculation in one attempt is the calculation 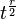^{[3] [4]} .

Quantum algorithm

To implement the quantum part of the algorithm, the computational scheme is 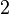quantum register 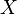and 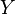. Initially, each of them consists of a set of qubits in the zero boolean state. .

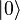Register 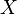used to place arguments 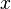functions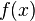

Register 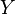(auxiliary) is used to allocate function values. 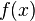with a period to be calculated.

Quantum computing consists of 4 steps ^[5] :

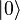• First step. In the first step, using the Walsh-Hadamard operation, the initial state register 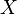translated into an equiprobable superposition of all Boolean states 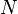. Second register 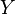remains able 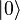. The result is the following state for the system of two registers: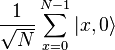

  

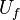• The second step. Let be - unitary transformation that translates 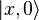at 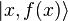. In the second step, a unitary transformation is applied to the system of two registers. It turns out the following system state:

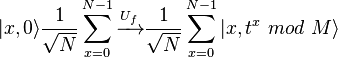, that is, a certain connection is formed between the states of both registers.

• The third step. The quantum Fourier transform is a unitary state transform of the quantum register described by - dimensional vector of the species state 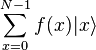to another state :

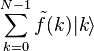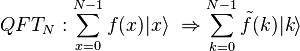where the amplitude of the Fourier transform 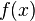has the appearance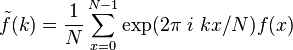

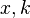In two dimensional -plane Fourier transform corresponds to the rotation of the coordinate axes on 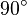which translates the scale 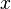to scale 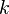. In the third step, the Fourier transform is performed above the state of the first register, and it turns out

.

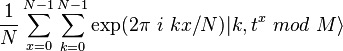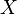• Fourth step. The fourth step is the measurement of the first register relative to the orthogonal projection of the form:

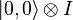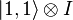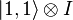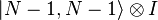, , , ..., where 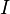- the identical operator on the Hilbert space of the second register .

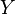The result is 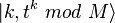with probability

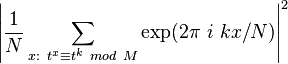^[6]

The rest of the run runs a classic computer:

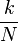• The best approximation (below) to with denominator :

  

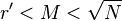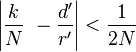
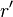• We try in the role :
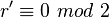  • If a then you should calculate .
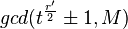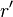  • If a odd or if 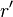even but own divider not detected then repeat run 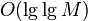times with the same 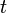. In case of failure to change 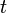and start a new run of the algorithm ^{[3] [4]} .

To some extent, determining the period of a function using the Fourier transform is similar to measuring the lattice constants of a crystal by X-ray or neutron diffraction. To determine the period no need to calculate all values 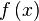. In this sense, the task is similar to the task of Deutsch, in which it is important to know not all the values ​​of a function, but only some of its properties ^[6] .

Finding the period of the function in the algorithm

Let be 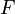- function with an unknown period .

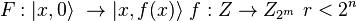
To determine the period two registers with dimensions are require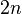d and 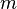qubits, which in their original state must be in

At the first stage, one-sided superposition of all basic vectors of the first register is performed using the operator 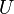of the following type:

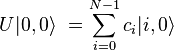where 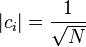and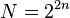

Hadamard pseudo-transform is used here. 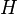. Applying 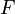to the current state is obtained:

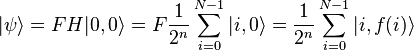
Measurement of the second register with the result 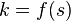where leads condition to

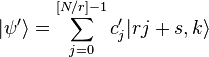Where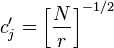

After measuring the state 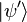the first register consists only of the basis vectors of the form 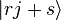such that 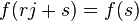for all 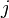. Therefore, it has a discrete homogeneous spectrum. Can't get a period right or a multiple of it, measuring the first register, because here - random value. Here we apply the discrete Fourier transform of the form

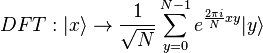on the register, since the probability of the spectrum in the transformed state is invariant with respect to the displacement (only the phases can be transformed, not the absolute values ​​of the amplitudes).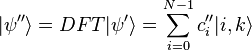

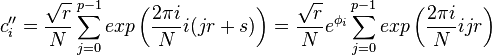
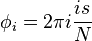Where and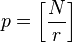

If a 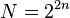multiple then 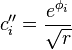, if a 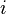multiple 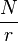and 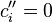otherwise. Even not a power of 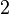then spectrum 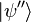shows individual peaks with a period 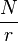, because

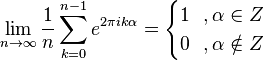
For the first register is used 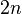qubit when 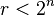because it guarantees at least 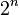elements in the given amount, and thus the width of the peaks will be of the order of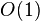

If we now calculate the first register, we get the value close to 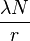where 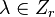. It can be written as 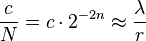It comes down to finding an approximation 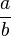where 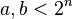for a particular binary point number Continued fractions are used to solve this problem.

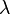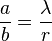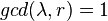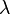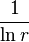Since the form of a rational number is not unique in its kind, and defined as , if a Probability that and simple more than so only 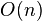Attempts need to be as close as possible to success. ^{[7] [5]} .