Lecture
The Grover algorithm (born Grover search algorithm , GSA) is a quantum algorithm for solving the search problem, that is, finding a solution to the equation
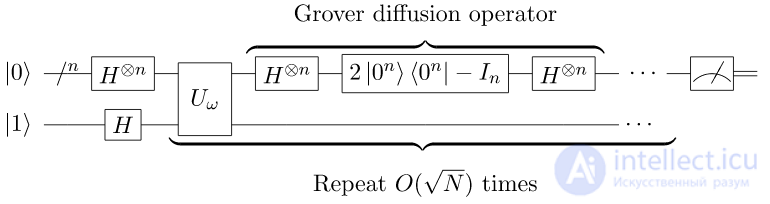
Grover's algorithm
Where 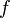 is a Boolean function of n variables. [one]
is a Boolean function of n variables. [one]
It is assumed that the function  given in the form of a black box, or an oracle, that is, in the course of a solution, we can only ask the oracle a question like: "what is
given in the form of a black box, or an oracle, that is, in the course of a solution, we can only ask the oracle a question like: "what is 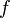 on this
on this 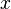 ", And after receiving the answer to use it in further calculations. That is, the problem of solving equation (1) is a general form of the enumeration problem; here you need to find the "password to the device
", And after receiving the answer to use it in further calculations. That is, the problem of solving equation (1) is a general form of the enumeration problem; here you need to find the "password to the device 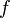 "That classically requires brute force all
"That classically requires brute force all 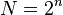 options.
options.
The GSA finds any root of the equation using 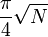 function calls
function calls 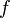 , using
, using 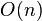 qubits. [2] The algorithm was discovered by the American mathematician Lov Grover in 1996.
qubits. [2] The algorithm was discovered by the American mathematician Lov Grover in 1996.
If equation (1) has 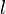 roots, according to the scheme of Grover, you can find one of them on a quantum computer during
roots, according to the scheme of Grover, you can find one of them on a quantum computer during 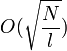 (even
(even 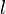 not known in advance), that is, the basic quantum complexity is the square root of the classical.
not known in advance), that is, the basic quantum complexity is the square root of the classical.
The classical algorithm for solving such a problem (linear search) obviously requires 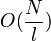 appeals to
appeals to 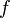 . The Grover algorithm allows us to solve the search problem in the time of the order of the square root of the classical one, which is a tremendous acceleration. GSA is proven to be optimal in the following ways:
. The Grover algorithm allows us to solve the search problem in the time of the order of the square root of the classical one, which is a tremendous acceleration. GSA is proven to be optimal in the following ways:
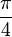 cannot be improved [3] .
cannot be improved [3] .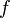 [4] .
[4] .The GSA is an example of a mass task dependent on an oracle. For more particular problems, it is possible to obtain greater quantum acceleration. For example, Shor’s factorization algorithm yields an exponential gain compared to the corresponding classical algorithms.
The fact that f is given in the form of a black box does not affect in general the complexity of both quantum and classical algorithms. Knowledge of the “device” of the function f (for example, knowledge of its defining scheme of functional elements) generally cannot help in solving equation (1). A database search corresponds to the inverse of a function that takes a specific value if the argument x corresponds to the required record in the database.
Let be 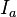 there is a unitary operator that mirrors the Hilbert space with respect to the hyperplane perpendicular to the vector
there is a unitary operator that mirrors the Hilbert space with respect to the hyperplane perpendicular to the vector 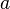 ,
, 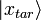 - the state corresponding to the root of equation (1),
- the state corresponding to the root of equation (1), 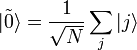 - uniform superposition of all states. Then GSA consists in applying the operator
- uniform superposition of all states. Then GSA consists in applying the operator 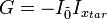 to the state
to the state 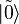 number of times equal to the integer part
number of times equal to the integer part 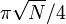 . The result will almost coincide with the state
. The result will almost coincide with the state 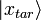 .
.
 . The quantum algorithm finds a maximum of
. The quantum algorithm finds a maximum of 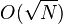 appeals to f .
appeals to f .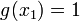 where
where 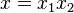 split line
split line 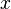 two rows of the same length. The algorithm has a complexity of the order of the square root of the classical time.
two rows of the same length. The algorithm has a complexity of the order of the square root of the classical time.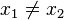 on which function
on which function  takes the same value. The algorithm requires
takes the same value. The algorithm requires 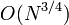 appeals to f .
appeals to f .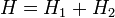 where
where 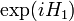 and
and 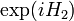 are operators
are operators 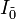 and
and 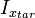 respectively. Then continuous unitary evolution with Hamiltonian
respectively. Then continuous unitary evolution with Hamiltonian 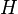 starting from
starting from 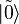 naturally leads to
naturally leads to 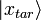 . The complexity of such a continuous GSA analog is exactly the same as for the discrete case.
. The complexity of such a continuous GSA analog is exactly the same as for the discrete case.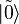 under the action of the Hamiltonian depending on f , according to the adiabatic theorem, for a time on the order of
under the action of the Hamiltonian depending on f , according to the adiabatic theorem, for a time on the order of 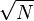 leads to state
leads to state 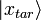 .
.The meaning of GSA is to “amplitude jump” (amplitude amplification) of the target state by decreasing the amplitude of all other states. Geometrically, the GSA consists in rotating the current state vector of a quantum computer in the direction exactly to the target state (moving along the shortest path ensures the GSA is optimal). Each step gives a rotation at an angle. 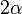 where is the angle between
where is the angle between 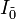 and
and 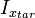 makes up
makes up  . Further continuation of the iterations of the operator G will continue the circumvention of the circle in the real plane generated by these vectors.
. Further continuation of the iterations of the operator G will continue the circumvention of the circle in the real plane generated by these vectors.
Grover's “amplitude jump” is apparently a fundamental physical phenomenon in the many-body quantum theory. For example, its accounting is necessary to estimate the probabilities of events that seem to be "rare". The process that implements the GSA scheme leads to an explosive growth of initially negligible amplitude, which can quickly bring it to actually observed values.
Grover’s algorithm can also be used to find the median and arithmetic mean of a number series. In addition, it can be used to solve NP-complete problems by exhaustive search among a variety of possible solutions. This may entail a significant increase in speed compared to classical algorithms, although not providing a “polynomial solution” in general.
Comments
To leave a comment
Quantum informatics
Terms: Quantum informatics