Quantum algorithm

A quantum algorithm is an algorithm designed to run on a quantum computer.

A quantum algorithm is a classical algorithm that defines a sequence of unitary operations (gates, or gates) with an indication of exactly which qubits they should be performed. A quantum algorithm is specified either in the form of a verbal description of such commands, or by using their graphical record in the form of a quantum gate array.

The result of the quantum algorithm is of a probabilistic nature ^[1] . Due to a small increase in the number of operations in the algorithm, one can arbitrarily approximate the probability of getting the correct result to unity.

The sets of problems that can be solved on a quantum computer and on a classical computer are the same. A quantum computer, therefore, does not increase the number of algorithmically solvable problems. The whole point of using a quantum computer is that it can solve some problems much faster than any of the classical ones. For this, the quantum algorithm must generate and use entangled quantum states in the course of the computation (see Quantum Superposition and Quantum Interlocking).

Any problem solved by a quantum algorithm can also be solved by a classical computer by directly calculating unitary matrices of exponential dimension, obtaining the explicit form of quantum states. In particular, problems that cannot be solved on classical computers (for example, the problem of stopping) remain unsolvable on quantum ones. But such direct modeling requires exponential time, and therefore the possibility arises, using quantum parallelism, to accelerate some classical algorithms on a quantum computer ^[2] .

Acceleration on a quantum computer is not related to the processor clock speed. It is based on quantum parallelism. One quantum computing step does a lot more work than a single classic step. However, it would be a mistake to equate a quantum computation with a parallel classical one. For example, a quantum computer cannot solve the enumeration problem faster than in 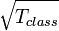Where 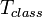- the running time of the deterministic classical search algorithm (see ^[3] ), while the non-deterministic classical algorithm solves it in time 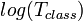. But a non-deterministic classical algorithm requires an exponential memory resource, that is, it is not physically feasible, whereas a quantum algorithm does not contradict the known laws of nature.

Quantum computing is a special kind of process. It uses a special physical resource: quantum entangled states, which allows in some cases to achieve an amazing gain in time. Such cases are called quantum acceleration of classical calculations.

Cases of quantum acceleration, against the background of the total mass of classical algorithms, are very rare (see ^[4] ). However, this does not detract from the fundamental importance of quantum computations, because they are capable of accelerating in principle the fulfillment of reusable type tasks.

Basic quantum acceleration schemes

The main type of tasks that are accelerated by quantum algorithms are brute force problems. They can be divided into 2 main groups:

1. The tasks of modeling the dynamics of complex systems (Feynman's original idea) and
2. Mathematical problems, which are reduced to the enumeration of options:
   1. The general case of iteration: Grover’s scheme and its variants, as well as
   2. Tasks of the search for hidden periods: Shor's scheme of using the fast quantum Fourier transform, and its analogues.

Type 1) is represented by the Zalka-Wiester algorithm for modeling unitary dynamics of quantum systems 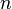particles in almost real time and with linear 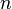by memory. This algorithm uses the Shore quantum Fourier transform circuit.

Type 2) is represented by:

• the Grover algorithm of the general search problem and its continuous and adiabatic variants, as well as algorithms using the Grover scheme: structured search (Fari, Gutman), extremum search algorithm (Hoyer, etc.) and search for matching lines in the database (Ambainis),
• Shor's algorithm for factoring integers, the Abrams-Lloyd algorithm for determining the period, the Kitaev algorithm for determining hidden subgroups, etc.

Type 1) is of the greatest interest from the point of view of further applications of a quantum computer.

Classification

Classification of quantum algorithms can be carried out according to the type of quantum transformations used by the algorithm. Among the commonly used transformations are: en: phase kick-back, phase estimation, en: quantum fourier transform, en: quantum walk, en: amplitude amplification, en: topological quantum field theory. It is also possible to group quantum algorithms by the type of problems they solve. ^[five]

Widely known algorithms

• Shor Algorithm
• Grover's algorithm
• Deutsch-Yozhi Algorithm

see also

• Quantum computer
• Quantum programming
• Algorithm List
• BQP class