Lecture
Algorithm Zalka - Wisner - designed to simulate the unitary dynamics of a quantum system 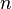 particles on a quantum computer. Unitary dynamics is a solution to the Schrödinger equation
particles on a quantum computer. Unitary dynamics is a solution to the Schrödinger equation
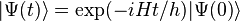
where is the Hamiltonian
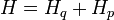
there is a sum of kinetic operators
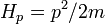
and potential
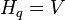
energies Algorithm Zalka - Wisner is a consistent application 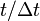 alternately two operators corresponding to these energies:
alternately two operators corresponding to these energies:
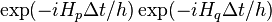 ,
, what gives the state 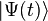 real system at time t, provided
real system at time t, provided 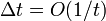 .
.
The operator corresponding to the potential energy 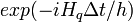 implemented on a quantum computer directly, since it has a diagonal shape. The kinetic energy operator must be pre-diagonalized using quantum Fourier transform.
implemented on a quantum computer directly, since it has a diagonal shape. The kinetic energy operator must be pre-diagonalized using quantum Fourier transform.
The Zalka-Wisner algorithm uses the Trotter formula, resulting from the expansion of the exponent to the second term, to represent the evolution operator. This gives a simulation in a time quadratic in comparison with the time of the actual process: 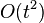 . Using the following terms of the exponential expansion gives a more efficient time-consuming simulation algorithm.
. Using the following terms of the exponential expansion gives a more efficient time-consuming simulation algorithm. 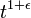 where is a positive constant
where is a positive constant  can be made arbitrarily small. Thus, the Zalka-Wisner scheme is able to simulate the states of a quantum system
can be made arbitrarily small. Thus, the Zalka-Wisner scheme is able to simulate the states of a quantum system 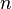 particles in almost linear time using memory
particles in almost linear time using memory 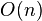 .
.
Simulation of quantum systems on a classical computer is impossible due to the fact that the dimension of the state space of a real quantum system grows as an exponent of the number of particles in it (see Quantum Computer). Therefore, the Zalka-Wisner algorithm implements the main idea of a quantum computer — to serve as a model for any multi-particle quantum system. Almost linear simulation time and linear memory means that a quantum computer, if it is built, will be able to simulate the evolution of the most complex systems (biomolecules, and, therefore, life) from first principles.
Simulation of a quantum system on a quantum computer has a different meaning than the so-called quantum-mechanical calculations on ordinary computers, in which we clearly get the amplitudes 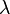 corresponding to the state
corresponding to the state 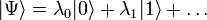 . When modeling on a quantum computer, we do not get the amplitudes themselves, but only the state itself
. When modeling on a quantum computer, we do not get the amplitudes themselves, but only the state itself 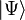 in its qubit discrete approximation. To obtain the amplitudes themselves, it is necessary to repeat the algorithm of quantum simulation many times and measure the resulting state, that is, to implement quantum tomography. Simulation on a quantum computer gives less than simulation on a regular computer would give, but the latter is impossible for complexity reasons. If we could model the dynamics of any quantum system on a conventional computer with the available complexity, then we could also simulate a process of fast quantum computation which is impossible due to the well-known lower bounds for quantum complexity.
in its qubit discrete approximation. To obtain the amplitudes themselves, it is necessary to repeat the algorithm of quantum simulation many times and measure the resulting state, that is, to implement quantum tomography. Simulation on a quantum computer gives less than simulation on a regular computer would give, but the latter is impossible for complexity reasons. If we could model the dynamics of any quantum system on a conventional computer with the available complexity, then we could also simulate a process of fast quantum computation which is impossible due to the well-known lower bounds for quantum complexity.
Modeling complex quantum systems necessarily requires the implementation of a quantum computer in one form or another.
Comments
To leave a comment
Quantum informatics
Terms: Quantum informatics