Representation of knowledge in intellectual systems. Production Systems and Logical Approach

Production systems

Representation of simple facts in logical systems

Examples of applying logic to knowledge representation

 

Production systems

Products along with frames are the most popular means of knowledge representation in AI. Products, on the one hand, are close to logical models, which allows them to organize effective withdrawal procedures, and, on the other hand, they more clearly reflect knowledge than classical logical models. There are no hard limitations typical of logical calculus, which makes it possible to change the interpretation of the elements of production.

Components of production systems

In general terms, a product is an expression of the following form: (i); Q; P; A Yu B; N.

Here i is the name of the product with which this product is distinguished from the entire set of products. The name may be a certain lexeme, reflecting the essence of this product (for example, "buying a book"), or the sequence number of products in their set, stored in the system's memory.

The element Q characterizes the scope of production. Such areas are easily distinguished in human cognitive structures. Our knowledge is "laid out on the shelves." Knowledge of how to prepare food, on the other how to get to work, etc. is stored on one shelf. The division of knowledge into separate areas allows you to save time on finding the right knowledge. The same division into spheres in the AI ​​knowledge base is also advisable when production models are used to represent knowledge.

The main element of the product is its core: A Yu B. Interpretation of the core of the product may be different and depends on what is to the left and to the right of the sign of the U sequence . The usual reading of the product core looks like this: IF A, TH, more complex kernel constructions allow an alternative choice on the right, for example IF A, TH B 1, ELSE B2. The sequence can be interpreted in the usual logical sense as a sign of the logical following of B from true A (if A is not a true expression, then nothing can be said about B). Other interpretations of the production core are also possible, for example, A describes some condition necessary for the action B to be taken.

Element P is a condition for the applicability of the core products. Usually P is a logical expression (usually a predicate). When P becomes true, the production core is activated. If P is false, then the core of the product cannot be used.

The element N describes the postconditions of the product. They are updated only if the core of the product is realized. The postconditions of the extension describe the actions and procedures that must be performed after the implementation of B. The execution of N can occur immediately after the implementation of the product core.

If a set of products is stored in the system's memory, then they form a production system. In the production system, special product management procedures should be specified, with the help of which the products are updated and the choice to perform one or another product from the number of actualized products. A number of AI systems use a combination of network and production knowledge representation models. In such models, declarative knowledge is described in the network component of the model, and procedural knowledge is described in the production component. In this case, talk about the work of the production system on the semantic network.

Classification of product cores.

Product cores can be classified for various reasons. First of all, all kernels are divided into two large types: deterministic and non-deterministic. In deterministic kernels, when the kernel is updated and if A is feasible, the right-hand side of the kernel is necessarily executed in non-deterministic kernels B may or may not be executed. Thus, the sequence of Ю in deterministic kernels is realized with necessity, and in non-deterministic kernels - with possibility. The interpretation of the core in this case may, for example, look like this: IF A, THEN IS POSSIBLE V.

The capability may be determined by some estimates of the kernel implementation. For example, if the probability of fulfillment B is given when A is updated, the output may be as follows: IF A, THEN WITH A PROBABILITY, REALIZE B. The core implementation estimate may be linguistic, associated with the term-set term of a linguistic variable, for example: IF A, TH MORE SHARES OF CONFIDENCE B. Other ways of implementing the kernel are possible.

Deterministic products can be unambiguous and alternative. In the second case, alternative choices are indicated on the right side of the kernel, which are evaluated by special choice weights. As such weights, probabilistic evaluations, linguistic evaluations, expert evaluations, etc. can be used.

A special type are predictive products, which describe the consequences expected during the actualization of A, for example: IF A, THEN WITH PROBABILITY, IT CAN BE EXPECTED B.

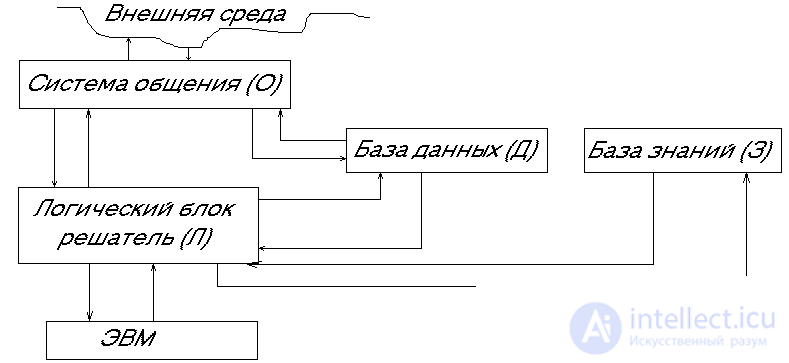
Further classification of production nuclei can be carried out based on the standard FIC scheme (Fig. 1). If x and y denote any of the blocks of the figure (O, D, 3, L), then the core Аx and By means that information about A is taken from x, and the result of triggering output B sends to block y. Combinations of x and y, meaningful from the point of view of FIC, are noted in Table 1 by the sign "+"

Table 1

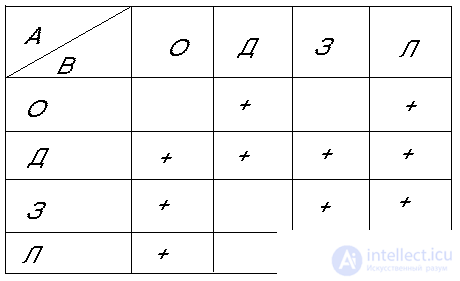
Pic 1

Consider a common type of product A3 Yu B3. In this case, A3 and B3 are some pieces of information stored in the knowledge base. With the network representation, it can be fragments of a semantic network, with logical models - the formulas of one or another calculus. Then the meaning of A3 Yu B3 products is to replace one fragment of the knowledge base with another. To update this product, it is necessary that a fragment exists in the knowledge base coinciding with A. When searching for knowledge base, A plays the role of a model, and the procedure for such a peep is called a pattern-based search.

Search organization decision strategies

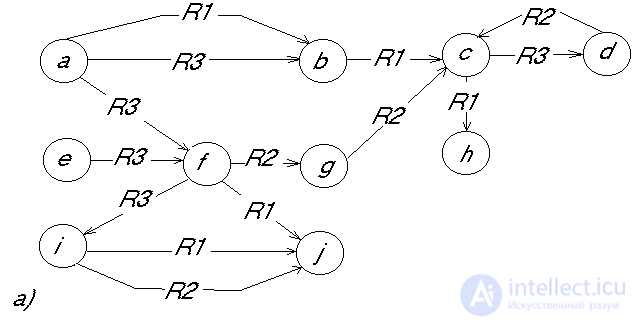
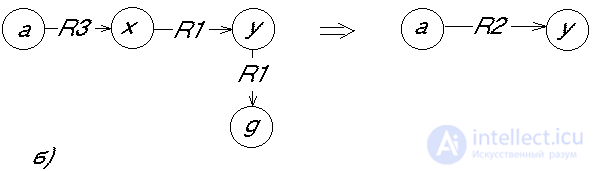
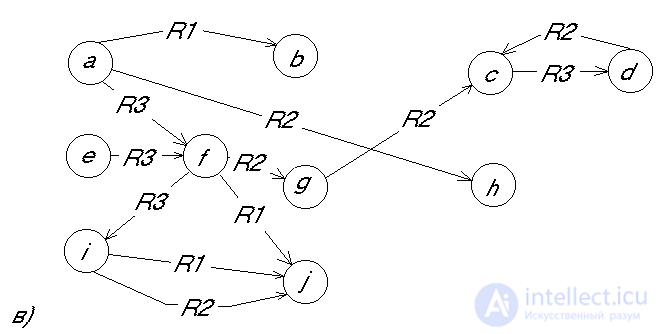
To illustrate the search, we assume that the knowledge base uses a semantic network (Fig. 2a) and products (Fig. 2b) for knowledge representation. Search A in the knowledge base is organized in various ways. You can, for example, first look for the vertex a. If there is no such vertex in the knowledge base, the search ends in failure. If the vertex a is found, then all arcs going out of it are marked with the relation R3, since in the sample to the right of this arc there is a vertex x whose place in the knowledge base can be any vertex. If no arc comes out of a, marked by the relation R3, then the search fails. But if there are such arcs, then a transition occurs to all the vertices with which the vertex a is connected by the relation R3, i.e. there is a parallel search process. In the example, there will be a transition from the vertex a to the vertices b and f, from which the search begins for the arcs emerging from them, marked by the relation R1 leading to any vertex, since the sample then has a vertex corresponding to the free variable y. Then the process continues in a similar way. In the example, the search is successful. After finding A in the semantic network, a replacement occurs, which is determined by the right side of the sample. As a result, a transformed network arises (Fig. 2c).

Products Ad Yu Vz can correspond to the procedure for finding patterns by empirical data. The logical block, on the basis of viewing and analyzing data, puts forward hypotheses and the presence of regularities and, having convinced of their acceptability and sufficient validity, writes them into the knowledge base. Similarly, we can interpret other types of products from table 1.

Presentation of simple facts

A representation is an action that makes a certain concept perceived by means of a figure, a recording, a language, or a formalism. The theory of knowledge studies the relationship between the subject (the student) and the object. Knowledge (in an objective sense) is what is known (what we know after studying).

Representation of knowledge - the formalization of true beliefs through figures, records or languages. We are especially interested in formalization, perceived (recognizable) computers. The question arises about the representation of knowledge in computer memory, i.e. about the creation of languages ​​and formalisms of knowledge representation. They transform a visual representation (created by speech, image, natural language, such as English or German, formal language, such as algebra or logic, reasoning, etc.) into suitable for input and processing in a computer. The result of the formalization should be a set of instructions that are part of the programming language.

The knowledge representation has a passive aspect: a book, a table, a memory filled with information. The AI ​​emphasizes the active aspect of representation: to know must become an active operation, allowing not only to memorize, but also to extract perceived (acquired, learned) knowledge for reasoning on their basis. Consequently, the origins of knowledge representation are in the science of knowledge, and its ultimate goal is informatics software. In many cases, the knowledge to be presented relates to a rather limited field, for example:

- description of the human condition

- a description of the situation in the game (for example, the location of the pieces in chess)

- description of the location of the personnel of the enterprise

- landscape description

To characterize a certain area, they talk about the "area of ​​reasoning" or "area of ​​expertise." Numerical formalization of such descriptions is generally not very effective. On the contrary, the use of a symbolic language, such as the language of mathematical logic, makes it possible to formulate descriptions in a form that is simultaneously close to both an ordinary language and a programming language. However, mathematical logic allows reasoning based on acquired knowledge: logical conclusions are indeed active operations for obtaining new knowledge from the learned.

For all these reasons, mathematical logic underlies various representations in AI. This section is devoted to the presentation of simple facts using predicate logic. The logical representation also serves as a starting point for other representations (such as "network" and "objective") used in AI.

Predicate logic syntax.

The language of predicate logic is defined by syntakis. For knowledge representation, the basic syntactic categories of the language are depicted by such characters that carry sufficiently clear information and give a fairly clear picture of the area of ​​reasoning (expertise).

Predicate logic, also called first-order logic, allows four types of expressions.

• Constants. They serve as the names of individuals (as opposed to the names of aggregates): objects, people, or events. Constants are represented by characters like Jacques_2 (appendix 2 to the word Jacques indicates a well-defined person among people with that name), Book_ 2 2, Parcel_8.

• Variables. Indicate the names of aggregates, such as person, book, package, event. The symbol Book_22 represents a well-defined instance, and the symbol book indicates either a set of "all books" or a "concept of a book." The symbols x, y, z represent the names of aggregates (certain sets or concepts).
• Predicative names. They define rules for connecting constants and variables, such as grammar rules, procedures, mathematical operations. For predicative names, characters like the following are used: Phrase, Send, Write, Plus, Divide. The predicate name is otherwise called the predicate constant.
• Functional names represent the same rules as predicates. In order not to be confused with predicate names, functional names are written in lower case letters: phrase, send, write, plus, divide. They are also called functional constants.

The symbols that are used to represent constants, variables, predicates, and functions are not “words of the Russian language”. They are the symbols of a certain representation - the words "object language" (in our case, the language of predicates).

The presentation should eliminate any ambiguity of the language. Therefore, the names of individuals contain numbers attributed to the names of the aggregates. Jacques_1 and Jacques_2 represent two people with the same name. These representations are the essence of the specification of the name "Jacques". A predicate is a predicate name along with a suitable number of terms. The predicate is also called the predicate form.

Examples of the application of logic to the representation of knowledge.

We illustrate the syntax of predicate logic by matching several Russian phrases with their translation into the language of logical formalism.

- In Russian: Jacques sends the book to Marie ,

Logically: the Package (Jacq_2, Mari_4, Kniga_22 ).

- In Russian: Everyone is walking,

Logically: " x ( Man ( x) É Strolls (x)).

- According to Russian: Some people walk ,

Logically: $ x ( Man (x) Ù Walking ( x)).

( Comparing the last two examples, we see that replacing the adjective " each " with " some " entails, when translating, not only replacing the quantifier " with $ , but replacing the bunch É with. This illustrates the fact that the translation of a natural language phrase into a logical one, speaking, is not a stencil process. )

In Russian: No one walks,

Logically: Ø ( $ x ( Man ( x) Walking (x))).