Non-Markov process

A non-Markov process is a random process whose evolution after any given time value 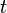depends on the evolution preceding this point in time. In other words, the “future” of the non-Markov process depends on its “past.” A non-Markov process is a random process with memory, while speaking of the memory of a process, it is meant that its statistical characteristics in the future depend on the nature of the evolution of a process in the past. The non-Markov process is contrasted with the Markov process.

Examples of non-Markov processes

An example of a non-Markov process is flicker noise observed in systems of different physical nature ^[1] . In particular, the experimentally observed fluctuations of kinetic coefficients (for example, fluctuations of the coefficient of electrical conductivity) have a spectral density characteristic of flicker noise. Flicker noise is the main type of noise that limits the sensitivity of electronic devices in the low-frequency part of the spectrum ^[2] . We also note that the influence of a Markov process on any dynamic system leads to the fact that its response is, in general, a non-Markov process. The sum of two Markov processes, generally speaking, is a non-Markov process. Non-Markov processes will also be those formed in Markov’s integration. In particular, the coordinate of a Brownian particle, equal to the integral of its velocity, is generally not described by the Markov process model. The Wiener approximation for Brownian motion is valid only for sufficiently long time intervals, which are significantly longer than the particle relaxation time. At small time intervals, the Brownian motion is fundamentally non-Markov. The class of non-Markov processes includes real radio-technical signals with their amplitude and phase modulation by a combination of deterministic and random processes ^[3] . The increments for such signals have a non-Gaussian probability distribution, are not correlated, and are statistically dependent.

A typical random process — the Brownian motion of a particle in a viscous medium — also, generally speaking, belongs to the class of non-Markov processes ^{[4] [5]} . In fact, a Brownian particle, moving in a viscous medium, entrains the surrounding particles of the medium, which in turn begin to influence the Brownian particle. This effect depends on the nature of the motion of the particles of the medium, which in turn depends on how the Brownian particle moved earlier. Thus, the motion of a Brownian particle is affected by its entire past behavior in a viscous medium. This effect is especially noticeable at small time intervals and in the case of small particles (submicron and nanometer size) ^[6] . Non-Markov, for example, will be fluctuations of the luminescence intensity, if external excitation to the phosphor is subject to white or shot noise ^[7] .

Fundamentally non-Markov processes are random processes in complex systems. These include stock price fluctuations, changes in the average temperature of the Earth and other processes.

Description of non-Markov processes

The description of non-Markov processes using a well-developed theory of stochastic differential systems that uses stochastic differential equations, for example, the Fokker – Planck equation, can only be approximate. This is due to the fact that differential equations connect quantities at a given time and cannot take into account the memory of a non-Markov process. A non-Markov process can, in principle, be described using integral stochastic equations, which allow to take into account the hereditary properties of the process ^[8] .