Markov process

The Markov process is a random process, the evolution of which after any given value of the time parameter 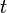does not depend on the evolution preceding 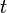, provided that the process value at this moment is fixed (the “future” of the process does not depend on the “past” with the known “present”; another interpretation (Wentzel): the “future” of the process depends on the “past” only through the “present”).

The Markov process — a first order autoregression model of AR (1): x _t = ₁ * x _t-1 + ε _t

History

The property defining a Markov process is called a Markov property; It was first formulated by A. A. Markov, who, in the works of 1907, initiated the study of sequences of dependent tests and related sums of random variables. This line of research is known as Markov chain theory.

However, in the work of L. Bachelier, one can see an attempt to interpret the Brownian movement as a Markov process, an attempt that was justified after Wiener's research in 1923.

The foundations of the general theory of Markov processes with continuous time were laid by Kolmogorov.

The difference of the Markov process from the Markov chain

Markov chain with discrete time - time is discrete, state space is discrete.

Markov chain with continuous time - time is continuous, the state space is discrete.

The Markov process is both time and state space continuously.

Markov property

General case

Let be 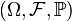- probabilistic space with filtering 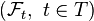over some (partially ordered) set 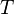; let it go 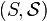- Sigma-algebra. Random process 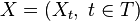defined on a filtered probability space is considered to satisfy the Markov property if for each 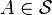and ,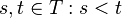

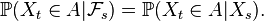
The Markov process is a random process that satisfies the Markov property with natural filtration.

For Markov chains with discrete time

If 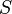is a discrete set and 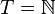The definition can be reformulated:

.

An example of a Markov process

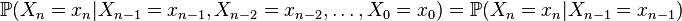Consider a simple example of a Markov random process. A point randomly moves along the abscissa. At time zero, the point is at the origin and remains there for one second. After a second, a coin rushes - if a coat of arms has fallen, then point X moves one unit of length to the right, if the figure - to the left. A second later, the coin rushes again and the same random movement is made, and so on. The process of changing the position of a point (“wandering”) is a random process with discrete time (t = 0, 1, 2, ...) and a countable set of states. Such a random process is called Markov, since the next state of a point depends only on the current (current) state and does not depend on past states (no matter which way and for what time the point fell into the current coordinate).