Lecture
The chain of Markov is a sequence of random events with a finite or countable number of outcomes, characterized by the property that, speaking loosely, with a fixed present, the future is independent of the past. Named in honor of A. A. Markov (senior).
Sequence of discrete random variables 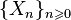 called a simple Markov chain (with discrete time) if
called a simple Markov chain (with discrete time) if
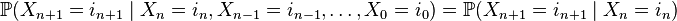 .
.
Thus, in the simplest case, the conditional distribution of the subsequent state of the Markov chain depends only on the current state and does not depend on all previous states (unlike the Markov chains of higher orders).
Range of values of random variables 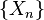 called the chain space , and the number
called the chain space , and the number 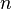 - step number.
- step number.
Matrix 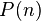 where
where
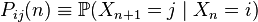
is called the matrix of transition probabilities on 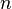 m step and vector
m step and vector 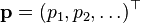 where
where
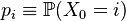
- the initial distribution of the Markov chain.
Obviously, the transition probability matrix is stochastic, that is,
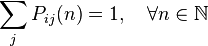 .
.
A Markov chain is said to be single -pitch if the transition probability matrix does not depend on the step number, that is,
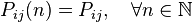 .
.
Otherwise, the Markov chain is called inhomogeneous. In the following, we will assume that we are dealing with homogeneous Markov chains.
From the properties of conditional probability and the definition of a homogeneous Markov chain we get:
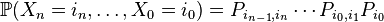 ,
,
whence the special case of the Kolmogorov – Chapman equation follows:
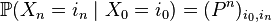 ,
,
that is, the transition probability matrix for 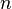 steps of a homogeneous Markov chain
steps of a homogeneous Markov chain 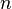 -th degree of the matrix of transition probabilities for 1 step. Finally,
-th degree of the matrix of transition probabilities for 1 step. Finally,
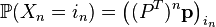 .
.
Family of discrete random variables 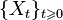 called a Markov chain (with continuous time) if
called a Markov chain (with continuous time) if
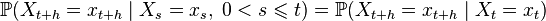 .
.
A chain of Markov with continuous time is called homogeneous if
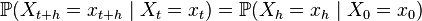 .
.
Similar to the discrete time case, the finite-dimensional distributions of a homogeneous Markov chain with continuous time are completely determined by the initial distribution
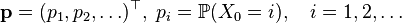
and the matrix of transition functions ( transition probabilities )
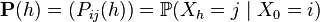 .
.
The matrix of transition probabilities satisfies the Kolmogorov – Chapman equation: 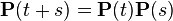 or
or
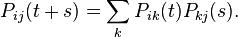
By definition, the intensity matrix 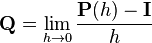 or equivalently
or equivalently
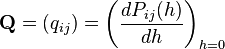 .
.
From the Kolmogorov-Chapman equation, two equations follow:
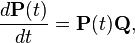
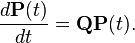
For both equations, the initial condition is chosen 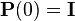 . Appropriate solution
. Appropriate solution 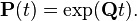
For anyone  matrix
matrix 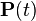 has the following properties:
has the following properties:
 non-negative:
non-negative: 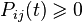 (nonnegative probability).
(nonnegative probability).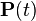 equals 1:
equals 1: 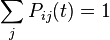 (total probability), that is, the matrix
(total probability), that is, the matrix 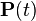 is stochastic on the right (or in rows).
is stochastic on the right (or in rows).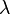 matrices
matrices 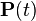 do not exceed 1 in absolute value:
do not exceed 1 in absolute value: 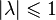 . If a
. If a 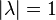 then
then  .
. matrices
matrices 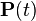 corresponds to at least one non-negative left eigenvector line (equilibrium):
corresponds to at least one non-negative left eigenvector line (equilibrium): 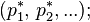
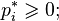
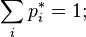
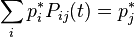 .
. matrices
matrices 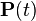 all root vectors are proper, that is, the corresponding Jordan cells are trivial.
all root vectors are proper, that is, the corresponding Jordan cells are trivial.Matrix 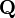 has the following properties:
has the following properties:
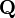 non-negative:
non-negative: 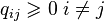 .
.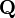 non-positive:
non-positive: 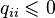 .
.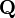 equals 0:
equals 0: 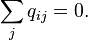
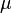 matrices
matrices 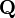 non-positive:
non-positive: 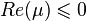 . If a
. If a 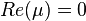 then
then 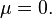
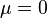 matrices
matrices 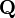 corresponds to at least one non-negative left eigenvector line (equilibrium):
corresponds to at least one non-negative left eigenvector line (equilibrium): 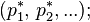
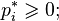
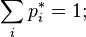
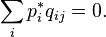
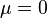 matrices
matrices 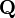 all root vectors are proper, that is, the corresponding Jordan cells are trivial.
all root vectors are proper, that is, the corresponding Jordan cells are trivial.For a Markov chain with continuous time, an oriented transition graph (briefly, a transition graph) is constructed according to the following rules:
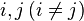 connected by oriented edge
connected by oriented edge 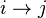 , if a
, if a 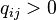 (i.e. the flow rate from
(i.e. the flow rate from 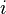 th state in
th state in 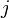 is positive.
is positive.Topological properties of the transition graph associated with the spectral properties of the matrix 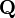 . In particular, the following theorems are true for finite Markov chains:
. In particular, the following theorems are true for finite Markov chains:
A. For any two different vertices of the transition graph 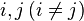 there is such a vertex
there is such a vertex 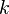 a graph (“common drain”) that there are oriented paths from the top
a graph (“common drain”) that there are oriented paths from the top 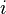 to the top
to the top 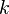 and from the top
and from the top 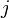 to the top
to the top 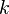 . Note : possible case
. Note : possible case 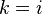 or
or 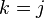 ; in this case, the trivial (empty) path from
; in this case, the trivial (empty) path from 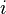 to
to 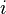 or from
or from 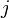 to
to 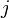 also considered an oriented way.
also considered an oriented way.
B. Zero eigenvalue of the matrix 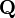 nondegenerate.
nondegenerate.
B. When 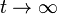 matrix
matrix 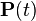 tends to the matrix, in which all the rows coincide (and coincide, obviously, with the equilibrium distribution).
tends to the matrix, in which all the rows coincide (and coincide, obviously, with the equilibrium distribution).
A. The transition graph of a chain is oriented.
B. Zero eigenvalue of the matrix 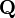 is non-degenerate and corresponds to a strictly positive left eigenvector (equilibrium distribution).
is non-degenerate and corresponds to a strictly positive left eigenvector (equilibrium distribution).
B. For some 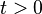 matrix
matrix 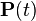 strictly positive (i.e.
strictly positive (i.e. 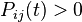 for all
for all 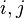 ).
).
G. For all 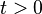 matrix
matrix 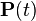 strictly positive.
strictly positive.
D. When 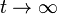 matrix
matrix 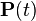 tends to a strictly positive matrix, in which all the rows coincide (and obviously coincide with the equilibrium distribution).
tends to a strictly positive matrix, in which all the rows coincide (and obviously coincide with the equilibrium distribution).

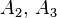 ); b) weakly ergodic, but not ergodic chain (transition graph is not oriented connected); c) ergodic chain (transition graph orientedly connected).
); b) weakly ergodic, but not ergodic chain (transition graph is not oriented connected); c) ergodic chain (transition graph orientedly connected).Let us consider Markov chains with three states and with continuous time, corresponding to the transition graphs shown in Fig. In case (a), only the following nondiagonal elements of the intensity matrix are nonzero: 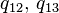 in case (b) are non-zero only
in case (b) are non-zero only 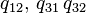 , and in case (c) -
, and in case (c) - 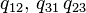 . The remaining elements are determined by the properties of the matrix.
. The remaining elements are determined by the properties of the matrix. 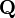 (the sum of the elements in each row is 0). As a result, for graphs (a), (b), (c), the intensity matrices are:
(the sum of the elements in each row is 0). As a result, for graphs (a), (b), (c), the intensity matrices are: 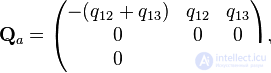
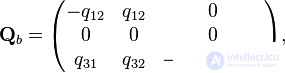
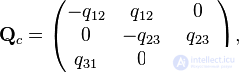
The basic kinetic equation describes the evolution of the probability distribution in a Markov chain with continuous time. The “basic equation” here is not an epithet, but a translation of the term English. Master equation . For a probability distribution vector string 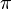 the basic kinetic equation is:
the basic kinetic equation is:
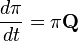
and coincides, essentially, with the direct Kolmogorov equation. In the physical literature, probability column vectors are used more often and the basic kinetic equation is written in the form that explicitly uses the law of conservation of total probability:
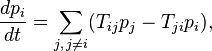
Where 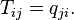
If for the basic kinetic equation there is a positive equilibrium 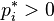 then it can be written in the form
then it can be written in the form
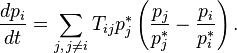
For the basic kinetic equation, there exists a rich family of convex Lyapunov functions — monotonously varying with time distribution probability functions. Let be 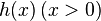 - convex function of one variable. For any positive probability distribution (
- convex function of one variable. For any positive probability distribution ( 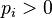 ) we define the function Morimoto
) we define the function Morimoto 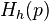 :
:
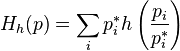 .
.
Derivative 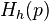 on time if
on time if 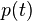 satisfies the basic kinetic equation, there is
satisfies the basic kinetic equation, there is
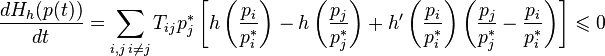 .
.
The last inequality holds because of the bulge 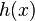 .
.
 [edit]
[edit]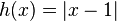 ,
, 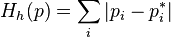 ;
;this function is the distance from the current probability distribution to the equilibrium in 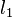 -norm The time shift is a contraction of the space of probability distributions in this norm. (For compression properties, see the Banach Fixed Point Theorem article.)
-norm The time shift is a contraction of the space of probability distributions in this norm. (For compression properties, see the Banach Fixed Point Theorem article.)
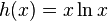 ,
, 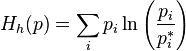 ;
;this function is (minus) Kullback entropy (see Kullback – Leibler Distance). In physics, it corresponds to the free energy divided by 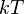 (Where
(Where 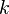 —Permanent Boltzmann,
—Permanent Boltzmann, 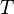 - absolute temperature):
- absolute temperature):
if a 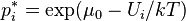 (Boltzmann distribution), then
(Boltzmann distribution), then
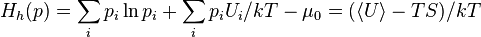 .
.
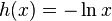 ,
, 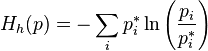 ;
;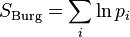
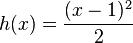 ,
, 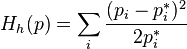 ;
;this is a quadratic approximation for the (minus) Kullback entropy near the equilibrium point. Up to a time-constant term, this function coincides with the (minus) Fisher entropy, which is given by the following choice,
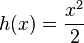 ,
, 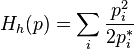 ;
;this is (minus) Fisher entropy.
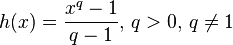 ,
, 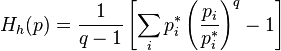 ;
;This is one of the analogues of free energy for the entropy of Tsallis. Tsallis entropy
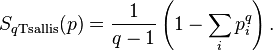
serves as the basis for the statistical physics of nonextensive quantities. With 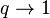 it tends to the classical Boltzmann – Gibbs – Shannon entropy, and the corresponding Morimoto function to the (minus) Kullback entropy.
it tends to the classical Boltzmann – Gibbs – Shannon entropy, and the corresponding Morimoto function to the (minus) Kullback entropy.
Comments
To leave a comment
probabilistic processes
Terms: probabilistic processes