Linear systems

A system is considered linear if its response to input signals is additive (the principle of superposition of signals is fulfilled) and homogeneous (the principle of proportional similarity is fulfilled). In other words, the response of a linear system to the weighted sum of input signals should be equal to the weighted sum of responses to individual input signals, regardless of their number and for any weighting factors , including complex ones.

With the software implementation of linear systems on a computer, as a rule, there are no special difficulties in ensuring linearity within reasonable limits of the values ​​of the input and output signals. With the physical (hardware) implementation of data processing systems, the range of input and output signals, in which the linearity of signal conversion is ensured, is always limited and must be specially stipulated.

Shift invariance of systems. A system is called shift-invariant if a shift of the input signal by arguments (time, space coordinates, etc.) causes a corresponding shift of the output signal:

y (x, t) = T [s (x, t)], T [s (x- D x, t- D t)] = y (x- D x, t- D t).

This means that the shape of the output signal depends only on the input signal, and does not depend on the time the signal arrives at the input of the system. The invariance of the system to a shift is one of the confirmations of the constancy of its parameters.

Shear invariant linear systems. Linearity and shear invariance are independent properties of systems and do not determine each other. So, for example, the operation of squaring a signal is shift invariant but nonlinear.

In the theory of data analysis and processing, the main place is occupied by systems that are linear and shear invariant (LIS - systems). They have fairly broad practical capabilities with the relative simplicity of the mathematical apparatus. In the future, if this is not specifically mentioned, we will mean just such systems.

The advantage given to LIS systems in information processing methods is based on the possibility of decomposing an input signal of any, arbitrarily complex, into components of the simplest forms, the response of the system to which is known and well studied, with the subsequent calculation of the output signal in the form of the sum of responses to all components of the input signal. As a rule, single impulses and harmonic components are used as the simplest forms of signal decomposition. The decomposition in terms of single impulses is used for dynamic presentation of a signal depending on real physical arguments (time, coordinates, etc.) and uses the convolution operation. Harmonic decomposition uses the spectral (frequency) representation of the signal and the Fourier transform.

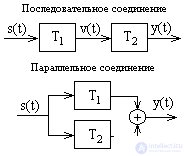
LIS connections - systems. When systems are connected in series (cascade), the output of one system serves as an input signal for the second, etc. depending on the number of components of the cascade systems. In relation to the general system transformation operation, the order of joining the systems included in it does not matter. So, for two series-connected systems in Fig. 1.3.2:

y (t) = T ₂ [T ₁ [s (t)]] = T ₁ [T ₂ [s (t)]].

With a parallel connection, the input signal is fed simultaneously to the inputs of all components of the systems, and the output signals of the systems are summed:

y (t) = T ₁ [s (t)] + T ₂ [s (t)] + ... + T _N [s (t)].

The systems formed as a result of connections as a whole are also LIS - systems if the systems included in them are linear and invariant to a shift.

The generalized diagram of the digital signal processing system in Fig. 1.3.3 is given as an example.

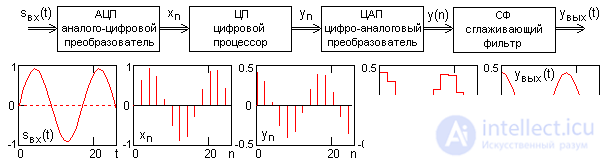
Figure: 1.3.3. Block diagram of the signal differentiation system.