Lecture
The degree of uncertainty of the state of an object (or the so-called source of information) depends not only on the number of its possible states, but also on the probability of these states. In unequal conditions, the freedom of choice for the source is limited. So, if of two possible states the probability of one of them is 0.999, then the probability of the other state is correspondingly equal to 1-0.999 = 0.001, and when interacting with such a source, the result is practically a foregone conclusion.
In the general case, in accordance with the theory of probabilities, the information source is uniquely and completely characterized by the ensemble of states U = {u 1 , u 2 , ..., u N } with state probabilities, respectively {р (u 1 ), р (u 2 ) , ..., р (u N )} provided that the sum of the probabilities of all states is equal to 1. The measure of the amount of information, as the uncertainty of the choice of a discrete source of a state from an ensemble U, was proposed by K. Shannon in 1946 and was called the entropy of a discrete source of information or the entropy of the final ensemble:
H (U) = - 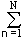 p n log 2 p n . (1.4.2)
p n log 2 p n . (1.4.2)
Shannon's expression coincides with Boltzmann's expression for the entropy of physical systems when assessing the degree of diversity of their states. The Shannon entropy measure is a generalization of the Hartley measure to the case of ensembles with non- equiprobable states , which is easy to see if in expression (1.4.2) the value of p n is replaced by the value p = 1 / N for an ensemble of equiprobable states. The entropy of a finite ensemble H (U) characterizes the uncertainty that falls on the average for one state of the ensemble.
Considering that in what follows in all mathematical expressions concerning entropy, we will use only the binary base of the logarithm, the index 2 of the base of the logarithm in the formulas will be assumed by default.
|
u i |
p i |
u i |
p i |
u i |
p i |
u i |
p i |
u i |
p i |
|
and |
.064 |
s |
.015 |
about |
.096 |
x |
.009 |
eh |
.003 |
|
b |
.015 |
and |
.064 |
P |
.024 |
c |
.004 |
Yu |
.007 |
|
in |
.039 |
th |
.010 |
R |
.041 |
h |
.013 |
I |
.019 |
|
r |
.014 |
to |
.029 |
from |
.047 |
w |
.006 |
- |
.124 |
|
d |
.026 |
l |
.036 |
t |
.056 |
u |
.003 |
|
|
|
her |
.074 |
m |
.026 |
at |
.021 |
b, b |
.015 |
|
|
|
f |
.008 |
n |
.056 |
f |
.020 |
s |
.016 |
|
|
Example. Calculate the entropy of an ensemble of 32 letters of the Russian alphabet. The probabilities of using letters are shown in the table. Compare entropy with the uncertainty that the alphabet would have if they were equally likely to be used .
Uncertainty by one letter with equal probability of use:
H (u) = log 32 = 5
Entropy of the alphabet by ensemble of the table:
H (u) = - 0.064 log 0.064 - 0.015 log 0.015 -. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... - 0.143 log 0.143 " 4.42.
Thus, the unevenness of the states reduces the entropy of the source.
Comments
To leave a comment
Signal and linear systems theory
Terms: Signal and linear systems theory