Information capacity of signals

The information capacity of signals depends significantly on the type of signals and determines the requirements for data transmission channels (communication channels), as well as the technical characteristics of communication channels determine the requirements for the information capacity of signals transmitted over these channels.

For discrete signal transmission channels (discrete communication channels), the concepts of technical and information data transmission rate are used.

The technical transmission rate refers to the number of chips (symbols) transmitted over the channel per unit of time. The simplest elementary symbol is a unipolar electrical pulse of duration t at the clock interval T. In discrete channels, as a rule, bipolar pulses are used, positive in the first half of the interval T and negative in the second half. This allows you to maintain the zero potential of the cable and perform clock synchronization of the transmission and reception of signals. The unit of measurement of the technical speed V _t = 1 / T is BOD - one symbol per second. The bandwidth of the communication channel is usually limited by a certain cutoff frequency F _beforeby the level of signal attenuation to the level of statistical noise, while the value of the technical data transmission rate, of course, cannot be higher than F _pre without any special devices for separating information signals.

With a known technical speed V _T, the information transfer rate is measured in bits per second, and at a noise level less than the amplitude values ​​of symbol pulses, it is given by the ratio:

V _h = V _t H (s),

where H (s) is the entropy of the symbol. For binary discrete symbols with possible states [0, 1] (unipolar - there is / no pulse per cycle, for bipolar - the order of polarity of pulses per cycle, for example, 0: plus / minus, 1: minus / plus) at a constant pulse amplitude value H (s) is 1. With the number L of possible equiprobable pulse amplitude levels (the noise level is less than the difference in the pulse amplitude levels), the value of H (s) is log L.

The information capacity of the signal or the total amount of information in the signal S (message, code sequence / word) is determined by the total number N = t / T of the entropy of symbols in bits at the signal setting interval t:

I _t (S) = N log L = (t / T) log L. (1.4.7)

An increase in the number of levels L increases the capacity of communication channels, but complicates the data coding equipment and reduces the noise immunity of communication.

For continuous signals, transmission via communication channels is possible only provided that the maximum information frequency in the signal F _max does not exceed the limiting frequency F _{before the} transmission of signals by the communication channel. To estimate the information capacity of a continuous signal, let us sample it with an interval D t = 1 / 2F _max . As established by Kotelnikov in 1933 , from instantaneous readings of a continuous signal with such a sampling interval, the analog signal can be restored without loss of information. For the full duration of the signal T _{s, the} number of samples is:

N = T _s / D t = 2F _max T _s .

Let us determine the maximum possible number of samples in each sample in the presence of noise in a channel with an average power P _w = d ² . With an average signal power P _s = s ² :

L = = .

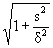Signal information capacity:

I (S) = 2F _max T _s log L. (1.4.8)

The informational capabilities of the signal increase with the expansion of its spectrum and the excess of its level over the noise level.