Dimension of signals

The simplest signals of geophysical practice are one-dimensional signals, such as seismic impulses s (t), measurements of any parameters of geophysical fields (electric, magnetic, etc.) along the profiles on the earth's surface s (x) or along the wellbore s ( h), etc. The values ​​of one-dimensional signals depend on only one independent variable, as, for example, in Fig. 1.1.1 and 1.1.2.

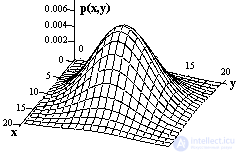
In the general case, signals are multidimensional functions of spatial, temporal and other independent variables - a seismic wave along the profile line s (x, t), an anomaly of the gravitational field on the observation surface s (x, y), the spatial - energy distribution of the flux of ionizing particles or quanta from radiation source s (x , y, z, E), etc. Multidimensional signals generated by a set of one-dimensional signals are also increasingly used, such as, for example, complex logging measurements of several physical parameters of rocks along a wellbore simultaneously.

Multidimensional signals can have different representations in their arguments. Thus, the total acoustic signal of the seismic profile is discrete in space (points of location of receivers) and continuous in time.

A multidimensional signal can be viewed as an ordered collection of one-dimensional signals. Taking this into account, when analyzing and processing signals, many principles and practical methods of processing one-dimensional signals, the mathematical apparatus of which is developed quite deeply, apply to multidimensional signals. The physical nature of signals for the mathematical apparatus of their processing does not matter.

At the same time, the processing of multidimensional signals has its own peculiarities, and can differ significantly from one-dimensional signals due to the greater number of degrees of freedom. So, when sampling multidimensional signals, not only the frequency spectrum of the signals is important, but also the shape of the sampling raster. An example of a not very useful feature is that multidimensional polynomials of signal functions, unlike one-dimensional ones, do not decompose into prime factors. As for the order of dimension of multidimensional signals, its increase above two practically does not change the principles and methods of data analysis, and affects, basically, only the degree of cumbersomeness of formulas and purely technical complication of calculations.

Considering these factors, when considering the general theory of analysis, transformations and signal processing, we will confine ourselves mainly to one- and two-dimensional signal functions, and as universal independent variables (function arguments) we will use, as a rule, the variable "t" for one-dimensional signals and variables "x, t" or "x, y" for two-dimensional signals, regardless of their physical content (space, time, energy, etc.).