Lecture
The general solution of a second-order inhomogeneous linear equation y "+ py '+ qy = f ( x ) is the sum of the general solution y 0 of the homogeneous equation and the particular solution y * of this equation, that is, y = y 0 + y * .
If the right side of the f ( x ) equation is the product of e α · x P n ( x ) , where α is a number, P n ( x ) is a polynomial of degree n , then the particular solution y * is found by selecting the indeterminate coefficients of the polynomial 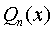 degrees n .
degrees n .
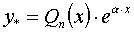 .
. 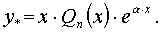
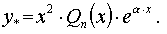
Let f ( x ) be:
where P ( x ) , R ( x ) are polynomials.
Let n be the greatest degree of these polynomials. The particular solution y * is found by selecting the indefinite coefficients of the polynomials U n ( x ) , V n ( x ) of degree n :
1) if the numbers a ± ib are not the roots of the characteristic equation k 2 + pk + q = 0 , then
2) if the numbers a ± ib are the roots of the characteristic equation k 2 + pk + q = 0 , then;
.
Choosing the form of the particular solution y * corresponding to the right side f ( x ) of the differential equation, we find y * ' , y * "
Substituting the expressions found for y * , y * ' , y * " into the original second-order linear equation, we determine the unknown coefficients of the polynomial 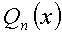 or the polynomials U ( x ) and V ( x ) .
or the polynomials U ( x ) and V ( x ) .
Comments
To leave a comment
Mathematical analysis. Differential equations
Terms: Mathematical analysis. Differential equations