Lecture
Example N 1
Find the general solution of the equation 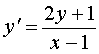 .
.
Decision.
Because 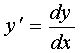 , the equation has the form:
, the equation has the form: 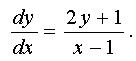
Multiplying the entire equation by dx , we get: 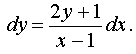
Dividing the whole equation by 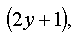 we arrive at an equation with separable variables:
we arrive at an equation with separable variables: 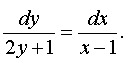
Integrating, we get:
Answer: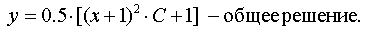
Example N 2
Find the general solution of the equation 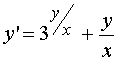 .
.
Decision.
The equation is homogeneous, since the function on the right-hand side is homogeneous:
.
Make the substitution: 
Transform the original equation:
Got an equation with separable variables: 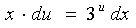 . Divide the equation by
. Divide the equation by 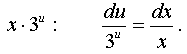
Integrating by term, we get:
Answer: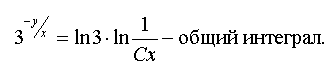
Example N 3
Find the general solution of the equation y ' + 3 x 2 y + x 2 = 0.
Decision.
The equation is linear with respect to the function y and its derivative y ' . We look for a solution in the form y = u · v , where u and v √ are functions of x . Because 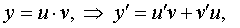 then the original equation takes the form:
then the original equation takes the form: 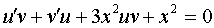 or
or 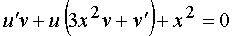 .
.
The function v is found from the equation 3 x 2 v + v ' = 0, while the original equation is simplified: u'v + x 2 = 0. Find the function v :
The function is found from the equation u'v + x 2 = 0 with 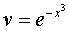 :
:
Answer: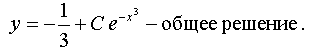
Example N 4
Solve the Cauchy problem: y "+ y = x , y (0) = 1, y ' (0) = 1.
Decision.This is a non-uniform linear equation with constant coefficients. Its solution is the sum of y 0 - the general solution of the equation y "+ y = 0 and y * - the particular solution of this equation.
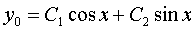 .
. 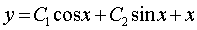 - common decision.
- common decision. Substituting the found constants С 1 and С 2 into a general solution, we obtain the solution of the Cauchy problem: 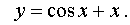
Answer: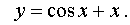
Example N 5
Find the general solution of the differential equation: 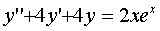 .
.
Decision.
The general solution of the original equation is equal to the sum of the general solution of the homogeneous equation y 0 and the particular solution y * .
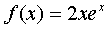 , ( α = 1 is not the root of the characteristic equation, the degree of the polynomial is equal to one), then we look for the particular solution y * in the form:
, ( α = 1 is not the root of the characteristic equation, the degree of the polynomial is equal to one), then we look for the particular solution y * in the form: 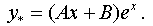
Substituting y * , y * ' , y * " into the original equation, we get:
Dividing by e x , after bringing similar ones we get:
Comparing the coefficients at the same degrees, we compose a system of linear algebraic equations:
finding a solution to this system:
write the general solution:
Answer: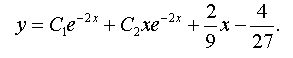
Comments
To leave a comment
Mathematical analysis. Differential equations
Terms: Mathematical analysis. Differential equations