4.1.3. Homogeneous differential equations

A first-order equation y ' = f ( x, y ) is called homogeneous with respect to x and y if the function f ( x, y ) is homogeneous: f ( λx, λy ) = f ( x, y ) .

A homogeneous function can be represented as a function of :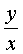

.

Using substitution 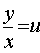(because 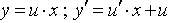) The differential equation y ' = f ( x, y ) reduces to an equation with separable variables: