Lecture
Introduction
At one time or another, most users were faced with building hierarchical information in an SQL database, and they realized that managing hierarchical data is clearly not the purpose of a relational database. Relational database tables are not hierarchical (similar to XML ), but simple flat lists. Hierarchical data has parent-child relationships that, naturally, are not represented in the relational database table.
In relational databases, storing information in the form of tree-like structures is a task with additional overhead. Such additional expenses can be either an increase in the number of requests or an increase in the amount of information that serves to organize the data structure.
Common approaches for organizing tree structures are:
|
Adjacency List |
The organization of the data structure is that each object stores information about the parent object, that is, there is an additional field in the row of the table that indicates the ID of the object in which the object is nested. |
| Nested set Nested set |
Nested sets store information not only about the so-called left and right keys, as well as the level of nesting. This version of the organization of the data structure is convenient for reading, but it is more difficult to modify. |
| Materialized Path Materialized way |
The idea of this data structure is that each record stores the full path to the root element of the tree. |
Consideration of these data structures was caused by the need to introduce comments (with a tree structure) for articles to the support site.
The Adjacency List is a somewhat inconvenient solution for organizing comments, since there can be problems with finding parent objects and building a tree structure, although the approach itself allows you to quickly remove and add elements.
Nested Set is a rather cumbersome method for organizing comments on a small site, and even if you look in the direction of large resources, then under articles there are not so often 5000 comments. I was also embarrassed by the fact that it would be necessary to add a hidden root element, the so-called first empty comment in the article, from which the whole tree will be built. Why produce extra entities? - Although maybe I'm wrong. Well, the last argument against was the need to recalculate keys when adding new comments. In general, despite the advantages of this structure, within the framework of this site and its current state - this way of storing comments will become gunfire on sparrows.
Materialized Path - Each comment contains the full path. And at the same time under the article can be organized several comment trees. That is, any comment that is on the first level is automatically considered root for its tree. And when you add a new comment, you must take the full path from the future parent and add to it only the ID of the new comment. when selecting comment trees, you can sort by these arrays, which automatically allows you to place all comments in chronological order while preserving the tree structure
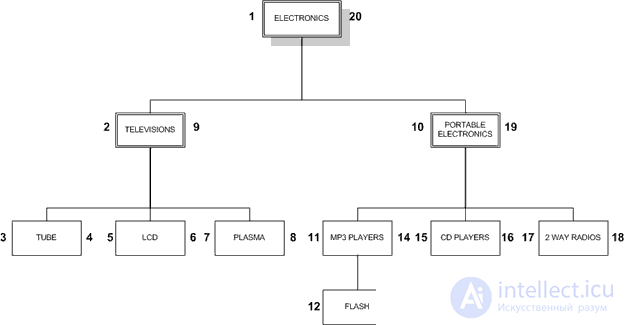
In our example, hierarchical data is a set of elements in which each element has one parent and zero or more children (except for the root element, which has no parents). Hierarchical data can be found in a variety of database applications, including forums and newsletters, business organization diagrams, content category management, and product categories. For our example, we will use the following hierarchy of product categories from a fictional electronics store:
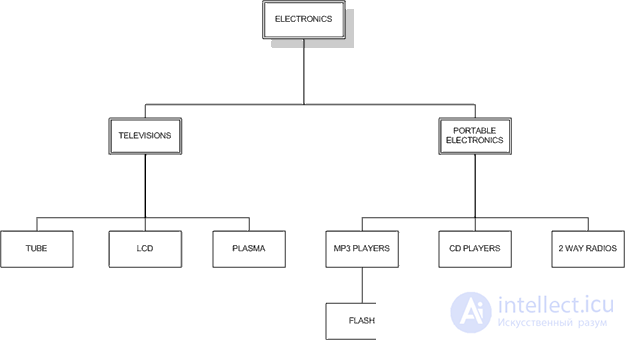
Mysql to version 8.0, it is possible to store hierarchical data in the form of nested walrus, model of the list of neighbors. Starting with version 8.0 of MYSQL, it is possible to work with table expressions to process and store hierarchical data.
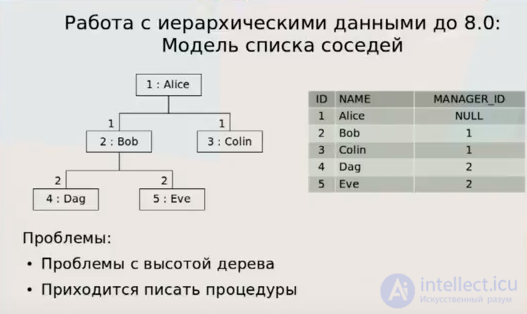


These categories form a hierarchy, like the examples above. In this article, we will look at two models for working with hierarchical data in MySQL, starting with the traditional Adjacency List Model.
Adjacency List Model
As a rule, the examples mentioned above will be stored in a table with the following definition (I include in the example all the CREATE and INSERT expressions so that we can follow along the train of thought):
(7, 'MP3 PLAYERS', 6), (8, 'FLASH', 7),
+ ------------- + ---------------------- + -------- +
| 3 | TUBE | 2 |
| 8 | FLASH | 7 |
In the adjacency list model, each element of the table contains a pointer to its parent. The topmost element, in this case ELECTRONICS , is NULL for its parents. Model adjacency has the advantage, you can quite easily see that FLASH is a child of MP3 PLAYERS , which is a child of portable electronics, which is a child of electronics. While the adjacency list model is fairly easy to implement, there may be a problem with SQL implementations.
Getting a full tree
The first common task when working with hierarchical data is to display the entire tree, as a rule, with different depths. The most common way to do this is in pure SQL , by combining tables:
LEFT JOIN category AS t4 ON t4.parent = t3.category_id
| ELECTRONICS | TELEVISIONS | TUBE | NULL |
| ELECTRONICS | PORTABLE ELECTRONICS | 2 WAY RADIOS | NULL |
View all leaf nodes
We can find all the nodes in the tree (i.e. without children) using
WHERE t2.category_id IS NULL ;
+ -------------- +
| CD PLAYERS |
Getting one way
Combining also allows us to see the full path of our hierarchy:
LEFT JOIN category AS t4 ON t4.parent = t3.category_id
| ELECTRONICS | PORTABLE ELECTRONICS | MP3 PLAYERS | FLASH |
The main limitation of this approach is that you need to combine for each level in the hierarchy, and the performance will deteriorate significantly with each added level, the complexity will increase.
Limitations of the Approximate Adjacency List
Working with a model adjacency list in pure SQL can be difficult at best. Before you see the full path to the category, we need to know at what level it is located. In addition, special attention should be paid to the removal of nodes due to the possibility of orphaning the entire branch (remove the category of portable electronics category and all its orphans). Some of these limitations can be resolved using client code or stored procedures. With procedural language, we can start at the bottom of the tree and repeat upwards the return of a full tree or one path. We can also use procedural programming to remove the nodes of an entire branch without orphanhood, promoting one child and changing the order of the rest of the children to point to the new parent.
Extended list of ridiculousness (sessions) in databases
sometimes add special fields of the level path in which to contain information about the node and the path to the parents
another kind of storage of the list of neighbors using the binary Materialized Path
Solving the problem of sorting trees using a binary Materialized Path
use not decimal IDs in the path, but encode to another number system in order to have less restrictions
in the length of the path. At the same time, separators in the form of dots or other characters are not needed, since the field will be
used only for sorting.
You can use the base 95, this is just the number of printable characters in ASCII.
If for each value in the path we use a fixed length, we get the following upper threshold ID:
1 - 95 ^ 1 - 1 = 94
2 - 95 ^ 2 - 1 = 9,024
3 - 95 ^ 3 - 1 = 857 374
4 - 95 ^ 4 - 1 = 81 450 624
5 - 95 ^ 5 - 1 = 7 737 809 374
5 characters is enough to not worry about the maximum number of comments.
The maximum level of nesting, in this case, for VARCHAR 255/5 = 51
Theoretically, it is possible to take not BASE95, but BASE256 (together with non-printing characters),
but storing it all is binary in a blob, although I’m not sure about performance with
sorting (need to check). Then by 3 characters we could encode
16,777,215 options, and 4–4,294,967,295.
/ * sorting nested comments along the way * /
function bpath ($ mpath, $ sep = '/', $ max_len = 5) {
$ bpath = ";
$ chunks = explode ($ sep, trim ($ mpath, $ sep));
$ zero = substr (BASE95, 0, 1);
foreach ($ chunks as $ chunk)
$ bpath. = str_pad ($ this-> dec2base ($ chunk, 95, $ BASE95), $ max_len, $ zero, STR_PAD_LEFT);
return $ bpath;
}
// convert a base value
function dec2base ($ dec, $ base, $ digits = FALSE) {
if ($ base <2 or $ base> 256) return error ("Invalid Base:". $ base, 0);
bcscale (0);
$ value = "";
if (! $ digits) $ digits = digits ($ base);
while ($ dec> $ base-1) {
$ rest = bcmod ($ dec, $ base);
$ dec = bcdiv ($ dec, $ base);
$ value = $ digits [$ rest]. $ value;
}
$ value = $ digits [intval ($ dec)]. $ value;
return (string) $ value;
}
$ BASE95 = '! "# $% & \' () * +, -. / 0123456789:; <=>? @ ABCDEFGHIJKLMNOPQRSTUVWXYZ [\] ^ _` abcdefghijklmnopqrstuvwxyz {|} ~ ';
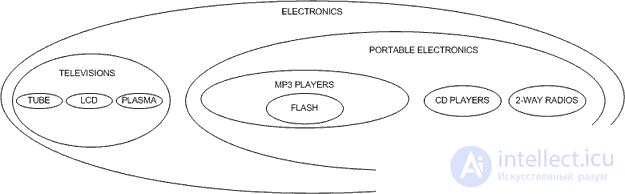
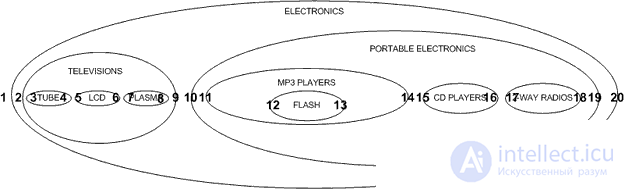
What I would like to dwell on in this article is a different approach, called, as a rule, the Nested Set Model . In the nested set model, we can look at our hierarchy in a new way, not as nodes and lines, but as nested containers. Let's try to draw our electronics categories as follows:
Please note that our hierarchy is still preserved; parent categories retain children. We represent this form of hierarchy in a table using pointers to the left and right nodes in our sets:
rgt INT NOT NULL
VALUES (1, 'ELECTRONICS', 1,20), (2, 'TELEVISIONS', 2,9), (3, 'TUBE', 3,4),
| category_id | name | lft | rgt |
| 4 | LCD | 5 | 6 |
| 9 | CD PLAYERS | 15 | 16 |
We use lft and rgt because left and right are MySQL reserved words; see http://dev.mysql.com/doc/mysql/en/reserved-words.html for a full list of reserved words.
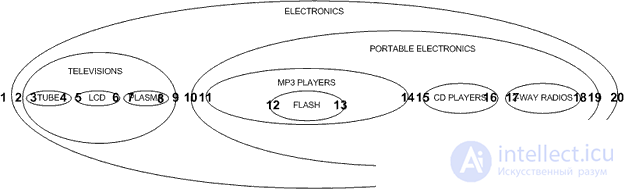
So how do we define left and right values? We start numbering on the left side of the external nodes and continue to the right:
This design can be represented by a typical tree, as in the image:
When working with a tree, we work from left to right, one layer after another, going down to the children of each node before assigning rgt and moving to the right. Such an approach is called a change in the tree traversal algorithm (preorder tree traversal algorithm).
Getting a full tree
We can get a complete tree using a join that binds parents to nodes on the basis that the lft value of the node will always appear between its parent's lft and the rgt value:
AND parent.name = 'ELECTRONICS'
| name |
| LCD |
| CD PLAYERS |
Unlike our previous model with the adjacency list model, this query will work regardless of the tree depth. We do not deal with the value of the rgt node in our predicate BETWEEN , since the value of rgt always falls under the same parents as the lft values.
Finding all end nodes
Finding all the nodes in the nested set model is even simpler than the LEFT JOIN method used in the adjacency list model. If you look at the nested_category table, you may notice that the LFT and RGT values for the end nodes are consecutive numbers. To find the end nodes, we look for nodes where rgt = lft + 1 :
| LCD |
+ -------------- +
Getting one way
With the model of nested sets, we can get one path without forming several table joins:
AND node.name = 'FLASH'
+ ---------------------- +
+ ---------------------- +
Determination of knot depth
We have already looked at how the entire tree is shown, but what if we also want to show the depth of each node in the tree to better determine how each node is placed in the hierarchy? This can be done by adding the COUNT function and the predicate (clause) GROUP BY to our existing queries to display the entire tree:
GROUP BY node.name
+ ---------------------- + ------- +
| PLASMA | 2 |
| 2 WAY RADIOS | 2 |
We can use the depth value to indent with our categories using the CONCAT and REPEAT string functions.
GROUP BY node.name
+ ----------------------- +
| PLASMA |
| 2 WAY RADIOS |
Of course, in the client application, you will often use the depth value directly to display the hierarchy. Web developers can repeat the loop on the tree by adding tags
and
as the size of the depth increases and decreases.
Subtree depth (branches)
When we need detailed information about a branch, we cannot limit the node or parent tables in our union (self-join), because it will spoil our results. Instead, we will add a third join, as well as a subquery, to determine the depth that will be the new starting point for our branch:
(
AND node.name = 'PORTABLE ELECTRONICS'
AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
| MP3 PLAYERS | 1 |
This function can be used with any node name, including the root node. The depth values are always relative to the node name.
Finding immediate subordinate nodes
Imagine that you are showing the categories of electronics products on the seller’s website. When a user clicks on a category, you want the products of this category to be displayed, and also its subcategories are listed immediately, but not the entire category tree under it. To do this, we need to show the nodes and its immediate subnodes, but not lower down the tree. For example, when showing the category PORTABLE ELECTRONICS , we want to show MP3 PLAYERS , CD PLAYERS and 2 WAY RADIOS , but not FLASH .
This can be easily done by adding a HAVING clause to our previous queries:
(
AND node.name = 'PORTABLE ELECTRONICS'
AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
| MP3 PLAYERS | 1 |
If you do not want the parent node to be displayed, change the HAVING depth <= 1 to HAVING depth = 1 .
Aggregation functions in nested sets
Let's add a table of products that we can use to demonstrate the aggregate functions:
);
('Power-MP3 5gb',7),('Super-Player 1gb',8),('Porta CD',9),('CD To go!',9),
+------------+-------------------+-------------+
| 3 | Super-LCD 42" | 4 |
| 8 | Porta CD | 9 |
Теперь давайте выполним запрос, который сможет получить дерево наших категорий, а также количество продуктов по каждой категории:
WHERE node.lft BETWEEN parent.lft AND parent.rgt
| TELEVISIONS | 5 |
| MP3 PLAYERS | 2 |
Это наше типичное целое дерево запроса с добавленными COUNT и GROUP BY , наряду со ссылкой на продукт таблицы и соединением между узлом и продуктами таблицы в предикате WHERE . Как вы видите, есть запись для каждой категории и число подкатегорий содержащихся в родительских категориях.
Добавление новых узлов
Теперь, когда мы узнали, как получить наше дерево, мы должны взглянуть на то, как обновить наше дерево путем добавления новых узлов. Давайте посмотрим на нашу схему модели вложенных множеств снова:
Если мы хотим добавить новый узел между узлами TELEVISIONS и PORTABLE ELECTRONICS , новый узел будет иметь lft и rgt значения 10 и 11, и все его узлы справа будут иметь свои lft и rgt значения увеличена на два. Затем мы добавляем новый узел с соответствующим значениями lft и rgt . Хотя это может быть сделано с помощью хранимых процедур в MySQL 5 , я буду считать, что в данный момент большинство читателей используют 4.1, так как это последняя стабильная версия, и я буду изолировать мой запрос с выражением LOCK TABLES :
WHERE name = 'TELEVISIONS';
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myRight;
Мы можем проверить наши вложения с нашими отступом дерева запроса:
GROUP BY node.name
| name |
| LCD |
| FLASH |
Если вместо этого мы хотим добавить узел в качестве дочернего узла, который не имеет существующих детей, мы должны немного изменить наши процедуры. Давайте добавим новый узел FRS ниже узла 2 WAY RADIOS :
WHERE name = '2 WAY RADIOS';
INSERT INTO nested_category(name, lft, rgt) VALUES('FRS', @myLeft + 1, @myLeft + 2);
Как видите, наш новый узел теперь правильно вложен:
GROUP BY node.name
| name |
| LCD |
| FLASH |
Удаление узлов
Последние основной задачей в работе с вложенными множествами заключается в удалении узлов. Набор ваших действий при удалении узла, зависит от положения узла в иерархии, удаление сделать листьев легче, чем удаление узлов с детьми, потому что мы должны обращаться с сиротами узлов.
При удалении листа узла, в отличие от добавления новых узлов, мы удаляем узел и его ширину от каждого узла правее:
FROM nested_category
UNLOCK TABLES;
И опять, мы выполняем запрос оформляя отступы в дереве, чтобы подтвердить что наш узел был удален без нарушения иерархии:
GROUP BY node.name
| name |
| LCD |
| CD PLAYERS |
Этот подход работает одинаково хорошо при удалении узла и всех его детей:
FROM nested_category
UNLOCK TABLES;
И опять, мы запрашиваем, чтобы увидеть, успешно ли мы удалили все ветки:
GROUP BY node.name
| name |
| LCD |
| FRS |
Другой сценарий, который можно использовать при удаление родительского узла, а не детей. В некоторых случаях вы можете просто изменить название заполнителя до замены представлены, например, когда увольняют руководителя. В других случаях, дочерние узлы должны быть подняты до уровня удаленного родителя:
FROM nested_category
В этом случае мы вычитаем два от всех элементов справа от узла (так как без детей, это будет иметь ширину двух), и один из узлов, которые являются его дети (чтобы закрыть пробел, созданный потерей левой родителей значение). Еще раз, мы можем подтвердить наши элементы были повышены:
GROUP BY node.name
| name |
| LCD |
+---------------+
Другие сценарии при удалении узлов будут включать содействие одному из детей родители положение и перемещение ребенка узлов под братом родительский узел, но ради пространство этих сценариев не рассматривается в этой статье.
Заключительное слово
Хотя я надеюсь, что информация в данной статье, будет полезна для вас, концепция вложенных множеств в SQL была вокруг в течение более десяти лет, и есть много дополнительной информации, имеющейся в книгах и в интернете. На мой взгляд, наиболее полным источником информации об управлении иерархической информации является книга под названием Деревья Джо Celko и иерархии в SQL для Smarties, написанная очень уважаемым автором в области передовых SQL, Джо Celko. Джо Celko часто приписывают модель вложенных множеств и на сегодняшний день является самым плодовитым автором по этому вопросу. Я нашел книгу Celkoto be an invaluable resource in your research and highly recommend it. The book discusses complex issues that I am not in this article, and also provides additional methods for managing hierarchical data in addition to the adjacency list and nested Set models.
Comments
To leave a comment
Databases - MySql (Maria DB)
Terms: Databases - MySql (Maria DB)