Lecture
Rectangle Formulas
Trapezoid formula
Simpson Formula
Problem Statement: It is required to find the value of a certain integral 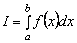 for some function f ( x ) defined on the segment [ a , b ]. For some functions, the value of the integral can be found exactly. However, in the general case, the value of the integral can only be found approximately using one or another method of numerical integration.
for some function f ( x ) defined on the segment [ a , b ]. For some functions, the value of the integral can be found exactly. However, in the general case, the value of the integral can only be found approximately using one or another method of numerical integration.
Numerical integration is based on replacing the integral by the sum of the form 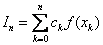 . Such a replacement follows from the definition of the integral as the limit of the sum
. Such a replacement follows from the definition of the integral as the limit of the sum 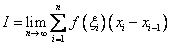 . Fixing n, we get the previous amount.
. Fixing n, we get the previous amount.
Approximate equality 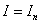 called the quadrature formula
called the quadrature formula 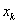 - quadrature nodes,
- quadrature nodes, 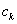 - coefficients of the quadrature formula . Difference
- coefficients of the quadrature formula . Difference 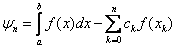 is called the quadrature error .
is called the quadrature error .
We divide the segment [a, b] into n parts, dots 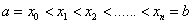 . And we will consider a uniform grid, i.e.
. And we will consider a uniform grid, i.e. 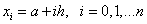 . Then
. Then 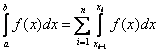 .
.
To construct a quadrature formula on the entire segment [a, b], it suffices to construct a quadrature formula on a partial segment 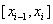 .
.
Let be 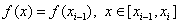 i.e. we approximate f (x) with left piecewise linear interpolation. Then we get
i.e. we approximate f (x) with left piecewise linear interpolation. Then we get 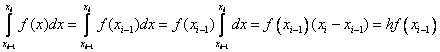 .
.
In this way, 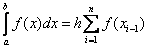 . This formula is called the left rectangle formula .
. This formula is called the left rectangle formula .
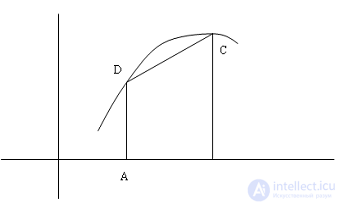
Geometric interpretation:

Given that the integral of some function gives the value of the area, then the area of the curvilinear region is replaced by the sum of the areas of the rectangles.
The formula for the right-hand rectangles is obtained in the same way. Here 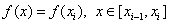 . As a result, we get:
. As a result, we get: 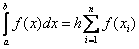

We estimate the error formulas. For example, the error formula of the left rectangles.
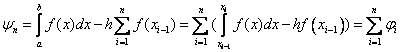 .
.

We use the Taylor formula:
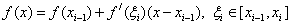
Then 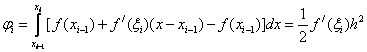
Let be 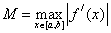 then
then 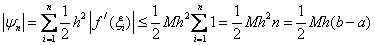 ,those. the formula of the left rectangles has the first in h order of accuracy .
,those. the formula of the left rectangles has the first in h order of accuracy .
Similarly, for the formula of right rectangles.
Formula of average rectangles . Here is the function on the segment 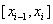 is replaced by its value in the middle of the segment, i.e.
is replaced by its value in the middle of the segment, i.e. 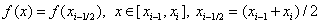
Then, we get 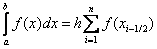 - This is the formula of medium rectangles.
- This is the formula of medium rectangles.
It is convenient to write it in the form 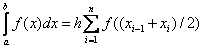
Let us estimate the error of the formula for average rectangles.
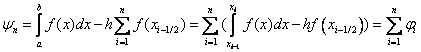
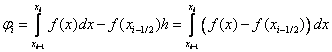
We use the Taylor formula:
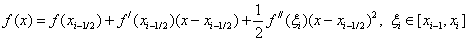

Let be  then
then
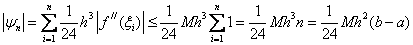 i.e. the formula of average rectangles has the second order of h accuracy
i.e. the formula of average rectangles has the second order of h accuracy
In all considered formulas, the area of the curvilinear trapezium was replaced by the area of the rectangles.
In this formula 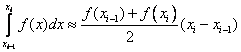 i.e. the area of the curved trapezoid, is replaced by the area of the rectangular trapezoid.
i.e. the area of the curved trapezoid, is replaced by the area of the rectangular trapezoid.
The trapezoid formula is obtained by replacing the integrand with an interpolation polynomial of the first degree:
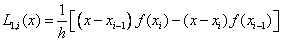 .
.
Really
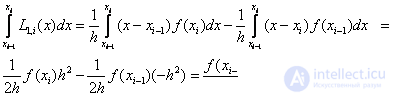
Then for the whole segment [a, b] we get:

 It can be shown that the trapezoid formula has the second order of accuracy .
It can be shown that the trapezoid formula has the second order of accuracy .
The trapezoid formula can be written as:
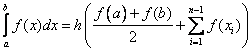
When approximating the integral 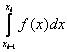 , function f (x) on a segment
, function f (x) on a segment 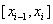 replace the parabola passing through the points
replace the parabola passing through the points 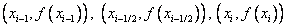 where
where 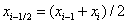 i.e. use for approximation of the second degree Lagrange polynomial:
i.e. use for approximation of the second degree Lagrange polynomial:
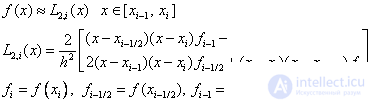

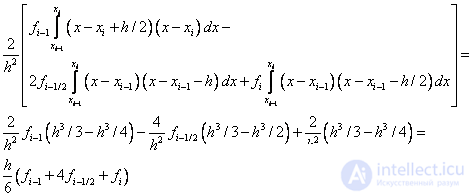
Therefore, we obtain the simpson formula
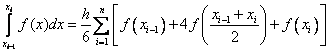
It can be shown that the Simpson formula has a fourth order of accuracy .
An example . Calculate the integral 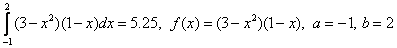 . We divide the segment [-1,2] into 10 parts, i.e.
. We divide the segment [-1,2] into 10 parts, i.e. 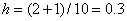 . We calculate the value of the integral by the formulas of the left, right, middle rectangles, by the trapezoid formula and the Simpson formula. To do this, make the table:
. We calculate the value of the integral by the formulas of the left, right, middle rectangles, by the trapezoid formula and the Simpson formula. To do this, make the table:
x i | f (x i ) | (x i-1 + x i ) / 2 | f ((x i-1 + x i ) / 2) | |
-one | four | -0.85 | 4.213375 | |
-0.7 | 4.267 | -0.55 | 4.181125 | |
-0.4 | 3.976 | -0.25 | 3.671875 | |
-0.1 | 3.289 | 0.05 | 2.847625 | |
0.2 | 2.368 | 0.35 | 1.870375 | |
0.5 | 1.375 | 0.65 | 0.902125 | |
0.8 | 0.472 | 0.95 | 0.104875 | |
1.1 | -0.179 | 1.25 | -0.359375 | |
1.4 | -0.416 | 1.55 | -0.328625 | |
1.7 | -0.077 | 1.85 | 0.359125 | |
2 | one | |||
S1 = | 19.075 | S3 = | 17.4625 | |
S2 = | 16.075 |
Here 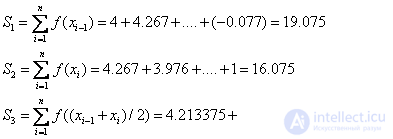
The formula of the left rectangles:
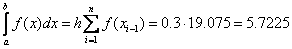
Formula of the right rectangles:
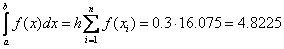
Formula of average rectangles:
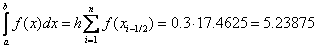
Formula trapezoid:
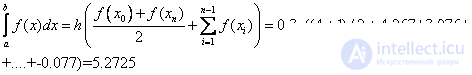
Simpson's formula:
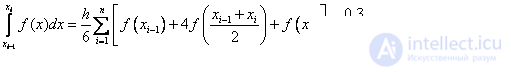
Recall that the exact value of the integral is 5.25
Comments
To leave a comment
Numerical methods
Terms: Numerical methods