Lecture
The method of dividing the segment in half (dichotomy)
Simple iteration method
Newton's method (tangent method)
Chord method
Formulation of the problem
Given a nonlinear algebraic equation
f ( x ) = 0 (1)
The nonlinearity of the equation means that the graph of the function is not a straight line, i.e. f (x) includes x to some extent or under the sign of the function.
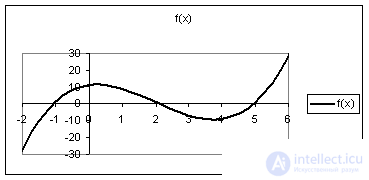
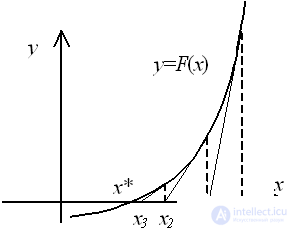
Solving the equation is finding x * ∈ R : f ( x * ) = 0. X * value called the root of the equation . A nonlinear equation can have several roots. The geometric interpretation of the roots of the equation is shown in Fig. 1. The roots of equation (1) are the points x 1 *, x 2 *, x 3 *, at which the function f ( x ) intersects the x axis.
 Methods for solving a nonlinear equation (1) can be divided into exact (analytical) and approximate (iterative). In exact methods, the root is represented by some algebraic formula. For example, solving quadratic equations, some trigonometric equations, etc.
Methods for solving a nonlinear equation (1) can be divided into exact (analytical) and approximate (iterative). In exact methods, the root is represented by some algebraic formula. For example, solving quadratic equations, some trigonometric equations, etc.
In approximate methods, the process of finding a solution is, generally speaking, infinite. The solution is obtained as an infinite sequence { x n }, such that 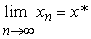 . By the definition of the limit, for any (arbitrarily small) ε , there exists N such that for n> N , | x n - x * | < ε . The members of this sequence x n are called successive approximations to the solution, or iterations. Forward, the given number ε is called the accuracy of the method, and N is the number of iterations that must be performed to obtain a solution with accuracy ε .
. By the definition of the limit, for any (arbitrarily small) ε , there exists N such that for n> N , | x n - x * | < ε . The members of this sequence x n are called successive approximations to the solution, or iterations. Forward, the given number ε is called the accuracy of the method, and N is the number of iterations that must be performed to obtain a solution with accuracy ε .
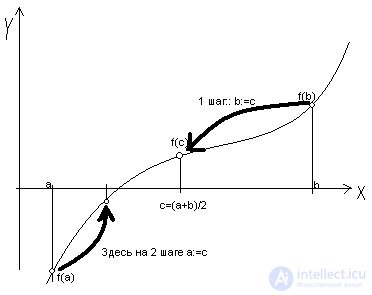
There are various methods for finding an approximate solution, i.e. methods for constructing a sequence of iterations { x n }, but all of them have common steps shown in the figure.

The following criterion for stopping an iterative process is most often used: | x n + 1 - x n | < ε , i.e. the difference between adjacent iterations becomes small. Also for the end of the iterative process the condition | f ( x n ) | < ε where f ( x n ) - method discrepancy .
Before using the approximate method, the equation must be investigated for the presence of roots and clarified where these roots are located, i.e. find root isolation intervals . The root isolation interval is the segment on which the root of the equation exists and is unique.
The necessary condition for the existence of the root of the equation on the interval [a, b]: Let f ( x ) be continuous and f ( a ) f ( b ) <0 (that is, the function has different signs at the ends of the interval). Then inside the segment [ a, b ] there exists at least one root of the equation f ( x ) = 0.
Sufficient condition of uniqueness of the root on the segment [a, b]:
The root will be unique if f ( a ) f ( b ) <0 and f / ( x ) does not change sign on the segment [ a, b ] , i.e. f ( x ) is a monotone function, in this case the segment [a, b] will be an isolation interval.
If there are several roots, then for each you need to find the isolation interval.
There are various ways to research a function: analytical, tabular, graphical .
The analytical method consists in finding the extrema of the function f ( x ), the study of its behavior in  and finding areas of increasing and decreasing function.
and finding areas of increasing and decreasing function.
The graphical method is plotting the function f ( x ) and determining the number of roots by the number of intersections of the graph with the x axis.
The tabular method is the construction of a table consisting of a column of argument x and a column of values of the function f ( x ) . The presence of roots is indicated by changes in the sign of the function. To avoid the loss of roots, the step of changing the argument must be small enough, and the interval of change is wide enough.
Example.
Solve the equation x 3 - 6x 2 + 3x + 11 = 0, i.e. f (x) = x 3 - 6x 2 + 3x + 11.
Find the derivative f / (x) = 3x 2 -12x + 3.
Find the zeros of the derivative f / (x) = 3x 2 -12x + 3 = 0; D = 144-4 * 3 * 3 = 108;
X 1 = 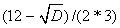 = 0.268;
= 0.268;
X 2 = 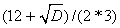 = 3.732;
= 3.732;
Since f / ( 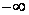 )> 0, then f / (x)> 0 with
)> 0, then f / (x)> 0 with 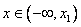 , f / (x) <0 with
, f / (x) <0 with 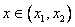 and f / (x)> 0 for
and f / (x)> 0 for 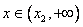 . In addition, f (
. In addition, f ( 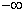 ) =
) = 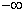 <0, f (
<0, f ( 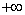 ) =
) = 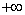 > 0 Therefore, on the interval
> 0 Therefore, on the interval 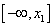 increases from
increases from 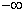 up to f (x 1 ) = 3x 1 2 -12x 1 + 3 = 11.39; on the interval
up to f (x 1 ) = 3x 1 2 -12x 1 + 3 = 11.39; on the interval 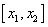 - decreases to f (x 2 ) = 3x 2 2 -12x 2 + 3 = -9.39 and on the interval
- decreases to f (x 2 ) = 3x 2 2 -12x 2 + 3 = -9.39 and on the interval 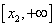 increases to
increases to 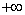 i.e. The equation has three roots.
i.e. The equation has three roots.
Find the isolation intervals for each of the roots.
Consider the segment [-2, -1] for the first root:
f (-2) = -27 <0, f (-1) = 1> 0, f / (x)> 0 with 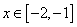 those. this segment is the root isolation interval.
those. this segment is the root isolation interval.
Consider the segment [1, 3] for the second root:
f (1) = 9> 0, f (3) = -7 <0, f / (x) <0 with 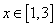 those. this segment is the root isolation interval.
those. this segment is the root isolation interval.
Consider the segment for the third root [4, 5]:
f (4) = -9 <0, f (5) = 1> 0, f / (x)> 0 with 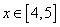 those. this segment is the root isolation interval.
those. this segment is the root isolation interval.
Tabular method:
x | -3 | -2 | -one | 0 | one | 2 | 3 | four | five | 6 | 7 |
f (x) | -79 | -27 | one | eleven | 9 | one | -7 | -9 | one | 29 | 81 |
Graphic way
Approximate (Iterative) methods.
Let the root isolation intervals be known. We will get acquainted with several iterative methods that allow finding the root on a known isolation interval [ a, b ] .
The idea of the method:
Find the midpoint of the segment [ a, b ]: c = ( a + b ) / 2 . The root remained on one of the parts: [ a, c ] or [ c, b ]. If f ( a ) * f ( c ) <0 , then the root fell on the segment [ a, c ], then the division of the segment can be repeated, taking the point c as the new right end, i.e. b = c . Otherwise, the root fell to half [ c, b ], and the value of the left end of the segment must be changed: a = c . Since the root is always enclosed within a segment, the iterative process can be stopped if the length of the segment becomes less than the specified accuracy: | b - a | < ε Find the first root of the equation f (x) = x 3 - 6x 2 + 3x + 11 = 0 with accuracy 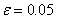
Calculations are made in the form of a table.
k | a | b | c | f (a) | f (c) | | ba | |
0 | -2 | -one | -1.5 | -27 | -10.375 | one |
one | -1.5 | -one | -1.25 | -10.375 | -4.07813 | 0.5 |
2 | -1.25 | -one | -1.125 | -4.07813 | -1.39258 | 0.25 |
3 | -1.125 | -one | -1.0625 | -1.39258 | -0.1604 | 0.125 |
four | -1.0625 | -one | -1.03125 | -0.1604 | 0.42868 | 0.0625 |
five | -1.0625 | -1.03125 | -1.04688 | -0.1604 | 0.136372 | 0.03125 |
6 | .......... | |||||
7 | ||||||
eight | ||||||
9 | ||||||
ten | -1.05469 | -1.05371 | -1.0542 | -0.01146 | -0.00218 | 0.000977 |
where a 0 b 0 - the initial boundaries of the interval of isolation of the root; 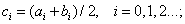
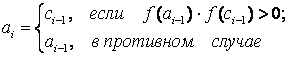
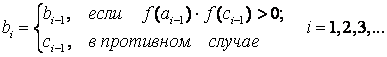
As a result of the calculation, the approximate value of the first root: 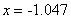 with accuracy
with accuracy 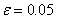 and x = -1.0542 with accuracy
and x = -1.0542 with accuracy 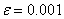 .
.
Graphic illustration of the method:
This example in Excel: dich.xls (20 Kb)
Using equivalent transformations, we bring the original equation f (x) to a form convenient for applying the simple iteration method: x = φ ( x ) . Choose the initial approximation x 0 ∈ [ a, b ] . The following iterations are found by the formula: x k +1 = φ ( x k ) , i.e. x 1 = φ ( x 0 ), x 2 = φ ( x 1 ), etc. The iterative process ends if | x k + 1 - x k | < ε . To present the original equation in the equivalent form x = φ ( x ) can be in an infinite number of ways. From all such representations choose the one that gives the sequence of calculations converging to the root. It's obvious that 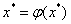 .
.
Sufficient condition for convergence: let φ ( x ) have a derivative on the segment [a, b], 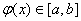 and
and 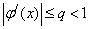 for all x from the segment [a, b], then the iterative process converges to the root of the equation ie
for all x from the segment [a, b], then the iterative process converges to the root of the equation ie 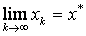 .
.
The proof follows from the following estimates:
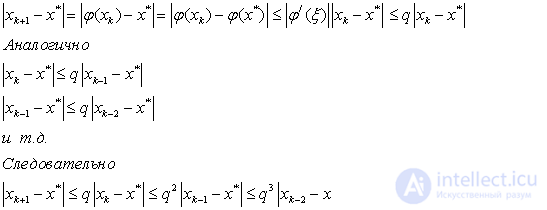
The first inequality follows from the Lagrange mean theorem and the fact that 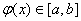 .
.
The rest of the inertia.
Because 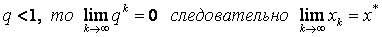 .
.
The geometric meaning of the method of simple iteration.
|
|
|
|
Convergent simple iteration method | |
| |
|
|
Divergent simple iteration method | |
The initial approximation is usually taken as the middle of the segment [a, b]: 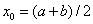 .
.
In practice, often as 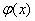 take function
take function 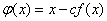 where c is some constant. The constant c is chosen so that
where c is some constant. The constant c is chosen so that 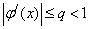 for all x ∈ [ a, b ] .
for all x ∈ [ a, b ] .
With this choice of function 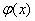 a simple iteration method is called a relaxation method.
a simple iteration method is called a relaxation method.
Get the conditions to choose from:
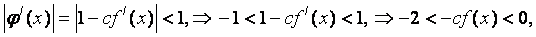
Thus, if f / ( x) <0, then 2 / f / ( x) < c <0. If f / ( x)> 0, then 2 / f / ( x)> c> 0.
It can be seen that the sign of y c coincides with the sign of f / (x). Often with take in the form of : 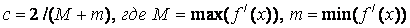 .
.
Make sure that such c satisfies the convergence condition:
Let f / (x)> 0. Then M> 0 and m> 0 -> c> 0 and 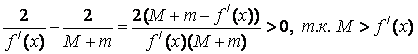 . Therefore, 2 / f / (x)> c> 0.
. Therefore, 2 / f / (x)> c> 0.
Let f / (x) <0. Then M <0 and m <0-> c <0 and
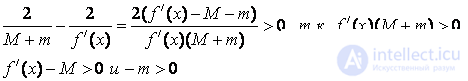
Therefore, 2 / f / (x) <c <0.
Find the second root of our original equation x 3 - 6x 2 + 3x + 11 = 0, which lies on the interval [1, 3] with accuracy 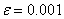 .
.
First we find the function 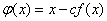 . In our case, f (x) = x 3 - 6x 2 + 3x + 11.
. In our case, f (x) = x 3 - 6x 2 + 3x + 11.
To find c, it is necessary to find the maximum and minimum values of f / (x) on the interval [1, 3]. To do this, it is necessary to find the values of f / (x) at the ends of the interval and at the points where f // (x) = 0, i.e. at the extremum points, if such points exist for the interval in question. And choose among these values f / (x) the maximum and minimum values.
f / (1) = 3x 2 -12x + 3 = -6, f / (3) = - 6, f // (x) = 6x-12 = 0 at x = 2  , f / (2) = - 8.
, f / (2) = - 8.
Consequently, 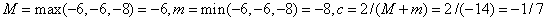
In this way, 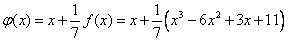 .
.
Calculations arrange in the form of a table:
k | x | | x k + 1 -x k | | | f (x k ) | |
0 | 2 | - | one |
one | 2.142857 | 0.142857 | 0.282799 |
2 | 2.102457 | 0.0404 | 0.07896 |
3 | 2.113737 | 0.01128 | 0.022164 |
four | 2.110571 | 0.003166 | 0.006213 |
five | 2.111459 | 0.000888 | 0.001742 |
6 | 2.11121 | 0.000249 | 0.000489 |
Here x 0 = (1 + 3) / 2 = 2, 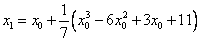 ,
, 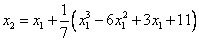 etc.
etc.
The condition for the end of the iterative process is the condition: | x k + 1 - x k | < ε or | f ( x k ) | < ε .
Recall that we solve the equation f (x) = 0.
The method is determined by the formula

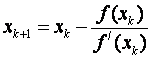
The geometric interpretation is as follows: a portion of the curve y = f (x) with 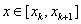 , if a
, if a 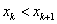 , or
, or 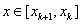 , if a
, if a 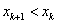 , is replaced by the segment of the tangent drawn from the point x k .
, is replaced by the segment of the tangent drawn from the point x k .
The tangent equation is 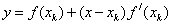 . Find the intersection point, which we denote by x k +1 , tangent to the axis y = 0:
. Find the intersection point, which we denote by x k +1 , tangent to the axis y = 0: 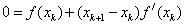 .
.
From where 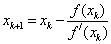 .
.
It can be shown that | x k + 1 - x * | < q * | x k - x * | 2 , i.e. The method converges with the second order.
Newton's method can be interpreted as a simple iteration method when 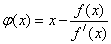 .
.
Remark . If the isolation interval of the root of the equation is known in which f // (x) does not change sign, then as the initial approximation one takes the end of the isolation interval for which the signs f (x) and f // (x) coincide.
Find the third root by Newton's method of our original equation x 3 - 6x 2 + 3x + 11 = 0, which lies on the interval [4, 5] with an accuracy of 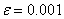 . First, make sure that f // (x) does not change the sign on this segment.
. First, make sure that f // (x) does not change the sign on this segment.
f // (x) = 6x-12. f // (x)> 0 for x> 2, i.e. f // (x)> 0 on the interval [4,5]. Since f (5) = 1> 0, then x 0 = 5.
Calculations arrange in the form of a table:
k | x k | | x k + 1 -x k | | f (x k ) | f / (x k ) |
0 | five | - | one | 18 |
one | 4.944444 | 0.055556 | 0.027606 | 17.00926 |
2 | 4.942821 | 0.001623 | 2.33E-05 | 16.98059 |
3 | 4.94282 | 1.37E-06 | 1.66E-11 | 16.98057 |
Here f (x k ) = x k 3 - 6x k 2 + 3x k +11, f / (x k ) = 3x k -12x k +3, 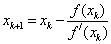 .
.
As root, you can take the value: x = 4.943. It is evident that the process came together already at the second iteration.
For comparison, we find the first root of our equation x 3 - 6x 2 + 3x + 11 = 0 on the interval [-2, -1] by the Newton method:
Since f // (x) = 6x-12, then f // (x) <0 on the interval [-2, -1], and since f (-2) = - 27> 0, x 0 = -2
k | x k | | x k + 1 -x k | | f (x k ) | f / (x k ) |
0 | -2 | -27 | 39 | |
one | -1.30769 | 0.692308 | -5.41966 | 23.82249 |
2 | -1.08019 | 0.227502 | -0.50182 | 19.46272 |
3 | -1.05441 | 0.025783 | -0.00613 | 18.9882 |
four | -1.05408 | 0.000323 | -9.5E-07 | 18.98229 |
five | -1.05408 | 5.02E-08 | -2.3E-14 | 18.98229 |
Recall that by the dichotomy method we reached the given accuracy of 0.001 at the 10th iteration.
We calculate the second root of our equation on the interval [1,3]. Note that f // (x) = 6x-12 changes its sign on the segment for x = 2. Reduce the isolation interval so that f // (x) does not change sign. Consider the interval [2.1; 3]. f // (2.1) = 6 * 2.1-12 = 0.6> 0 bf (2.1) = 0.101> 0. Therefore, x 0 = 2.1.
k | x k | | x k + 1 -x k | | f (x k ) | f / (x k ) |
0 | 2.1 | 0.101 | -8.97 | |
one | 2.11126 | 0.01126 | 3.95E-05 | -8.96286 |
2 | 2.111264 | 4.4E-06 | 6.47E-12 | -8.96286 |
3 | 2.111264 | 7.22E-13 | 0 | -8.96286 |
If we compare it with a simple iteration method, then we get the value of this root in two iterations instead of six.
These examples show that Newton's method is more rapidly converging. But to use it, it is necessary to take an initial approximation close enough to the root.
Simplified Newton's method . This modification of the Newton method is used if the derivative f / ( x ) is a complex function, and a lot of time is used to calculate it at each iteration. Let x 0 be the initial approximation and calculate the derivative z = f / ( x 0 ) . The following iterations use the calculated derivative value: 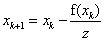 . This simplification somewhat slows down the process of convergence to a solution, but it reduces the time of each iteration cycle.
. This simplification somewhat slows down the process of convergence to a solution, but it reduces the time of each iteration cycle.
In this method, the curve f (x) is replaced by a straight line, a chord, of a tightening point (a, f (a)) and (b, f (b)). Depending on the sign of the expression f (a) f // (a), the chord method has two options, shown in fig. 2 a, b.
|
|
Fig. 2. Chord Method for F ( a ) F // ( a ) > 0 (a) and F ( a ) F // ( a ) < 0 ( b ) | |
Let f (a) f // (a)> 0 (Fig. 2 a). Then x 0 = b, the point a will remain fixed. The next approximation x 1 is found as the intersection point of the chord connecting the points (a, f (a)) and (x 0 , f (x 0 )) with the x axis. Chord equation: 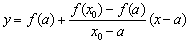 . Then the intersection point of the chord with the x axis:
. Then the intersection point of the chord with the x axis: 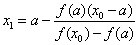 .
.
Now suppose that f (a) f // (a) <0 (Fig. 2). Then x 0 = a, point b is fixed. Let us draw a chord connecting the points (b, f (b)) and (x 0 , f (x 0 )): 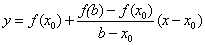 . Вычисляем точку пересечения хорды с осью x:
. Вычисляем точку пересечения хорды с осью x: 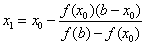 .
.
На следующей итерации в качестве x 0 надо взять вычисленное значение x 1 .
Таким образом, имеем следующую последовательность вычислений:
Если f(a) f // (a)>0, то x 0 =b и 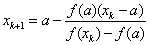 .
.
Если же f(a) f // (a)<0, то x 0 =a и 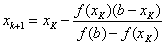 .
.
Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: | f ( x 1 )| < ε или 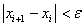 .
.
Задание. Найти первый и третий корень уравнения x 3 ‑ 6x 2 +3x+11=0 методом хорд.
Для первого корня a=-2, b=-1. 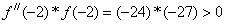 , тогда расчет ведется по первым формулам: x 0 =b и
, тогда расчет ведется по первым формулам: x 0 =b и 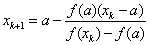 .
.
k | x k | |x k+1 -x k | | f(x k ) |
0 | -one | one | |
one | -1.03571 | 0.035714 | 0.345618 |
2 | -1.0479 | 0.012187 | 0.117007 |
3 | -1.05201 | 0.004108 | 0.039334 |
four | -1.05339 | 0.001379 | 0.013192 |
five | -1.05385 | 0.000462 | 0.004421 |
Для последнего корня: a=4, b=5, 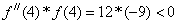 , тогда расчет ведется по вторым формулам: x 0 =a и
, тогда расчет ведется по вторым формулам: x 0 =a и 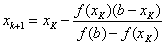 .
.
k | x k | |x k+1 -x k | | f(x k ) |
0 | four | -9 | |
one | 4.9 | 0.9 | -0.711 |
2 | 4.941555 | 0.041555 | -0.02147 |
3 | 4.942783 | 0.001229 | -0.00062 |
four | 4.942819 | 3.57E-05 | -1.8E-05 |
Comments
To leave a comment
Numerical methods
Terms: Numerical methods