Lecture
1. Obtain a solution to the equation f ( x) = x 3 + x 2 -9x + 9 = 0 by dividing the segment in half with an accuracy of 0.05. Isolation interval (-4, -3.8)
We verify that this segment is an isolation interval: f (-4) = - 3, f (-3.8) = 2.768.

Consequently,
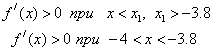
This segment is an isolation interval.
Calculations
|
k |
a |
b |
c |
f (c) |
f (a) |
ba |
|
0 |
-four |
-3.8 |
-3.9 |
-3 |
-0.009 |
0.2 |
|
one |
-3.9 |
-3.8 |
-3.85 |
-0.009 |
1.405875 |
0.1 |
|
2 |
-3.9 |
-3.85 |
-3.875 |
-0.009 |
0.705078 |
0.05 |
|
3 |
-3.9 |
-3.875 |
-3.8875 |
-0.009 |
0.349705 |
0.025 |
Calculation formulas:
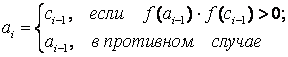
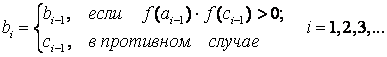
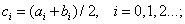
Answer: x = -3.8875
2. Obtain a solution to the equation f ( x) = x 3 + x 2 -9x + 9 = 0 using a simple iteration method with an accuracy of 0.001. Isolation interval (-5, -3).
Similarly, we prove that the interval is an isolation interval.
f (-5) = - 46, f (-3) = 18
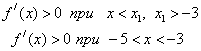
Calculation formulas:
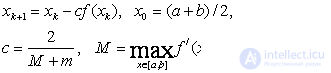
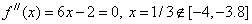
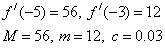
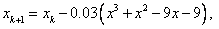
|
k |
x |
f (x) |
accuracy |
|
0 |
-four |
-3 |
|
|
one |
-3.91 |
-0.29837 |
0.09 |
|
2 |
-3.90105 |
-0.03925 |
0.008951 |
|
3 |
-3.89987 |
-0.00529 |
0.001178 |
|
four |
-3.89971 |
-0.00072 |
0.000159 |
Answer: X = -3.8997
3. Obtain a solution to the equation f ( x) = x 3 + x 2 -9x + 9 = 0 by the Newton method with an accuracy of 0.001. Isolation interval (-5, -3).
Calculation formulas:

f (-5) = -46, f // (-5) = 6 * (- 5) + 2 = -28
Consequently, 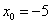
|
k |
x |
f (x) |
f '(x) |
accuracy |
|
0 |
-five |
-46 |
56 |
|
|
one |
-4.17857 |
-8.89217 |
35.02423 |
0.821429 |
|
2 |
-3.92469 |
-0.72721 |
29.36009 |
0.253886 |
|
3 |
-3.89992 |
-0.00659 |
28.82821 |
0.024769 |
|
four |
-3.89969 |
-5.6E-07 |
28.82332 |
0.000229 |
Answer: x = -3.89969
4. Solve a system of linear equations by simple iteration with an accuracy of 0.05:

Check the condition of diagonal dominance:

Solve the system of equations for x i

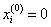
|
k |
x1 |
x2 |
x3 |
accuracy |
|
0 |
0 |
0 |
0 |
|
|
one |
-0.3333333 |
-0.125 |
-one |
one |
|
2 |
-0.0138889 |
-0.33333 |
-1.07639 |
0.319444 |
|
3 |
-0.0115741 |
-0.26302 |
-1.05787 |
0.070313 |
|
four |
-0.0099344 |
-0.26013 |
-1.04577 |
0.012105 |
5. Solve the system of linear equations by the Gauss – Seidel method with an accuracy of 0.05:

Similarly, we check the condition of diagonal dominance.
Solve the system of equations for x i

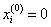
|
k |
x1 |
x2 |
x3 |
accuracy |
|
0 |
0 |
0 |
0 |
|
|
one |
-0.3333333 |
-0.20833 |
-1.09028 |
1.090278 |
|
2 |
0.0069444 |
-0.25955 |
-1.0421 |
0.340278 |
|
3 |
-0.0148052 |
-0.25896 |
-1.04563 |
0.02175 |
6. For the table given function:
| x | -2 | one | 1.5 | 2 |
| f | 0.1 | -0.2 | 0.5 | 1.2 |
calculate the value of the function at the point z = 1.2, using linear interpolation formulas.
We define the interval to which z belongs: [1,1.5].
Calculation formulas:
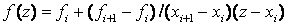
f (z) = - 0.2 + (0.5 + 0.2) / (1.5-1) * (1.2-1) = 0.2375.
7. For a table-specific function:
| x | -2 | one | 1.5 | 2 |
| f | 0.1 | -0.2 | 0.5 | 1.2 |
write the basic polynomials and calculate the value of the Lagrange polynomial at the point z = 1.2.
n = 3.

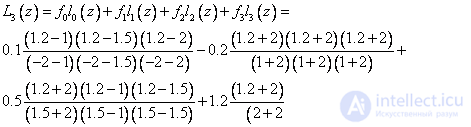
8. Calculate the integral by the trapezoid method for the function given in the table:
|
X |
-one |
-0.5 |
0 |
one |
|
f |
2 |
3 |
four |
4.5 |
In this task, x changes with a constant step of 0.5
Formula trapezoid:
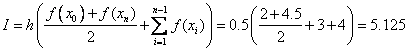
If the step is not constant, for example:
|
X |
-one |
-0.6 |
0 |
0.8 |
|
f |
2 |
3 |
four |
4.5 |
then it is necessary to use the general trapezium formula:

Similarly for left and right rectangle formulas:
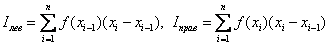
9. The method of least squares .
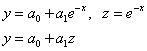
|
Z |
Z 1 |
Z 2 |
... |
Z n |
|
y |
Y 1 |
Y 2 |
... |
Y n |

Comments
To leave a comment
Numerical methods
Terms: Numerical methods