Lecture
Integer Type Operations
All operations that are performed on integers can be divided into the following groups.
Arithmetic operations
Arithmetic operations include:
Between dual pluses and minuses you can not leave spaces. Addition, subtraction and multiplication of integer values are performed as usual, but the division of integer values results in the whole again (the so-called "integer division"), for example, 5/2 will result in 2 , not 2.5 , but 5 / (- 3 ) will give -1 . The fractional part is simply discarded, the truncation of the particular occurs. This is initially discouraging, but then it turns out to be convenient for truncating numbers.
Comment
In Java, integer division is accepted.
This strange rule for mathematics is natural for programming: if both operands are of the same type, then the result is of the same type. It is enough to write 5 / 2.0 or 5.0 / 2 or 5.0 / 2.0 and we get 2.5 as the result of dividing real numbers.
The modulo division operation is defined as follows: a% b = a - (a / b) * b ; for example, 5% 2 will result in 1 , and 5% (-3) will give, 2 , because 5 = (-3) * (-1) + 2 , but (-5)% 3 will give -2 , because -5 = 3 * (-1) -2 .
The increment and decrement operations mean an increase or decrease in the value of a variable by one and apply only to variables, but not to constants or expressions, you cannot write 5 ++ or (a + b) ++ .
For example, after the above descriptions, i ++ will give -99 , a j-- will give 99 .
Interestingly, these operations' can be written? And before a variable: ++ i , - j . The difference will manifest itself only in the expressions: in the first record form (postfix) , the old value of the variable participates in the expression and only then its value increases or decreases. In the second form of the record (prefix) , the variable will first change and its new value will participate in the expression.
For example, after the above descriptions, (k ++) + 5 will result in 10004 , and the variable k will take the value 10,000 . But in the same initial situation (++ k) + 5 will give 10005 , and the variable k will become equal to 10000 .
Cast
The result of an arithmetic operation is of type int, except in the case when one of the operands of type long . In this case, the result will be a long type.
Before performing an arithmetic operation, there is always an increase (promotion) of the types byte , short , char . They are converted to type int , and maybe to type long , if another operand of type long . An operand of type int rises to type long if another operand is of type long . Of course, the numerical value of the operand does not change.
This rule sometimes leads to unexpected results. Attempting to compile a simple program, shown in Listing 1.3, will result in the compiler messages shown in Figure 2. 1.3.
Listing 1.3. Invalid variable definition
class InvalidDef {
public static void main (String [] args) {
byte b1 = 50, b2 = -99;
short k = b1 + b2; // Wrong! '
System.out.println ("k =" + k);
}
}
These messages mean that a possible loss of precision was found in the InvalidDef.java file, in line 4. Then the detected (found) and required (required) types are given, the string in which the error is detected (and not made) is displayed, and the symbol is marked, during the parsing of which an error was found. Then the total number of errors found (and not made) is indicated (1 error).
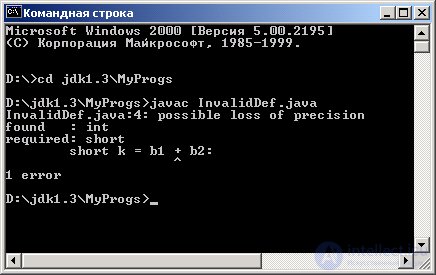
Fig. 1.3. Compiler error messages
In such cases, you must perform an explicit type conversion. In this case, it will be the narrowing of the int type to the short type. It is performed by an explicit cast operation, which is written in front of the rendered value as a type name in brackets. Definition
short k = (short) (b1 + b2) ;
will be true.
Narrowing is done simply by dropping the high-order bits, which must be taken into account for large values. For example, the definition
byte b = (byte) 300;
gives variable b the value 44 . Indeed, in the binary representation of the number 300 , equal to 100101100 , the most significant bit is discarded and it turns out 00101100 .
In the same way, it is possible to produce an explicit expansion (widening) of the type, if necessary. .
If the result of an entire operation is outside the range of its int or long type , then a modulo automatically equal to the length of this range occurs, and the calculations continue, no overflow occurs.
Comment
There is no integer overflow in Java.
Comparison operations
In Java, there are six common comparisons of integers by value:
Dual characters are written without spaces, they cannot be rearranged in places, the record => will be incorrect.
The result of the comparison is a logical value: true , as a result of, for example, a comparison of 3! = 5 ; or false , for example, by comparing 3 == 5 .
Logical operations should be used to record complex comparisons. For example, in calculations it is often necessary to do checks of the form a <x <b . Such an entry in the Java language will result in an error message, since the first comparison, and <x , will give true or false , and Java does not know if it is more than b , or less. In this case, you should write the expression (a <x) && (x <b) , and here the brackets can be omitted, just write a <x && x <b , but more on that later.
Bitwise operations
Sometimes you have to change the values of individual bits in whole data. This is done using bitwise operations by applying a mask. There are four bitwise operations in Java:
They are executed one by one, after both operands are reduced to the same type of int or long , as well as for arithmetic operations, and therefore to the same bit depth. Operations on each pair of bits are performed according to the table. 1.3.
Table 1.3. Bitwise operations
nl | n2 | ~ nl | nl & n2 | nl | n2 | nl ^ n2 |
one one 0 0 | one 0 one 0 | 0 0 one one | one 0 0 0 | one one one 0 | 0 one one 0 |
In our example, b1 == 50 , binary representation 00110010, b2 == -99 , binary representation 10011101 . Before the operation, it is raised to the int type. We get representations from 32 digits for b1 - 0 ... 00110010 , for b2 - 1 ... l0011101 . As a result of bitwise operations, we get:
The binary representation of each result takes 32 bits.
Note that the addition ~ x is always equivalent to (-x) -1 .
Shifts
There are three binary shift operations in Java:
These operations are peculiar in that the left and right operands in them have a different meaning. On the left is the value of the integer type, and the right side shows how many bits the value in the left side is shifted.
For example, the operation b1 << 2 will shift to the left by 2 digits a pre-increased value 0 ... 00110010 of the variable b1, which will result in 0 ... 011001000, decimal 200. The digits freed to the right will be filled with zeros, the left digits behind the 32nd bit lost.
Operation b2 << 2 will shift the increased value of 1 ... 10011101 by two digits to the left. As a result, we get 1 ... 1001110100, the decimal value is 396.
Note that a shift to the left by n digits is equivalent to multiplying a number by 2 to the power n.
Operation b1 >> 2 will result in 0 ... 00001100, decimal 12, and b2 >> 2 - the result is 1..11100111, decimal -25, i.e. the most significant bit to the left is distributed, the right bits are lost. This is the so-called arithmetic shift.
The operation of unsigned shift in all cases places zeroes on the left of the vacant positions, making a logical shift. But due to a preliminary increase, this has an effect only for a few high-order digits of negative numbers. So, b2 >>> 2 has the result 001 ... 100111, decimal number 1 073 741 799.
If we want to obtain a logical shift of the initial value of loomoi of the variable b2, i.e., 0 ... 00100111, we must first put a mask on b2 , zeroing the high-order bits: (b2 & 0XFF) >>> 2.
Comment
Be careful when using shifts to the right.
Real types
There are two real types in Java: float and double. They are characterized by a bit depth, a range of values, and a presentation accuracy that meets the IEEE 754-1985 standard with some modifications. Three more values are added to regular real numbers. ”
1. Positive infinity, expressed by the constant POSITIVE_INFINITY and arising from the overflow of a positive value, for example, as a result of the multiplication operation 3.0 * 6е307.
2. Negative infinity NEGATIVE_INFINITY .
3. "Not a number", written by the constant NaN (Not a Number) and arising from dividing a real number by zero or multiplying zero by infinity.
In chapter 4 we will talk about them in more detail.
In addition, the standard distinguishes between positive and negative zero, which occurs when the corresponding sign is divided by infinity, although comparison oo == oo gives true.
The operations with infinity are performed according to the usual mathematical rules.
In all other respects, real types are ordinary, real values, to which all arithmetic operations and comparisons listed for integer types are applicable. Characteristics of real types are given in table. 1.4.
Connoisseurs C / C ++
In Java, taking the remainder * of the division of%, increment ++ and decrement - also applies to real types.
Table 1.4. Real types
Type of | Digit | Range | Accuracy |
float | four | 3.4 e-38 <| x | <3.4 e38 | 7-8 digits |
double | eight | 1.7e-308 <| x | <1.7e308 | 17 digits |
Examples of the definition of real types:
float x = 0.001, y = -34.789;
double 21 = -16.2305, z2;
Since all arithmetic operations and comparisons are applicable to real types, whole and real values can be mixed in operations. In this case, the type conversion rule is supplemented with the following conditions:
Assignment operations
A simple assignment operator is written with an equal sign =, to the left of which there is a variable, and to the right an expression compatible with the type of variable: x = 3.5, y = 2 * (x - 0.567) / (x + 2), b = x <y, bb = x> = y && b.
The assignment operation works like this: the expression after the equal sign is calculated and reduced to the type of the variable to the left of the equal sign. The result of the operation will be the reduced value of the right side.
The assignment operation has another, side, action: the variable on the left receives the reduced value of the right side, its old value is lost.
In the assignment operation, the left and right parts are not equal, it is impossible to write 3.5 = x. After the operation x = y, the variable x will change, becoming equal to y, and after y = x, y will change.
In addition to the simple assignment operation, there are 11 more compound assignment operators: + =, - =, * =, / =,% =, & =, | =, ^ =, << =, >> = ; >>> =. Characters are written without spaces, you can not rearrange them in places.
All compound assignment operations operate according to the same scheme:
x or = a is equivalent to x = (type x), i.e. (x or a).
Recall that the ind variable of the short type is defined with the value 1. The assignment ind + = 7.8 will result in the number 8, and the variable ind will also receive the same value. This operation is equivalent to the simple assignment operation ind = (short) (ind + 7.8).
Before assignment, if necessary, the type is automatically cast. Therefore:
byte b = 1;
b = b + 10; // Mistake!
b + = 10; // Right!
Before addition + 50, an increase occurs to the type int, the result of the addition will also be of type int and, in the first case, cannot be Assigned to a variable b without explicit type conversion. In the second case, before assignment, the result of the addition will be narrowed to the type byte.
Conditional operation
This kind of operation has three operands. Initially, an arbitrary logical expression is written, that is, having true or false as a result, then a question mark, then two arbitrary expressions separated by a colon, for example,
x <0? 0: x
x> y? x - y: x + y
The conditional operation is performed as follows. First, a logical expression is evaluated. If true, then the first expression after the question mark is calculated? and its value will be the result of the whole operation. The last expression is not evaluated. If the result is false, then only the last expression is evaluated, its value will be the result of the operation.
This allows you to write n == o? yes: m / n without fear of division by zero. The conditional operation at first seems strange, but it is very convenient for recording small ramifications.
Expressions
Expressions are made up of constants and variables, operations on them, calls to methods and brackets. Of course, all elements of the expression must be compatible, it is impossible to write, for example, 2 + true. When calculating an expression, four rules are executed:
1. Operations of one priority are calculated from left to right: x + y + z is calculated as (x + y) + z. Exception: assignment operations are calculated from right to left: x = y = z is calculated as x = (y = z).
2. The left operand is calculated before the right operand.
3. Operands are fully evaluated before performing the operation.
4. Before performing the composite assignment operation, the value of the left part is saved for use in the right part.
The following examples show the features of the first three rules. Let be
int a = 3, b = 5;
Then the result of the expression b + (b = 3) is the number 8; but the result of the expression (b = 3) + b is the number 6. The expression b + = (b = 3) will result in 8, because it is calculated as the first of the above expressions.
Connoisseurs C / C ++
Most compilers of C ++ compute the value 8 in all these cases.
The fourth rule can be demonstrated as follows. Under the same definitions, a and b as a result of the calculation of the expression b + = a + = b + + = 7 we get 20. Although the assignment operations are performed from right to left and after the first, right, operation, the value of b becomes 12, but in the last, left assignment the old value of b is equal to 5. And as a result of two consecutive calculations, a + = b + = 7; b + = a; we get 27, because in the second expression a new value of the variable b is taken, equal to 12.
Connoisseurs C / C ++
Most C ++ compilers will calculate 27 in both cases.
Expressions can be complex and confusing. In such cases, the question arises about the priority of operations, which operations will be performed first. Naturally, multiplication and division are done before addition and subtraction. The remaining rules are listed in the next section.
The order of calculation of the expression can always be adjusted by brackets, they can be bent as much as necessary. But here it is important to observe the "middle ground". When a large number of brackets decreases the visibility of the expression and it is easy to err in the arrangement of brackets. If the expression with brackets is correct, then the compiler can track only the pair of brackets, but not the correctness of their placement.
Priority of operations
Operations are listed in decreasing order of priority. Operations on the same line have the same priority.
1. Postfix operators ++ and -.
2. Prefix operations ++ and -, addition ~ and negation!.
3. Type reduction (type).
4. Multiplication *, division / and taking the remainder%.
5. Addition + and subtraction -.
6. Shifts <<, >>, >>>.
7. Comparisons>, <,> =, <=.
8. Comparisons ==,! =.
9. Bitwise conjunction &.
10. Bitwise exclusive OR ^.
11. Bitwise disjunction | .
12. The conjunction &&.
13. Disjunction | | .
14. Conditional operation?:.
15. Assignments =, + =, - =, * =, / =,% =, & =, ^ =, | =, <<, >>, >>>.
Not all Java operations are listed here, the list will be updated as new operations are studied.
Connoisseurs C / C ++
In Java, there is no comma operation, but the list of expressions is used in the for loop operator.
Operators
As you know, any algorithm intended for execution on a computer can be developed using only linear calculations, branching and cycles.
You can write it in different forms: in the form of a flowchart, in pseudocode, in ordinary language, as we write down culinary recipes, or in some other “algorithms”. , -.
Every programming language must have a means of recording algorithms. They are called statements of the language. The minimum set of operations
The rator should contain an operator for recording linear calculations, a conditional operator for recording branching, and a loop operator.
Typically, the composition of programming language operators is wider: for the convenience of writing algorithms, several cycle operators, a variant operator, transition operators, object description operators are included in the language.
The Java language statement set includes:
This is not the entire set of Java operators, it will be supplemented as you learn the language.
Comment
There is no goto statement in Java.
Each statement is terminated by a semicolon.
You can put a semicolon at the end of any expression, and it will become an expression statement. But this makes sense only for assignment, increment and decrement operations and method calls. In other cases, it is useless, because the calculated value of the expression is lost.
Connoisseurs of Pascal
The semicolon in Java does not separate operators, but is part of an operator.
Linear execution of the algorithm is provided by sequential recording of operators. Переход со строки на строку в исходном тексте не имеет никакого значения для компилятора, он осуществляется только для наглядности и читаемости текста.
Блок
Блок заключает в себе нуль или несколько операторов с целью использовать их как один оператор в тех местах, где по правилам языка можно записать только один оператор. Например, {х = 5; у = ?;}. Можно записать и пустой блок, просто пару фигурных скобок {}.
Блоки операторов часто используются для ограничения области действия переменных и просто для улучшения читаемости текста программы.
Операторы присваивания
Точка с запятой в конце любой операции присваивания превращает ее в оператор присваивания. Побочное действие операции — присваивание — становится в операторе основным.
The difference between an operation and an assignment operator is only theoretical. An assignment is more commonly used as an operator, not an operation.
Conditional operator
A conditional statement (if-then-else statement) in the Java language is written like this:
if (logVyr) operator1 else operator2
and operates as follows. First, the logical expression log is computed. If the result is true, then the operator is valid ! and on this the action of the conditional statement is completed, statement2 does not work, then the following if statement will be executed. If the result is false, then operator2 acts , with the operator,! not done at all.
The conditional statement can be abbreviated (if-then statement):
if (logVyr) operator!
and if false, nothing is done.
Синтаксис языка не позволяет записывать несколько операторов ни в ветви then, ни в ветви else. При необходимости составляется блок операторов в фигурных скобках. Соглашения "Code Conventions" рекомендуют всегда использовать фигурные скобки и размещать оператор на нескольких строках с отступами, как в следующем примере:
if (а < х) {
х = а + b; } else {
х = а — b;
}
Это облегчает добавление операторов в каждую ветвь при изменении алгоритма. Мы не будем строго следовать этому правилу, чтобы не увеличивать объем книги.
Очень часто одним из операторов является снова условный оператор, например:
if (п == 0}{
sign = 0;
} else if (n < 0){
sign = -1;
} else {
sign = 1;
}
При этом может возникнуть такая ситуация ("dangling else"):
int ind = 5, х = 100;
if (ind >= 10) if (ind <= 20) x = 0; else x = 1;
Сохранит переменная х значение юо или станет равной 1? Здесь необходимо волевое решение, и общее для большинства языков, в. том числе и Java,. правило таково: ветвь else относится к ближайшему слева услдвиюif, не имеющему своей ветви else. Поэтому в нашем примере переменная х останется равной юо.
Изменить этот порядок можно с помощью блока:
if (ind > 10) {if (ind < 20) x = 0; else x = 1;}
Вообще не стоит увлекаться сложными вложенными условными операторами. Проверки условий занимают много времени. По возможности лучше использовать логические операции, например, в нашем примере можно написать
if (ind >= 10 && ind <= 20) х = 0; else х = 1;
В листинге 1.4 вычисляются корни квадратного уравнения ах 2 + bх + с = 0 для любых коэффициентов, в том числе и нулевых.
Листинг 1.4. Вычисление корней квадратного уравнения
class QuadraticEquation{
public static void main (String [] args) {
double a = 0.5, Ъ = -2.7, с = 3.5, d, eps=le-8;
if (Math.abs(a) < eps)
if (Math.abs(b) < eps)
if (Math.abs(c) < eps) // Все коэффициенты равны нулю
System.out.println("Решение —любое число");
else
System.out.println("Решений нет");
else
System.out.println("xl = x2 = " +(-c / b) ) ;
else { // Коэффициенты не равны нулю
if((d = b**b — 4*a*c)< 0.0){ // Комплексные корни
d = 0.5 * Math.sqrt(-d) / a;
a = -0.5 * b/ a;
System.out.println("xl = " +a+ " +i " +d+
",x2 = " +a+ " -i " +d);
} else {
// Вещественные корни
d =0.5 * Math.sqrt(d) / a;
a = -0.5 * b / a;
System.out.println("x1 = " + (a + d) + ", x2 = " +(a - d));
}
}
)
}
В этой программе использованы методы вычисления модуля absо и кш; ратного корня sqrt о вещественного числа из встроенного в Java API класса Math. Поскольку все вычисления-С вещественными числами производятся приближенно, мы считаем, что коэффициент уравнения равен нулю, если его модуль меньше 0,00000001. Обратите внимание на то, как в методе println о используется сцепление строк, и на то, как операция присваивания при вычислении дискриминанта вложена в логическое выражение.
"Продвинутым" пользователям
Вам уже хочется вводить коэффициенты а, b и с прямо с клавиатуры? Пожалуйста, используйте метод System, in. read (byte [ ] bt), но учтите, что этот метод записывает вводимые цифры в массив байтов bt в кодировке ASCII, в каждый байт по одной цифре. Массив байтов затем надо преобразовать в вещественное число, например, методом Double(new String(bt)).doubleValue0 . Непонятно? Но это еще не все, нужно обработать исключительные ситуации, которые могут возникнуть при вводе (см. главу 18).
Comments
To leave a comment
Object oriented programming
Terms: Object oriented programming