1.2 Basic properties of call flows

The main properties of call flows are:

1. Stationarity;

2. Ordinary;

3. Lack of aftereffect.

1. The call flow is called stationary, if the probability of receipt of calls within the time interval [t 0; t0 + Δ t) does not depend on t 0, but depends only on the length of the interval Δ t: Pk (Δt) = const with Δ t = const. Or: Pk (t0, t0 + Δ t) = const with Δ t = const

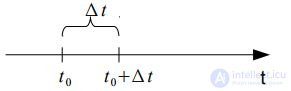
In other words, stationarity means the constancy of the probabilistic behavior of a random variable over time.

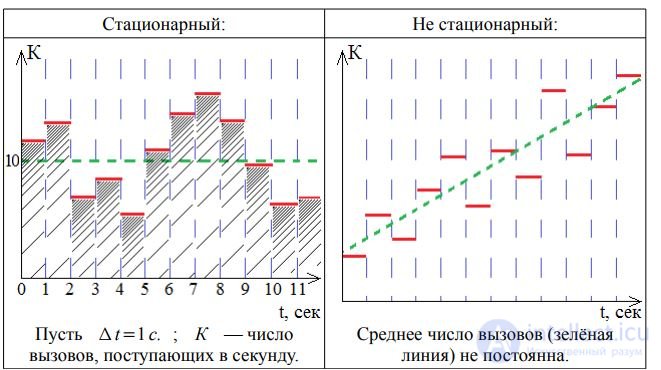
Stationarity means the constancy in time of the density of the onset of calls, that is, the constancy of the average number of calls per unit of time.

2. Call flow is called ordinary if the probability of receiving more than one call in the time interval [t 0; t0 + Δt) at Δ t → 0 and any initial moment t 0 is infinitely small of a higher order than Δ t.

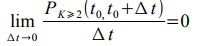
Let us put off the moments of call arrival on the abscissa, and the number of calls to the service system during the time [0, t) - K (t) along the ordinate axis:

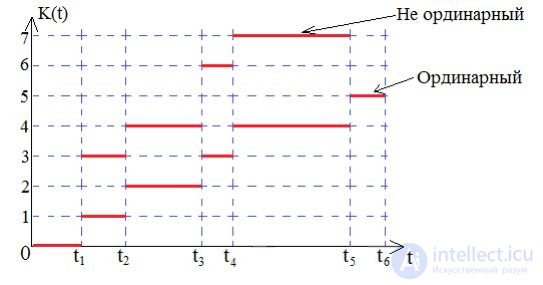
In this course we will consider only ordinary flows.

3. The absence of aftereffect implies that the probability of incoming K calls in the time interval [t 0; t0 + Δt) does not depend on how many calls and how these calls came before t 0: Pk (t0, t0 + Δ t) Obviously, this property is not always satisfied. For example, the call flow at the output of the switching system may depend on the state of the switching system, and, consequently, on how many calls are received by the CS before t 0. Call flows can have either all or only some of these properties. Examples: streams with simple aftereffect, with limited aftereffect, etc.