1.3 Basic Characteristics of Call Flows

The main characteristics of call flows are their intensity and parameter. Let Λ (t) be the mathematical expectation of the number of calls entering the interval [0, t). The function Λ (t) is called the leading stream function.

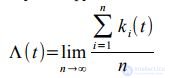
Where n is the number of observations, ki (t) is the number of calls received during the time interval [0, t) in the i -th observation period.

By definition, the instantaneous intensity of the flow is called the limit:

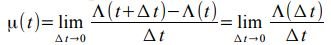
For a stationary flow, the instantaneous intensity is the same at the same time at a given interval. For a stationary flow, the intensity μ is the mathematical expectation of the number of calls arriving in a unit of time.

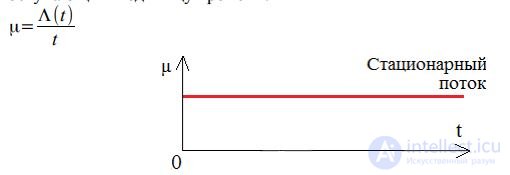
Call Density:

By definition, the call flow parameter λ (t) at time t refers to the ratio of the probability of receiving at least one call in the interval [t, t + Δ t) to the duration of this interval Δ t as Δ t → 0

In other words, the flow parameter is the probability density of incoming calls at time t.

The probability can not be greater than 1.

Probability density can take any positive number.

The stationary flow parameter is constant, independent of time, λ (t) = λ> 0.

For any stationary flow, the inequality μ⩾λ always holds. If the flow is also ordinary, then μ = λ.