Nonlinear programming

Nonlinear programming ( NLP , N on L inear Programming ) is a case of mathematical programming in which the objective function or constraint is a nonlinear function.

The problem of nonlinear programming is posed as the problem of finding the optimum of a certain objective function. 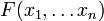under the conditions

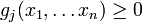
Where 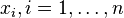- options, 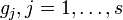- restrictions 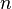- the number of parameters - the number of restrictions.

In contrast to the linear programming problem, in a nonlinear optimum programming problem, it does not necessarily lie on the boundary of the region defined by the constraints.

Methods for solving the problem

One of the methods that allow one to reduce the problem of nonlinear programming to solving a system of equations is the Lagrange method of indefinite multipliers.

If the objective function F is linear and the limited space is a polytope, then the problem is a linear programming problem that can be solved using well-known linear programming solutions.

If the objective function is concave (maximization problem) or convex (minimization problem) and the set of constraints serves as convex, then the problem is called convex , and in most cases, general convex optimization methods can be used.

If the objective function is a ratio of concave and convex functions (when maximized) and constraints are convex, then the problem can be transformed into a convex optimization problem using fractional programming techniques.

There are several methods for solving nonconvex problems. One approach is to use special formulations for linear programming problems. Another method involves the use of branch and bound methods, where the problem is divided into subclasses to be solved with convex (minimization problem) or linear approximations that form the lower limit of the total cost within the section. In the following sections, at a certain point, an actual solution will be obtained, the cost of which is equal to the best lower bound obtained for any of the approximate solutions. This solution is optimal, although perhaps not the only one. The algorithm can be terminated at an early stage, with the certainty that the optimal solution is within the limits of the allowable deviation from the best point found; such points are called ε-optimal. Completion of ε-optimal points, as a rule, is necessary to ensure finite finality. This is especially useful for large, complex tasks and tasks with uncertain costs or values, where uncertainty can be determined from the corresponding reliability estimate.

Differentiation and regularity conditions, the Karush-Kuhn-Tucker conditions (KKT) provide the necessary conditions for optimality of the solution. With convexity, these conditions are also sufficient.