Lecture
Linear programming is a mathematical discipline devoted to the theory and methods of solving extremal problems on sets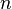 
-dimensional vector space defined by systems of linear equations and inequalities.
Linear programming is a special case of convex programming, which in turn is a special case of mathematical programming. At the same time, it is the basis of several methods for solving problems of integer and non-linear programming. One of the generalizations of linear programming is fractional linear programming.
Many properties of linear programming problems can also be interpreted as properties of polyhedra and thus formulate and prove them geometrically.
Mathematical studies of individual economic problems, the mathematical formalization of numerical material was conducted in the XIX century. Primathematichesky analysis of the process of extended production used algebraic relationships, their analysis was carried out using differential calculus. This made it possible to get a general idea of the problem.
The development of the economy required quantitative indicators, and in the 1920s an inter-sectoral balance (MOB) was created. He then served as the impetus for the creation and study of mathematical models. The development of the MOB in the years 1924-1925 in the USSR influenced the work of the economist and statistics Vasily Vasilyevich Leontyev. He developed an interbranch model of production and distribution of products.
In 1938, Leonid Vitalyevich Kantorovich, in the course of scientific consultation, began to study a purely practical task of drawing up the best plan for loading shelling machines (plywood trust). This task did not yield to the usual methods. It became clear that the task is not random. [one]
In 1939, Leonid Vitalyevich Kantorovich published the paper “Mathematical Methods of Organization and Production Planning” in which he formulated a new class of extremal problems with constraints and developed an effective method for solving them, thus laying the foundations for linear programming.
The study of such problems led to the creation of a new scientific discipline of linear programming and opened a new stage in the development of economic and mathematical methods.
In 1949, the American mathematician George Bernard Danzig developed an effective method for solving linear programming problems (LPP) - the simplex method. [one]
The term "programming" should be understood in the sense of "planning" (one of the English translation of programming ). It was proposed in the mid-1940s by George Danzig, one of the founders of linear programming, even before computers were used to solve linear problems of optimization.
The method of interior points was first mentioned by I. I. Dikin in 1967. [2]
A common (standard) linear programming problem is the problem of finding the minimum of a linear objective function (linear form) of the form [3] :
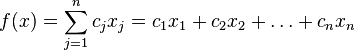
The task in which restrictions in the form of inequalities appear is called the main linear programming problem (OZLP)
,
.
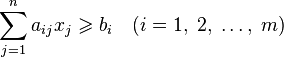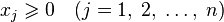A linear programming problem will have a canonical form if, in the main problem, instead of the first system of inequalities, there is a system of equations with constraints in the form of equality [4] :
,
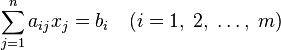The main task can be reduced to the canonical way of introducing additional variables.
Linear programming problems of the most general form (problems with mixed constraints: equalities and inequalities, the presence of variables free of constraints) can be reduced to equivalent (having the same set of solutions) variable changes and replacing equalities by a couple of inequalities [5] .
It is easy to see that the task of finding the maximum can be replaced by the task of finding the minimum, taking the coefficients 
with the opposite sign.
Consider the problem of maximum matching in a bichrophic graph: there are several boys and girls, and for each of the boys and girls it is known whether they are cute to each other. It is necessary to marry the maximum number of couples with mutual sympathy.
We introduce variables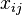 
that match a pair of 
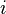of that young man and 
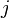-this girl and satisfy the restrictions:
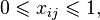
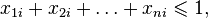
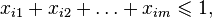
with objective function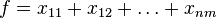 
. It can be shown that among the optimal solutions of this problem there is an integer. Variables equal to 1 will match the pairs to be married.
Suppose there is a graph (with oriented edges) in which its capacity is indicated for each edge. And two vertices are set: the drain and the source. For each edge, it is necessary to specify how much liquid will flow through it (no more than its throughput) so as to maximize the total flow from the source to the drain (liquid cannot appear or disappear in all vertices except the source and drain, respectively).
Take as variables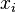 
- the amount of fluid flowing through 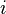-th edge. Then
,
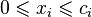Where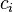 
- throughput 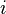of that rib These inequalities must be supplemented by the equality of the amount of inflowing and outflowing fluid for each vertex, except for the drain and the source. As a function 
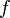It is natural to take the difference between the amount of leakage and inflowing fluid in the source.
The generalization of the previous problem - the maximum flow of the minimum cost. In this problem, the costs are given for each edge and you need to select the flow with the minimum cost among the maximum flows. This task is reduced to two linear programming problems: first you need to solve the maximum flow problem, and then add the constraint to this problem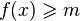 
where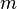 
- the value of the maximum flow, and solve the problem with the new function 
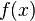- stream cost.
These problems can be solved faster than by general algorithms for solving linear programming problems, due to the special structure of equations and inequalities.
There is some kind of uniform cargo that needs to be transported with 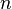warehouses on 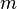factories. For each warehouse 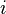know how much cargo is in it 
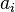, and for each plant its need is known 
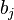in the load. The cost of transportation is proportional to the distance from the warehouse to the plant (all distances 
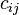from 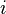-th warehouse to 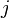th plant are known). Required to make the cheapest transportation plan.
The decisive variables in this case are 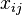- the amount of cargo transported from 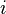on stock 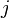plant They satisfy the constraints:
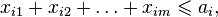
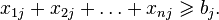
The objective function is: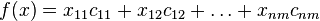 
to be minimized.
There is a matrix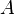 
size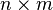 
. The first player chooses a number from 1 to 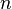second from 1 to 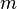. Then they compare the numbers and the first player gets 
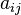points and the second 
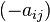points ( 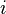- the number chosen by the first player 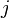- the second). It is necessary to find the optimal strategy of the first player.
Let in the optimal strategy, for example, the first player number 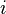need to choose with probability 
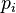. Then the optimal strategy is the solution to the following linear programming problem:
,
,
( 
),
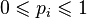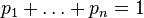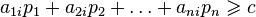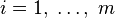in which you need to maximize the function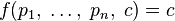 
. Value in the optimal solution it will be the mathematical expectation of winning the first player in the worst case.
The most well-known and widely used in practice for solving a general linear programming (LP) problem is the simplex method. Despite the fact that the simplex method is a fairly effective algorithm that has shown good results in solving applied LP problems, it is an algorithm of exponential complexity. The reason for this is the combinatorial character of the simplex method, which sequentially iterates over the vertices of a polyhedron-admissible solutions when searching for the optimal solution.
The first polynomial algorithm, the ellipsoid method, was proposed in 1979 by the Soviet mathematician L. Khachiyan, thus solving a problem that remained unsolved for a long time. The ellipsoid method has a completely different, non-combinational nature than the simplex method. However, in computational terms, this method proved unpromising. Nevertheless, the very fact of the polynomial complexity of the problems led to the creation of a whole class of efficient LP algorithms — inner point methods , the first of which was N. Karmarkar’s algorithm proposed in 1984. Algorithms of this type use continuous interpretation of the LP problem, when instead of iterating over the vertices of a polyhedron, solutions of the LP problem are searched along the trajectories in the space of variables of the problem that do not pass through the vertices of the polyhedron. The interior point method, which, unlike the simplex method, bypasses points from the inside of the range of permissible values, uses the methods of logarithmic barrier functions of nonlinear programming developed in the 1960s by Fiacco and McCormick.
Comments
To leave a comment
Math programming
Terms: Math programming