Lecture
The Meet-in-the-Middle attack (MITM) is a generic space – time tradeoff cryptographic attack.
MITM is a generic attack, applicable to several cryptographic systems. This is a system that is therefore unimportant to this attack.
The attacker decides that he will be able to encrypt and decrypt, and the corresponding ciphertexts.
For example, it can be easy to use the cipher system. If you want to go through.
This is a scattering of ideas for a group of players. As the backward mapping (inverse image) through the last functions of the composed function.
The Multidimensional MITM (MD-MITM) uses the combination of several simultaneous MITM attacks.
If you’re trying to find out how to use it, it would take you a few seconds to get rid of the keys. MITM or MD-MITM
It was first developed as an attack on an expansion of a block cipher by Diffie and Hellman in 1977. [1]
However, he has been deviating the single-encryption scheme.
In 2011, Bo Zhu and Guangdong GOST, KTANTAN and Hummingbird-2. [2]
Assume the attacker knows the following:
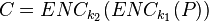
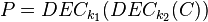
where the decryption function is defined as the ENC -1 (inverse mapping) and the 1 and k 2 are two keys.
If you can, then you can follow the decrypt decrypt cchertext by comp. The matches the keys. (To speed up the comparison, the ENC k 1 (P) can be matched, then the DEC 2 (C) can be matched)
"Double DES" doesn’t provide space for any reason. [3] However, Triple DES with a "triple length" (168-bit) space and 2 112 operations. [four]
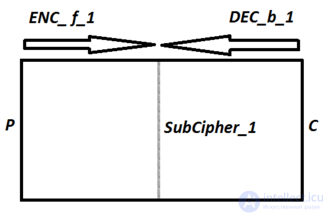
Once the matches are discovered, they can be verified with a test-set of plaintext and ciphertext.
Compute the following:
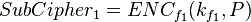 ∀
∀ 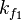 ∈
∈ 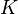 :
:and save each 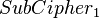 together with corresponding
together with corresponding 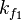 in a set A
in a set A
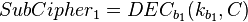 ∀
∀ 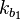 ∈
∈ 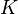 :
:and compare each new 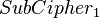 with the set A
with the set A
When a match is found, keep the k f 1 , k b 1 as a candidate key-pair in a table T. Test pairs in pairs for each pair of (P, C) to confirm validity. If the key-pair doesn’t work again, do MITM again on a new pair of (P, C) .
If this is a key, this attack uses a combination of 2k + 1 ( 2k ) , which needs 2 2 · k encryptions but O (1) space.
It is defined as the following: where the decryption and the decryption have been made. MD-MITM . This is the most preferred encryption option. There are several ways to try to achieve this goal. [2]
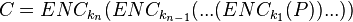
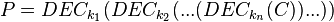
that is a plaintext P is encrypted multiple times using the same block cipher

The MD-MITM has been used, where it has been shown. [2]
Compute the following:
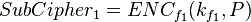 ∀
∀ 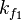 ∈
∈ 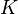 :
:and save each 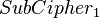 together with corresponding
together with corresponding 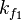 in a set
in a set 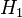 .
.
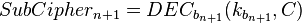 ∀
∀ 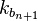 ∈
∈ 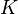 :
:and save each 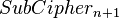 together with corresponding
together with corresponding 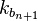 in a set
in a set 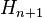 .
.
For each possible guess on the intermediate state 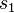 compute the following:
compute the following:
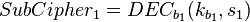 ∀
∀ 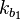 ∈
∈ 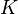 :
:and for each match between this 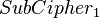 and the set
and the set 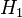 save
save 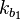 and
and 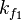 in a new set
in a new set 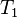 .
.
 ∀
∀ 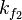 ∈
∈ 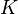 :
:and save each 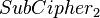 together with corresponding
together with corresponding 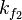 in a set
in a set 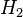 .
.
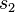 compute the following:one
compute the following:one 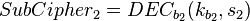 ∀
∀ 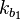 ∈
∈ 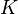
and for each match between this 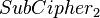 and the set
and the set 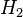 , check also whether
, check also whether
it matches with 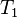 save the combination of sub-keys together in a new set
save the combination of sub-keys together in a new set 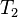 .
.
2 ...
For each possible guess on an intermediate state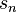 compute the following:a)
compute the following:a) 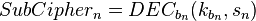 ∀
∀ 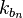 ∈
∈ 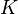
and for each match between this 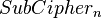 and the set
and the set 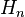 , check also whether
, check also whether
it matches with 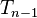 save
save 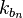 and
and 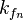 in a new set
in a new set
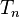 .
.
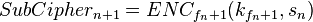 ∀
∀ 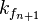 ∈
∈ 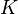
and for each match between this 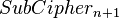 and the set
and the set 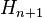 , check also
, check also
whether it matches with 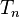 . If this is the case then: "
. If this is the case then: "
Use the found combination of sub-keys 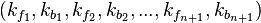 on the pair of plaintext / ciphertext to verify the correctness of the key.
on the pair of plaintext / ciphertext to verify the correctness of the key.
Note the nested element in the algorithm. It is not possible to make a guess. This is an MD-MITM attack.
Brute force, is 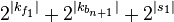 ⋅
⋅ 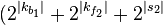 ⋅
⋅ 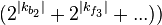
It is easy to see that 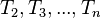 less than the first built table of candidates values:
less than the first built table of candidates values: 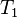 as i increases
as i increases 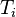 it will be up to the end destination.
it will be up to the end destination. 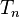 .
.
An upper bound of the memory of MD-MITM is then

where 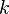 denotes the whole key (combined).
denotes the whole key (combined).
Keynote (may be false positive), which is 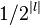 where
where 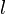 is the intermediate state in the first MITM phase. The size is often the same! Considering it for the first MITM-phase, it is
is the intermediate state in the first MITM phase. The size is often the same! Considering it for the first MITM-phase, it is 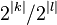 .
.
Therefore, after the first MITM phase, there are 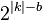 ⋅
⋅ 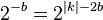 where $ | b | $ is the block size.
where $ | b | $ is the block size.
This is a keynote for each of the keys. 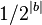 .
.
Brute force 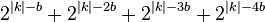 ...
...
, it’s clearly the number of tends to zero.
Conclusion 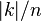 ⌉ (P, C) -pairs.
⌉ (P, C) -pairs.
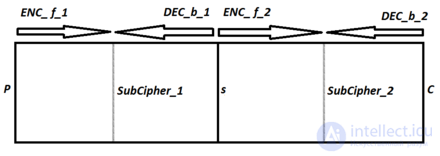
The 2D MITM is mounted:
2D-MITM is mounted on a block cipher encryption.
In Two-Dimensional MITM (2D-MITM) See below figure:
Compute the following:
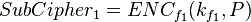 ∀
∀ 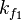 ∈
∈ 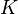
and save each 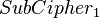 together with corresponding
together with corresponding 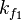 in a set A
in a set A
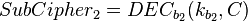 ∀
∀ 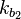 ∈
∈ 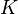
and save each 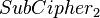 together with corresponding
together with corresponding 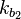 in a set B.
in a set B.
For each possible guess on an intermediate state s between 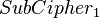 and
and 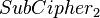 compute the following:
compute the following:
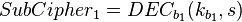 ∀
∀ 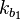 ∈
∈ 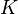
and for each match between this 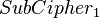 and the set A, save
and the set A, save 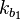 and
and 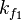 in a new set T.
in a new set T.
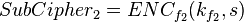 ∀
∀ 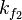 ∈
∈ 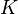
and for each match between this 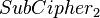 and the set B, check
and the set B, check
if this is the case then:
Use the found combination of sub-keys 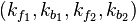 on the pair of plaintext / ciphertext to verify the correctness of the key.
on the pair of plaintext / ciphertext to verify the correctness of the key.
Brute force, is 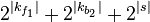 ⋅
⋅ 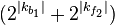 where | ⋅ | denotes the length.
where | ⋅ | denotes the length.
A and B, where T is much smaller than the others.
For data transmission see for MD-MITM.
Comments
To leave a comment
Cryptanalysis, Types of Vulnerability and Information Protection
Terms: Cryptanalysis, Types of Vulnerability and Information Protection