Lecture
Genetic algorithm (born genetic algorithm ) is a heuristic search algorithm used to solve optimization and simulation problems by randomly selecting, combining and varying the desired parameters using mechanisms similar to natural selection in nature. It is a type of evolutionary computation that solves optimization problems using natural evolution methods such as investigation, mutation, selection, and crossing-over. A distinctive feature of the genetic algorithm is the emphasis on the use of the "crossing" operator, which performs the operation of recombination of candidate solutions, whose role is similar to the role of crossing in living nature.
The first work on the simulation of evolution was carried out in 1954 by Niels Baricelli on a computer installed at the Institute of Advanced Studies, Princeton University. [1] [2] His work, published the same year, attracted widespread public attention. Since 1957, [3] the Australian geneticist Alex Fraser has published a series of studies on the simulation of artificial selection among organisms with multiple control of measurable characteristics. This allowed the computer simulation of evolutionary processes and the methods described in the books of Frazer and Barnell (1970) [4] and Crosby (1973). [5] , from the 1960s become a more common activity among biologists. Fraser’s simulations included all the essential elements of modern genetic algorithms. In addition to this, in the 1960s, Hans-Joachim Bremermann published a series of papers that also adopted the approach of using a population of solutions subjected to recombination, mutation, and selection in optimization problems. Bremermann's research also included elements of modern genetic algorithms. [6] Among other pioneers, it should be noted Richard Friedberg, George Friedman and Michael Conrad. Many early works were reprinted by David B. Vogel (1998). [7]
Although Baricelli, in his 1963 paper, simulated the ability of a machine to play a simple game, [8] artificial evolution became a generally accepted optimization method after the work of Ingo Rechenberg and Hans-Paul Schwefel in the 1960s and early 1970s of the twentieth century - the Rechensberg group was able to solve complex engineering problems according to evolution strategies. [9] [10] [11] [12] Another approach was the technique of evolutionary programming by Lawrence J. Vogel, which was proposed for creating artificial intelligence. Evolutionary programming originally used finite automata to predict circumstances, and used diversity and selection to optimize the prediction logic. Genetic algorithms became especially popular thanks to the work of John Holland in the early 70s and his book Adaptation in Natural and Artificial Systems (1975) [13] . His research was based on experiments with cellular automata conducted by Holland and his writings at the University of Michigan. Holland introduced a formalized approach to predicting the quality of the next generation, known as the Theorem of Schemes. Research on genetic algorithms remained largely theoretical until the mid-80s, when the First International Conference on Genetic Algorithms was finally held in Pittsburgh, Pennsylvania (USA).
With the growth of research interest, the computing power of desktops has also grown substantially; this has made it possible to use new computing equipment in practice. In the late 80s, General Electric began selling the world's first product that worked using a genetic algorithm. They became a set of industrial computing tools. In 1989, another company Axcelis, Inc. released Evolver - the world's first commercial product based on a genetic algorithm for desktop computers. Technological journalist The New York Times, John Markoff, wrote about Evolver in 1990.
The task is formalized in such a way that its solution can be encoded as a vector (“genotype”) of genes, where each gene can be a bit, a number, or some other object. In classical GA implementations, it is assumed that the genotype has a fixed length. However, there are variations of HA free from this limitation.
In some, usually random, ways, many genotypes of the initial population are created. They are evaluated using the “fitness function”, as a result of which a certain value is associated with each genotype (“fitness”), which determines how well the phenotype described by it solves the set task.
When choosing the “fitness function” (or fitness function in the English literature), it is important to ensure that its “relief” is “smooth”.
From the resulting set of solutions (“generations”), taking into account the value of “fitness”, solutions are selected (usually the best individuals are more likely to be selected), to which “genetic operators” are applied (in most cases “crossing” - crossover and “mutation” - mutation ), resulting in new solutions. For them, the value of fitness is also calculated, and then the selection (“selection”) of the best decisions in the next generation is made.
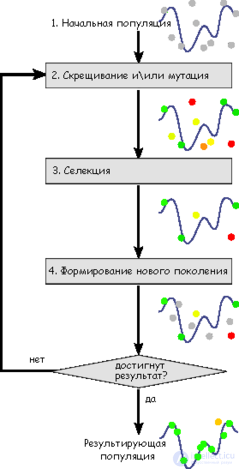
This set of actions is repeated iteratively, so the “evolutionary process” is modeled, which lasts several life cycles ( generations ) until the criterion for stopping the algorithm is fulfilled. Such a criterion may be:
Genetic algorithms are mainly used to search for solutions in multidimensional search spaces.
Thus, the following stages of the genetic algorithm can be distinguished:
Before the first step, you need to randomly create an initial population; even if it turns out to be completely uncompetitive, it is likely that the genetic algorithm will still rather quickly translate it into a viable population. Thus, in the first step, you can not especially try to make too fit individuals, it is enough that they match the format of individuals of the population, and they can be calculated fitness function (Fitness). The result of the first step is the population H, consisting of N individuals.
Reproduction in genetic algorithms is usually sexual - to produce a descendant, we need several parents, usually two.
Reproduction in different algorithms is determined differently - it, of course, depends on the presentation of the data. The main requirement for reproduction is that the descendant or descendants have the opportunity to inherit the traits of both parents, “mixing” them in some way.
Why are individuals for breeding usually chosen from the entire population of H, and not from the surviving elements of H 0 in the first step (although the latter also has a right to exist)? The fact is that the main scourge of many genetic algorithms is the lack of diversity (diversity) in individuals. The single genotype, which is a local maximum, is rather quickly distinguished, and then all elements of the population lose to it, and the entire population is “hammered” by copies of this individual. There are different ways to deal with such an undesirable effect; one of them is the choice for breeding of not the fittest, but generally all individuals.
Mutations are all the same as reproduction: there is a certain proportion of mutants m, which is a parameter of the genetic algorithm, and at the mutation step you need to select mN individuals, and then change them in accordance with pre-determined mutation operations.
At the selection stage, it is necessary to select a certain proportion of it from the entire population, which will remain “alive” at this stage of evolution. There are different ways to conduct a selection. The probability of survival of an individual h should depend on the value of the fitness function h (h). The proportion of surviving s is usually a parameter of the genetic algorithm, and it is simply set in advance. According to the results of the selection of N individuals, the population H should remain sN individuals, which will be included in the final population H '. The remaining individuals perish.
There are several reasons for criticism about the use of a genetic algorithm in comparison with other optimization methods:
There are many skeptics about the desirability of using genetic algorithms. For example, Stephen S. Skien, a professor at the Department of Computer Engineering at Stony-Brooke University, a well-known researcher of algorithms, winner of the IEEE Institute Prize, writes [16] :
 | I personally have never come across a single task, for which genetic algorithms would prove to be the most appropriate means. Moreover, I have never met any results of calculations obtained by means of genetic algorithms that would make a positive impression on me. |  |
Genetic algorithms are used to solve the following tasks:
Search in one-dimensional space, without crossing.
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <iostream>
#include <numeric>
int main ()
{
srand ((unsigned int) time (NULL));
const size_t N = 1000;
int a [N] = {0};
for (;;)
{
// mutation to the random side of each element:
for (size_t i = 0; i <N; ++ i)
a [i] + = ((rand ()% 2 == 1)? 1: -1);
// now choose the best, sorted in ascending order
std :: sort (a, a + N);
// and then the best will be in the second half of the array.
// copy the best ones in the first half, where they left offspring, and the first ones died:
std :: copy (a + N / 2, a + N, a);
// now look at the average state of the population. As you can see, it is getting better and better.
std :: cout << std :: accumulate (a, a + N, 0) / N << std :: endl;
}
}
Search in one-dimensional space with the probability of survival, without crossing. (tested on Delphi XE)
program program1;
{$ APPTYPE CONSOLE}
{$ R * .res}
uses
System.Generics.Defaults,
System.Generics.Collections,
System.SysUtils;
const
N = 1000;
Nh = N div 2;
var
A: array [1..N] of Integer;
I, R, C, Points, BirthRate: Integer;
Iptr: ^ Integer;
begin
Randomize;
// Partial population
for I: = 1 to N do
A [I]: = Random (2);
repeat
// Mutation
for I: = 1 to N do
A [I]: = A [I] + (-Random (2) or 1);
// Selection, best at the end
TArray.Sort <Integer> (A, TComparer <Integer> .Default);
// Preset
Iptr: = Addr (A [Nh + 1]);
Points: = 0;
BirthRate: = 0;
// Crossing Results
for I: = 1 to Nh do
begin
Inc (Points, Iptr ^);
// Random crossing success
R: = Random (2);
Inc (BirthRate, r);
A [I]: = Iptr ^ * R;
Iptr ^: = 0;
Iptr: = Ptr (Integer (Iptr) + SizeOf (Integer));
end;
// Subtotal
Inc (C);
until (Points / N> = 1) or (C = High (Integer));
Writeln (Format ('Population% d (rate:% f) score:% f', [C, BirthRate / N, Points / N]));
end.
Comments
To leave a comment
Evolutionary algorithms
Terms: Evolutionary algorithms