Gene Expression Programming: Genetic Operators

Introduction Evolutionary algorithms (EA) represent a direction in artificial intelligence, using and modeling biological evolution. Among EA, stochastic and including evolutionary programming, evolutionary strategies, genetic algorithms, genetic programming, in particular, programming with gene expression, genetic algorithms are the most common (GA). GA is a machine learning method based on selection mechanisms in nature, which conduct a random and parallel search for solutions that optimize a predetermined fitness function. Genetic programming (GP) was created as an independent direction in the field of evolutionary computations, despite the fact that this method can also be interpreted as a special class of GA. The main mechanisms of selection, recombination, and mutation are adapted and applied in the GP in a similar manner. A more general representation of problems in a GP allows you to define an individual of a population as a structure, formula, or even more generally as a program. This allows us to consider new areas of application of EA. The difference between GA and GP is not expressed strongly: both systems use the same type of objects, which serves as both a genotype and a phenotype. This approach has one of two limitations: the simplicity of applying genetic operators to objects means their insufficient expressiveness and complexity of these objects.

com (in the case of GA), and their complexity leads to difficulties in reproduction and modification (in the case of GP). Programming with gene expression (PEG) is implemented using the algorithm [1]: 1. Creating an initial population 2. Decoding individuals 3. Performing programs of individuals 4. Calculating the fitness function (FF) of individuals 5. Checking the stopping criterion of the algorithm (the required accuracy is reached limited runtime has elapsed) 6. Copying the best individual (elitism) 7. Selection 8. Replication 9. Mutation 10. Transfer operators 11. Operators of recombination 12. Return to item 2 In PEG, the following operators are used: replication, mutation, copying with a shift copied I shifted to the root, interchanging genes ki, one- and two-point recombination, gene recombination. Replication is the simplest operator that does not introduce diversity into the genome and is used in tandem with the selection operator to copy individuals into the new population in accordance with the FF value and the frequency introduced by the roulette operator. Mutation (replacement of a symbol - an element of the gene corresponding to a tree node) can occur anywhere on a chromosome. The operator's probability, as a rule, is set equivalent to two mutations in the chromosome. Elements,

susceptible mutations in the head of a gene, can be changed to any other symbol (function or terminal), in the tail - only to the terminal. This restriction should ensure the preservation of the chromosome structure and ensure decoding of the syntactically correct tree. Among all modifying operators, mutation is the most significant and effective, since unlike the rest, combining existing genome regions, the mutation is aimed at creating new elements, and therefore introduces the most radical changes, expanding the search for solutions . Recombination - an operation to move successive sections of the genome within the chromosome. The purpose of this article is to study the influence of the choice of genetic operators on the properties of the PEG algorithm. The paper [2] describes a method for evaluating the efficiency of modifications of the PEG algorithm, which consists in statistically processing the results of multiple launches in order to obtain the mean square error (CKO) of the best model among all launches (eb) and the share of successful launches (rf), t. e. those during which the model was obtained with acceptable accuracy for this task. For testing, we used models of sinusoid (sin), Rosenbrock function (rosen), and the sum of four sigmoids (sigmas). The same methodology and models are used in this work to compare genetic operators.

Selection operators

The process of evolution is based on genetic variation and selection procedure. These mechanisms are involved in all evolutionary algorithms. However, the method of ensuring genetic variability, which could be called the best, has not been identified. Researchers divide these methods into mutations and recombination. The success of the evolution also significantly depends on the genetic operators used by the algorithm, the size and composition of the initial population.

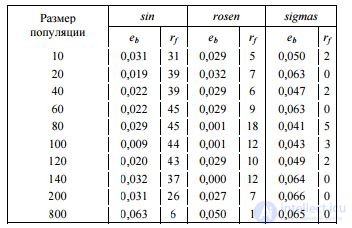
When comparing the efficiency of the standard (traditional) PEG algorithm for different population sizes, it should be taken into account that the execution time of the algorithm is directly proportional to the population size. Therefore, in order to estimate this factor in conditions of limited time, each start-up was assigned a fixed operating time, so that algorithms with a large population size could calculate a smaller number of generations. The experimental results for different numbers of individuals are given in Table. 1, indicate the presence of a peak efficiency at a population size of 80–120 individuals.

T of the bar a 1. The efficiency of the algorithm with different population sizes

One of the most important applications of PEG is a symbolic regression, the purpose of which is to search for the expression that most corresponds to known setpoints with a certain error. Setting a small value (absolute or relative) to the permissible error allows one to find good solutions to some mathematical problems, but in most cases, setting a small error slows down the evolution process due to a more rigorous selection of individuals. If, on the other hand, a too large admissible error is specified, a large number of individuals will be selected, which are not acceptable solutions, but the FF value of which will be very high. Individuals in PEG are selected by the proportional roulette operator with simple elitism: the best individual of the population is

worn in the next generation, the chances of the rest are directly proportional to the values ​​of their FF. This form of elitism ensures the preservation of the best solution found. Each roulette start selects one individual, respectively, the number of roulette starts is equal to the population size. After selection of a new population, genetic operators are applied in turn to be applied to randomly selected individuals. For example, if the operator’s probability is 70 percent, then seven out of 10 individuals will be modified by it. Each individual can be modified at once by several operators, each of which can be applied to the individual only once. This distinguishes PEG from genetic programming (GP), in which an individual is not changed by more than one operator per iteration. The offspring thus obtained is significantly different from the parent individuals. The most universal selection operator with sufficient efficiency used in PEG will be the roulette algorithm, in which the probability of further participation of an individual in the evolution process is directly determined by the value of its FF, which leads to the preservation of individuals only with a high FF value. However, if the FF value of one of the individuals of the population at a certain moment significantly exceeds the FF value of the others, this leads to the algorithm getting stuck in the local optimum and losing many individuals with a tendency to improve with small current FF values. In [3], a selection formula was proposed, borrowed from immune algorithms and based on the concept of density D individuals

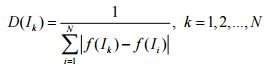
and it is suggested that this selection formula guarantees a variety of genetic material in the population. Here N is the number of individuals in the population; f - fitness function. The density values ​​are then used to calculate the sampling probability.

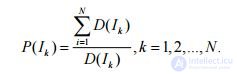
Thus, the more individuals are similar (by the criterion of probability) to the individual k I, the less likely it is of selection. However, the authors do not note the fact that, with this approach, individuals with fundamentally different syntactic trees, but equal values ​​of FF, will be indistinguishable from each other. Comparison of different approaches to the selection mechanism is presented in Table. 2. In this and in

Table 2. Efficiency of an algorithm with various selection operators and population sizes

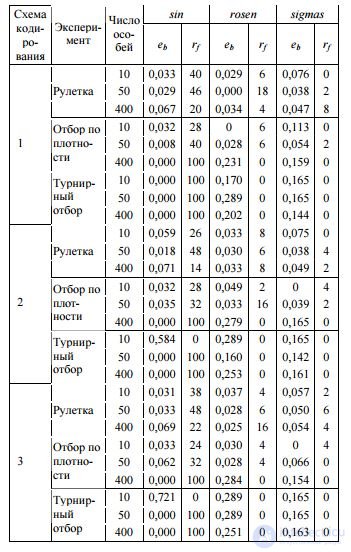
In the following tables in the “Coding scheme” column, the number 1 corresponds to the traditional

mu coding, 2 - prefix, 3 - coding with overlay. In all cases, the implementation of simple elitism was carried out by preserving the best individual. An analysis of these results leads to certain conclusions. First, it is advisable to use a population of 50 individuals: this experimentally obtained optimal value is characteristic of all nine experiments performed. Secondly, the traditional PEG algorithm (with coding by traversing the graph in width) reaches its maximum performance when using tournament selection. Third, for PEG overlap, density selection is optimal. Fourth, the best results are shown by the use of prefix PEG in combination with the roulette operator. So, considering the selection operators regardless of the coding method, we can conclude that the choice of the roulette operator will be optimal, as was suggested by the author of the traditional PEG algorithm [1].

Mutation operator

Influence on the dynamics of evolution. In systems based on genotype and phenotype, the search space is separated from the solution space, which significantly improves the performance of such systems. The less restrictions are imposed on the procedure of genotype projection on the phenotype and vice versa, the more effective is the system, since almost any operator, including a mutation, can be used to study the search space. Thus, for example, in the DGP (Developmental Genetic Programming - GP with the development [4]) system, as a result of the translation of a genotype into a phenotype, a syntactically correct tree is not always obtained, which leads to additional operations to remove unsuitable individuals. Therefore, the mutation in DGP does not exceed the crossover operators in terms of indicators. In work [5], to compare the efficiency of genetic operators used in PEG, the dynamic data of the evolution process were compared: the graphs of the FF values ​​of the best individual over the generations (iterations) and the graphs of the average FF values ​​of the population.

During the search for a model created by the formula y (x) = x 4 + x 3 + x 2 + x, the evolutionary process dynamics was studied with different values ​​of the probability of using the mutation operator (pm1, pm2, pm3, pm4). The obtained FF values ​​are shown in Fig. 1. a b c

Fig. 1. Dynamics of evolution with different probabilities of mutation

In fig. 1a, it can be seen that the graph of the best values ​​of FF practically coincides with the graph of average values ​​of FF, especially in the late generations. Such populations are called moderately innovative because of the small difference between individuals and the slow process of evolution. The probability of successful detection of a solution to a problem (the ratio of launches, during which the solution was found, to the total number of launches of the algorithm) set in the experiment was 16 percent. In fig. 1b, it is noticeable that the shape of the graphs coincides (without taking into account the coloration of *** graphs of average FF values), however, they do not intersect, there is a gap between them. The percentage of successful launches was 47 percent. Such a model of evolution is healthy, but weak. With an increase in the probability of mutation, the success of the algorithm increases, reaching a maximum at pm3 = 0.1, shown in Fig. 1, in and appropriate healthy and strong model.

This case is characterized by a larger gap between the graphs, however, the upward trend in the average FF value remains. Finally, the last reduced dynamics with an average FF value at a constant low level with small numbers *** serves as an example of a completely chaotic system, in which, despite elitism, each generation is essentially random. The study of recombination operators as the only sources contributing to genetic diversity revealed a process of population averaging — a rapid reduction in the gap between the best and average FF graphs with their subsequent overlapping. This means that the genome of all individuals of the population is the same, and diversity has been eliminated, which is a consequence of the premature convergence of this approach to the local optimum. In an initial population filled with randomly created features, viable solutions are a rare event, especially when solving complex problems. A successful approach in this case is the beginning of the process of evolution with one or several individual founders [6]. The founder effect, described by E. Mayr as the creation of a new population from the founder individuals, can be initiated by gene drift — a change in the frequency of gene variants due to random processes and selection operators. An example of the most pronounced case of the effect of the founder is the colonization of the uninhabited area (creation of a new population) by one individual. This means that with a certain value of the mutation probability, it is possible to achieve maximum performance of the entire algorithm. In addition, the mutation operator reduces the tendency of the population to homogenize (loss of diversity) and eliminates the strong dependence of the efficiency of the algorithm on the population size. Impact on performance. The effect of the most probable values ​​of the average number of mutations in the chromosome on the operation of algorithms with various methods of encoding syntax trees is shown in Table. 3

We note the efficiency maximum for all coding methods with one or two mutations per chromosome. In the case of PEG with overlaps, the maximum efficiency is much more difficult to isolate, but there is still a drop in productivity with more than two mutations. Therefore, in the following experiments, the value of two mutations will be used.

Modifications

The most significant drawback of the PEG algorithm is its tendency to premature convergence to a local optimum; therefore, any technique aimed at solving this problem leads to a significant increase in the performance of PEG, which is reflected in a reduction in the convergence time, improvement the average fitness of decisions and increase the probability of successful discovery of the optimal solution. To enhance the ability of the algorithm to search, the following dynamic DM-GEP mutation algorithm was proposed in [7]. With the maximum number of T generations, the process of evolution is divided into three phases:  Initial phase: generations from the first to T1.0

 Metaphase: generations from T1 to T2, T1 The probability of mutation pm increases every
five generations from a value of 0.022 to 0.66 s
step 0,002.
 Anaphase: generations from T2 to T. Probably
the pm mutation decreases every ten
generations from 0.066 to 0.022 in increments
0,001.
In [8], it was proposed to use di
the installation of the mutation probability
as the most destructive operator doing
its individual for each individual and
Sims from FF individuals. The higher the FF individuals, the
the more it is adapted, the more heed
required to pay local search
less likely to mutate is established.
    max min min () 1 () / 1000, mm mm mp I fI ppp    
where 1000 is the maximum fitness value;
min 0.044 mp and max 0.1 mp - lower and upper
the limits of probability of mutations, respectively.
The performance of PEG is significantly lower.
depends on the given probabilities of using
non-tic operators. Reduce the impact of these
values ​​for the operation of the algorithm can be
approach of choosing a new value,
In addition, in the annealing simulation method [9], the essence of
the second is to use dependent
time (iteration numbers of the algorithm)
T meter, called temperature. The higher
temperature at a given time, those
more likely to replace the original individual,
obtained by applying genetic
operator. System temperature decreases
with each subsequent iteration,
search for environs of the global optimum
ma in the first phase of the algorithm and leading then to
clarify its location. Speed ​​is
lowering the temperature is controlled by some
parameter a.
With this approach, at each iteration of the
PEG gorm to all parents old
consistently applied genetic
operators, each of which generates a
new child Subsidiary
takes the place of the parent in the population when
the following condition:

min 1, 0,1, if old f new T e random                  where f (old), f (new) - FF of the parent and child individuals, respectively ; random[0, 1] – слу- чайная величина в диапазоне [0, 1]; Ti – тем- пература на i-й итерации алгоритма. Данная модификация позволила несколько улучшить эффективность ПЭГ. Операторы рекомбинации Эти операторы перемещают последователь- ные участки генома в пределах хромосомы. Три типа таких участков накладывают различ- ные ограничения на операторы. Оператор копирования со сдвигом копирует последовательность символов генома в любую позицию головы гена, кроме первой. Ограни- чение на первую позицию обусловлено тем, что перемещаемая последовательность может начинаться с терминального символа, помеще- ние которого в корень приведет к вырожден- ному дереву из одного элемента. Ген–источник копируемой последовательности остается не- изменным. Элементы головы гена–приемника, начиная с позиции, в которую будет скопиро- вана целевая последовательность, сдвигаются для освобождения места, а вышедшие за пре- делы головы элементы отбрасываются. Оператор копирования со сдвигом в корень отличается от предыдущего тем, что целевая последовательность начинается с элемента– функционала и копируется в корень гена– приемника. Оба оператора копирования вносят значительные изменения и поэтому наравне с мутацией отлично подходят для внесения ге- нетического разнообразия, предотвращая за- стревание в локальном оптимуме и ускоряя поиск хороших решений. Оператор перестановки генов вносит изме- нения в результат вычисления декодированно- го дерева только при условии использования некоммутативной связующей функции в муль- тигенной хромосоме, такой как «ЕСЛИ, ТО». Однако преобразующая сила (способность вносить генетическое разнообразие) данного оператора наиболее проявляется в связке с опе-

раторами кроссовера. Например, возможно по- явление дублируемых генов – явление, выпол- няющее ощутимую роль в биологии и эволюции. Все три вида рекомбинации осуществляют обмен генетическим материалом между двумя родительскими хромосомами, порождая две новые особи. Вероятность того, что будет при- менен один из трех описанных далее операто- ров, обычно задают величиной 0,7. В операторе одноточечной рекомбинации две особи скрещиваются вокруг линии, проходя- щей через случайным образом выбранную по- зицию хромосомы. В большинстве случаев полученное потом- ство проявляет характеристики своих родите- лей, что делает одноточечную рекомбинацию наиболее часто используемым в ПЭГ операто- ром, наравне с мутацией. Отличие двухточечной рекомбинации со- стоит в том, что обмен участками генома про- исходит между двумя точками. Поскольку преобразующая сила двухточечной рекомби- нации выше, чем у одноточечной, она приме- няется чаще для решения сложных задач с ис- пользованием мультигенных хромосом. В генной рекомбинации проводится замена генов, занимающих в обеих хромосомах пози- цию, определяемую случайным образом. Следует отметить, что использование реком- бинации и/или операторов перемещения как единственного вида применяемых операторов сводится к перемешиванию существующих участков генома и не обеспечивает создание нового генетического материала. Поэтому для решения сложных задач в таком случае может понадобиться популяция большого размера.

Числовые константы в ПЭГ

Создание числовых констант с плавающей запятой необходимо для выполнения символь- ной регрессии. В стандартном алгоритме ПЭГ для обозначения константы в геноме использу- ется терминальный символ «?», а начальный набор констант представлен доменом DC [10]. Каждый ген располагает собственным масси- вом, содержащим используемые им константы и заполняемым на основе домена DC при гене- рации начальной популяции. Численное значе-

ние константным символам назначается только при экспрессии генов. Для внесения генетиче- ского разнообразия был добавлен специальный оператор мутации констант. Начальный набор возможных числовых кон- стант может быть задан вручную: как перечис- лением, так и заданием диапазона (успешное решение задач таким методом прямого управ- ления константами возможно только при на- личии априорных знаний о решении, позволя- ющих задать корректный диапазон). Обычно используется метод инициализации значений констант случайными числами.

Динамические константы

В работе [11] предлагается при старте алго- ритма ПЭГ на этапе создания новой популяции начальные значения констант в хромосомах отбирать из множества А ={0,1316, 0,2128, 0,3441, 0,5571, 0,9015, 1,4588, 2,3605, 3,8195, 6,1804, 10,0007}, полученного таким образом, чтобы соотношение соседних элементов было золотым сечением. В данной модификации ис- пользуется следующий оператор мутации каж- дой константы Cj в геноме выбранной особи:  Из фиксированного глобального массива первичных констант А случайным образом вы- бирается константа V.  Случайным образом выбирается оператор Op из множества {+, —, /, *}.  C Op CV jj   , .

Плавная и случайная мутация констант

Исследования операторов мутации, основан- ных на техниках плавной и случайной мутации, описаны в работе [12]. Был задан оператор од- ноточечной мутации константы: при началь- ной конфигурации ПЭГ задается отсортиро- ванный список возможных констант. Этот опе- ратор изменяет одну символ–константу в гене: при случайной мутации на замену выбирается любой другой элемент списка, при плавной – какой-либо из соседних текущему. Данная операция применяется к каждому гену хро- мосомы. Локальный поиск должен проводить- ся в сторону оптимального решения, что означа- ет применение результата мутации только то- гда, когда он повышает значение ФФ особи.

Всего было исследовано пять подходов к мутации:  Плавная мутация лучшей особи в конце расчета поколения.  Случайная мутация лучшей особи в конце расчета поколения.  Плавная мутация каждой особи в первые α процента поколений в конце расчета поколе- ния.  Случайная мутация каждой особи в пер- вые α процента поколений в конце расчета по- коления.  Интервальная случайная мутация: первые g поколений случайной мутации подвергаются все особи популяции в конце расчета поколе- ния. Применение подхода, при котором мутации подвергается только лучшая особь поколения, никак не повлияло на эффективность алгорит- ма. Из этого можно сделать вывод, что лучшая особь, полученная стандартным алгоритмом ПЭГ, по определению достаточно хороша и не требует модификаций. Это подтверждает так- же решающую роль эволюционного процесса ПЭГ (выполнение генетических модификаций и отбор) в поиске оптимальных решений. Применение мутации к каждой особи попу- ляции значительно повышает значение ФФ по- пуляции, особенно в первых поколениях. Од- нако с течением времени процентное соотно- шение особей, улучшенных после мутации, уменьшается. Это происходит вследствие того, что спустя определенное количество поколе- ний формируются группы субоптимальных ре- шений, константы которых уже должным об- разом настроены, поэтому на данном этапе бо- лее значимы операторы, приводящие к боль- шим изменениям. Применение методов, использующих мута- ции констант к каждой особи, приводит к рос- ту времени выполнения алгоритма, однако по- лучение более качественных решений не по- зволяет напрямую сравнить эффективность та- ких модифицированных алгоритмов со стан- дартным ПЭГ. Кроме того, применение упомя- нутых трех техник к различным задачам не по- зволило выявить лучшую из них.

Плавно-динамические константы

Недостаток описанных операторов мутации численных констант это отсутствие тонкой под- стройки коэффициентов особей: степень изме- нения ничем не ограничена и отсутствуют га- рантии поступательного движения в сторону оптимума. Для устранения этого недостатка [13] была построена процедура осуществления направленного процесса эволюции, основанная на комбинации динамического подхода работы с константами ПЭГ и метода иммунных сетей. Создание нового терминала–константы выпол- няется согласно динамическому подходу: но- вому узлу (при создании начальной популяции либо после изменения типа узла на терминал– константу оператором мутации) задается зна- чение одно из элементов массива «золотых се- чений» А. Оператор плавно-динамической му- тации констант изменяет значение в пределах ±10 процентов от текущего: VV random   1 ( 0,1 0,1) .   Результаты эксперимента, подтверждающие преимущество такого подхода в сравнении с не- ограниченной мутацией, приведены в табл. four.

Т а б л и ц а 4. Эффективность алгоритма при плавной и ди- намической мутации констант

Фитнес-функция

Для повышения эффективности отбора в [7, 14] предложено введение порогового значения ФФ. Особи, ФФ которых не достигает этого порогового значения, не допускаются к репро- дукции. Установка порогового значения требует соблюдения баланса между ускорением схо- димости и уменьшением разнообразия, что приводит к преждевременной сходимости. По- этому целесообразно применять динамический порог, обновляющийся на каждой итерации и представляющий собой среднее значение ФФ популяции, умноженное на коэффициент мас- штабирования. В большинстве случаев в зави- симости от задачи используется значение ко- эффициента в диапазоне [0,15; 1,5], с опти-

мальным значением 1,25. Давление на процесс эволюции, оказываемое порогом отбора, по- ложительно влияет на поиск оптимального решения, существенно сокращая время поиска. В схему расчета ФФ в работе [15] добавлен коэффициент давления отбора, отражающий количественную степень влияния возрастания среднеквадратичной ошибки решения на паде- ние его приспособленности f    i, g 1000 / 1 k err(i, g) , где i – индекс особи в популяции; g – поколе- ние; err ig (, ) – среднеквадратичная ошибка i-го решения; k – коэффициент давления отбо- ра; 1000 – максимальное значение ФФ. In fig. 2 приведен график зависимости ФФ от погрешности (MSE) для различных значе- ний k, а в табл. 5 – влияние значения этого ко- эффициента на эффективность модификаций алгоритмов.

Анализ результатов экспериментов по сим-вольной регрессии на различных наборах данн

ых позволил определить оптимальное значе- ние коэффициента давления отбора k = 10,0. Данная величина отличается от значения, при- нятого в исходном алгоритме ПЭГ (k = 100).

Частичный подсчет фитнес-функции

Главным недостатком как эволюционных ал- горитмов в целом, так и ПЭГ в частности есть низкая скорость их работы (в сравнении со ско- ростью построения искусственных нейронных сетей, регрессионных моделей). Любое ускоре- ние алгоритма ПЭГ позволяет улучшить каче-

ство получаемых моделей, так как дает возмож- ность проведения расчета большего количества поколений и выполнения большего числа неза- висимых запусков за эквивалентное время.

Table 5. Efficiency of the algorithm at various pressure coefficients k

It should be noted that the most resource-intensive part of the algorithm is the calculation of the FF, since all available data are fed to the model input, which are then processed in accordance with the program (formula, rule) encoded by the model. In [16], it was possible to obtain a universal method for speeding up the procedure for calculating fitness, which made it possible to significantly improve both performance indicators (eb and rf) and based on the following considerations. The formula for calculating the FF, as a rule, includes the MSE of the model, while the FF value itself serves to compare the efficiency of the models between themselves. As it turned out, such an estimate does not require the calculation of the MSE from the full set of input data. If at a certain stage the current value of the MSE (or the corresponding FF) exceeds a certain threshold, then further calculations can be interrupted. Such an approach makes it possible to avoid unnecessary costs for accurately calculating the PF of poorly adapted individuals, replacing it with an approximate estimated value.

In this case, in order to avoid sequences of adjacent points, the entire set of input data is mixed and divided into G packets k D g: 1, jgj G Data In D    After each packet is processed, the FF is evaluated and based on it the decision to stop computing individuals. The termination condition is a comparison of the FF value for the calculated first K groups with a threshold threshold value, which dynamically changes during the evolution process and therefore is given by a certain fraction (for example, 0.7) of the average FF value of the previous generation: 1 1 (, 1), 0.7 (,) N zjf ig fif ig N          , 1, (,),, jp MSE gj K f iK fi DKG          , where (, 1) fig , (,) fig is the return value of the FF of the ith individual of the calculated and previous generations; (,) zfi threshold is a function of the weighted value of the FF; N is the population size; K - the number of processed groups of input data. To distinguish between individuals whose calculation was interrupted at different points in time (the error threshold value was exceeded when the number of input data groups was different), the penalty coefficient K / G is entered into the formula: (,) (,) (,); (,) (,). zppppfi threshold fi G fi G threshold K fi K fi K threshold G          Thus, bad decisions will use fewer resources, while the best individuals will be calculated most accurately. In tab. 6 shows the results of a comparative analysis of the performance of the original algorithms with modified partial calculation of the standard deviation.

Table 6. Efficiency of an algorithm with various fit functions

Sin rosen sigmas coding scheme FF еb rf еb rf еb rf СКО 0.365 0 0.141 0 0.152 0 1 Part. RMS 0,000 100 0,289 0 0,165 0 R2 14,858 0 4,361 0 0,093 0 RMS 0,000 100 0,275 0 0,138 0 2 Part of RMS 0,000 100 0,285 0 0,165 0 R2 20,775 0 30,153 0 0,765 0 RMS 0,000 100 0,203 0 0,165 0 3 Part. RMS 0,000 100 0,173 0 0,130 0 R2 0,000 100 4,120 0 10608.88 0 Conclusion. In the course of analyzing the existing methods and tools aimed at accelerating the production of the model by the PEG algorithm and increasing its quality, as well as the experiments carried out, a number of limitations of the performance of the traditional algorithm were revealed, such as the duration of the FF calculation, the lack of fine tuning of the numerical constants , the effect of chromosome size on the rate of convergence, problems with finding complex models. Therefore, further research should be aimed at creating methods and approaches to overcome these limitations.