Generation combinatorics of Permutations, placements, combinations with and without repetitions online

This online service offers to generate a given type of combination of elements (permutation, placement or combination)

Enter the quantity m and the elements of the set, listed separated by commas for which you want to generate the specified combinations of elements: m=4;a,b,c,d

generation of permutations P without repetitions for given elements of the set

generation of permutations P with repetitions for given elements of the set

generation of arrangements A (arrangement) without repetitions for given set elements

generation of arrangements A (arrangement) with repetitions for given set elements

generation of C combinations without repetitions for given set elements

generation of C combinations with repetitions for given set elements

generation of permutations P, placements A, combinations C without and with repetitions (simultaneously)

Submit

Reset

Share:

---

Rating 9 of 10. count vote: 234

Are you satisfied?: super great great super great excellent good haven't read or thought about the answer yet not very good medium bad bad Happy very bad terrible

---

Your answer option for this service or noticed an error:

The online service for generating permutations, placements and combinations for given elements of a set is a convenient tool,
which helps users create different combinatorial variations of elements from a given set.
These combinatorial objects are widely used in mathematics, statistics, computer science and other fields.
Brief description of the main functions of our service:
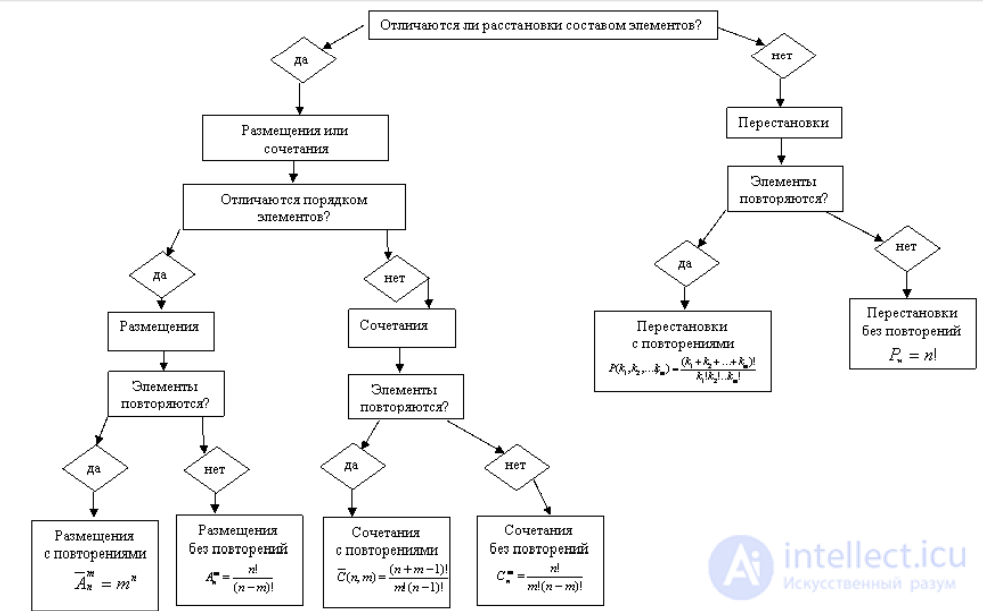
Permutations (P):
Permutations are ordered combinations of elements of a set.
The service allows you to generate all possible permutations of given elements.
You can select many elements and get a list of all their permutations.
Placements (A):
Arrangements are also ordered combinations of elements of a set, but the order of the elements is important here.
The service allows you to create placements of a given size from a variety of elements.
You can specify the placement size and get all possible combinations.
Combinations (C):
Combinations are unordered combinations of elements of a set, where the order does not matter.
The service allows you to generate combinations without repetition, where each element can be used only once,
or combinations with repetitions, where elements may be repeated.
You can specify the size of the combination and select the type: without repetitions or with repetitions.
Additional future features that such a service may provide:
visualization of results: Generated combinations can be displayed in a convenient format that is easy to read and use.
Data export: Possibility to download results in various formats (for example, text files or tables).
Customization options: Ability to select additional parameters such as uniqueness of elements, maximum number of elements and others.
Ability to save history: Saving previously generated combinations for further access or analysis.
Our service is useful for students, researchers, engineers and anyone who works with combinatorial problems
and requires the generation of various combinatorial objects.