The use of neural networks for classification problems. Choosing a coding method for input and output information

The problem of classification is one of the most important applications of neural networks.

The classification task is the task of assigning a sample to one of several mutually disjoint sets. An example of such tasks may be, for example, the problem of determining the creditworthiness of a bank’s client, medical tasks in which it is necessary to determine, for example, the outcome of a disease, the solution of problems of managing a securities portfolio (to buy or buy shares to hold shares depending on the market situation) determining viable and bankrupt firms.

Purpose of classification

When solving classification problems, it is necessary to assign the available static samples (characteristics of the situation on the market, medical examination data, customer information) to certain classes. There are several ways to present data. The most common is the way in which a sample is represented by a vector. The components of this vector are the various characteristics of the sample that influence the decision about which class this sample belongs to. For example, for medical tasks, the data from the patient's medical record may be components of this vector. Thus, on the basis of some information about the example, it is necessary to determine which class it can be attributed to. The classifier thus relates the object to one of the classes in accordance with a certain partitioning of the N-dimensional space, which is called the input space, and the dimension of this space is the number of components of the vector.

First of all, you need to determine the level of complexity of the system. In real-life tasks, a situation often arises when the number of samples is limited, which makes it difficult to determine the complexity of the problem. It is possible to distinguish three main levels of difficulty. The first (the simplest) - when classes can be divided by straight lines (or hyperplanes, if the input space has a dimension greater than two) - the so-called linear separability . In the second case, the classes cannot be separated by lines (planes), but it is possible to separate them using a more complex division — non - linear separability . In the third case, the classes intersect and one can speak only about probabilistic separability .

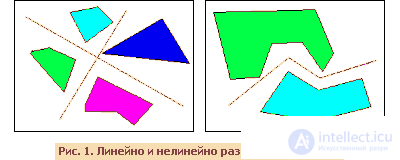
Ideally, after preprocessing, we must obtain a linearly separable problem, since after this the construction of the classifier is greatly simplified. Unfortunately, when solving real problems, we have a limited number of samples, on the basis of which the classifier is built. At the same time, we cannot carry out such preprocessing of data, at which linear separability of samples will be achieved.

Using neural networks as a classifier

Direct link networks are a universal means of approximation of functions, which allows them to be used in solving classification problems. As a rule, neural networks are the most effective way to classify, because they actually generate a large number of regression models (which are used in solving classification problems by statistical methods).

Unfortunately, in the application of neural networks in practical problems, a number of problems arise. First of all, it is not known in advance what complexity (size) a network may need for sufficiently accurate mapping. This complexity may be prohibitively high, which will require a complex network architecture. So Minsky in his work "Perceptrons" proved that the simplest single-layer neural networks are capable of solving only linearly separable tasks. This limitation is surmountable when using multilayer neural networks. In general, we can say that in a network with one hidden layer, the vector corresponding to the input sample is transformed by the hidden layer into some new space, which can have a different dimension, and then the hyperplanes corresponding to the neurons of the output layer divide it into classes. Thus, the network recognizes not only the characteristics of the source data, but also the "characteristics of the characteristics" formed by the hidden layer.

Preparation of source data

To construct a classifier, it is necessary to determine which parameters influence the decision on which class the sample belongs to. There may be two problems. First, if the number of parameters is small, then a situation may arise in which the same set of input data corresponds to examples in different classes. Then it is impossible to train a neural network, and the system will not work correctly (it is impossible to find a minimum that corresponds to such a set of initial data). The source data must be consistent . To solve this problem, it is necessary to increase the dimension of the feature space (the number of components of the input vector corresponding to the sample). But with an increase in the dimension of the feature space, a situation may arise when the number of examples may become insufficient for network training, and instead of generalization, it will simply remember the examples from the training sample and will not be able to function correctly. Thus, in determining the signs, it is necessary to find a compromise with their number.

Next, it is necessary to determine the method of presenting the input data for the neural network, i.e. determine the method of regulation. Normalization is necessary because neural networks work with data represented by numbers in the range 0..1, and the source data can have an arbitrary range or even be non-numeric data. In this case, various methods are possible, ranging from simple linear transformation to the required range and ending with multidimensional analysis of parameters and nonlinear normalization depending on the influence of parameters on each other.

Output encoding

The problem of classification in the presence of two classes can be solved on a network with one neuron in the output layer, which can take one of two values ​​0 or 1, depending on which class the sample belongs to. If there are several classes, there is a problem with the presentation of this data for the network output. The simplest way to represent the output in this case is the vector, the components of which correspond to different class numbers. Moreover, the ith component of the vector corresponds to the ith class. All other components are set to 0. Then, for example, the second class will correspond to 1 to 2 network outputs and 0 to the rest. When interpreting the result, it is usually assumed that the class number is determined by the output number of the network on which the maximum value appears. For example, if in a network with three outputs we have a vector of output values ​​(0.2.0.6.0.4), then we see that the second component of the vector has the maximum value, which means the class to which this example relates is 2. With this encoding method, sometimes The concept of network confidence is also introduced in that example belongs to this class. The easiest way to determine confidence is to determine the difference between the maximum output value and the value of another output that is closest to the maximum. For example, for the example considered above, the network confidence that the example belongs to the second class will be defined as the difference between the second and third component of the vector and is 0.6-0.4 = 0.2. Accordingly, the higher the confidence, the greater the likelihood that the network has given the correct answer. This coding method is the simplest, but not always the most optimal way to present data.

Other methods are known. For example, the output vector is a cluster number written in binary form. Then, if there are 8 classes, we will need a vector of 3 elements, and, say, class 3 will correspond to vector 011. But in this case, if an incorrect value is obtained at one of the outputs, we can get a wrong classification (wrong cluster number), so it makes sense to increase the distance between the two clusters due to the use of the Hamming code coding of the output, which will increase the reliability of the classification.

Another approach is to split the problem with k classes into k * (k-1) / 2 subtasks with two classes (2 by 2 coding) each. The subtask in this case is understood to mean that the network determines the presence of one of the components of the vector. Those. the source vector is divided into groups of two components in each so that they include all possible combinations of the components of the output vector. The number of these groups can be defined as the number of unordered samples of two of the original components. From combinatorics

Ank = k! N! (K − n)! = K! 2! (K − 2)! = K (k − 1) 2

Then, for example, for a problem with four classes, we have 6 outputs (subtasks) distributed as follows:

Where 1 at the output indicates the presence of one of the components. Then we can go to the class number according to the result of the calculation by the network as follows: we determine which combinations received a single (or rather close to one) output value (i.e., which subtasks were activated), and we believe that the class number will be the one that entered the largest number of activated subtasks (see table).

This encoding in many problems gives a better result than the classical encoding method.

Network capacity selection

Choosing the right amount of network is important. It is often simply impossible to build a small and high-quality model, and a large model will simply memorize examples from the training sample and not produce an approximation, which naturally leads to incorrect classifier operation. There are two main approaches to building a network - constructive and destructive. At the first of them, the network of the minimum size is taken first, and gradually increase it until the required accuracy is achieved. At the same time, at every step she is being re-educated. There is also a so-called cascade correlation method, in which, after the epoch ends, the network architecture is adjusted to minimize the error. With a destructive approach, a network of an overestimated volume is first taken, and then nodes and links are removed from it, which have little effect on the solution. It is useful to remember the following rule: the number of examples in the training set must be greater than the number of adjustable weights . Otherwise, instead of generalization, the network will simply remember the data and lose the ability to classify - the result will be undefined for examples that are not included in the training sample.

Network architecture selection

When choosing a network architecture, several configurations with different numbers of elements are usually tested. The main indicator is the volume of the training set and the generalizing ability of the network. A Back Propagation learning algorithm with a confirmation set is usually used.

Algorithm for constructing a classifier based on neural networks

1. Work with data
   • Create a database of examples specific to this problem.
   • Split the entire data set into two sets: training and test (split into 3 sets is possible: training, test and confirming).
2. Preliminary processing
   • Choose a system of features characteristic of the task, and convert the data accordingly to feed the network (normalization, standardization, etc.). As a result, it is desirable to obtain a linearly separable space for multiple samples.
   • Choose a coding system for output values ​​(classical coding, 2 to 2 coding, etc.)
3. Design, training and network quality assessment
   • Select the network topology: the number of layers, the number of neurons in the layers, etc.
   • Select the function of activation of neurons (for example, "sigmoid")
   • Choose a network learning algorithm
   • Evaluate the quality of the network based on the confirmatory set or another criterion, optimize the architecture (reducing weights, thinning the feature space)
   • It will focus on the network variant that provides the best ability to generalize and evaluate the quality of work on the test set
4. Use and diagnosis
   • Find out the degree of influence of various factors on the decision made (heuristic approach).
   • Make sure that the network provides the required classification accuracy (the number of incorrectly recognized examples is small)
   • If necessary, return to step 2, changing the way samples are presented or changing the database.
   • Practically use the network to solve the problem.

In order to build a quality classifier, it is necessary to have quality data. None of the methods for constructing classifiers, based on neural networks or statistical, will never give a qualifier of the desired quality if the existing set of examples is not sufficiently complete and representative of the task that the system will have to work with.