Lecture
The most inquisitive students encounter a characteristic difficulty in the study of physics — a lack of mathematical knowledge. A huge number of interesting problems, the physical content of which is understandable, cannot be solved, since they require knowledge of the derivative, integral or differential equations. For example: students in the 9th grade are introduced to Newton's second law and the law of world wideness, but this is not enough to calculate the movement of the planets and spacecraft. Although the program for physical and mathematical classes provides for the study of the fundamentals of mathematical analysis, however, in secondary school it is hardly possible to master the technique of calculating integrals and solving differential equations to the extent necessary for solving physical problems. And if you have the relevant knowledge, you need to keep in mind that the vast majority of integrals are not calculated through elementary and special functions, and the analytical solution is known only for some classes of differential equations. The ubiquitous distribution of computers makes it possible to solve many problems by numerical methods, based on the replacement of integration by summation and derivatives by finite differences. In this formulation, the tasks become available to the student. The only thing required is a machine that can count.
Computer mathematics systems Maple, Mathematica, Mathlab and Mathcad greatly facilitate the dialogue of the person with the computer when solving mathematical problems. The Mathcad system is distinguished from the above-mentioned systems by an extremely user-friendly interface and excellent graphics. To master Mathcad, unlike the programming languages Pascal, Fortran does not need night vigils for weeks and months. The method of solving a specific problem can be studied right now and immediately applied. You need to remember the minimum amount of information. Writing programs using Mathcad takes much less time than using the mentioned programming languages, due to the large set of built-in functions. All this is important for students from a psychological point of view, since many subjects are accustomed to the fact that true knowledge and skills will not appear immediately, but sometime later, maybe after years of hard work. There is a devaluation of the concept of "now" and everything is postponed to "later." But life is not postponed, it goes, it is what is happening now. In this sense, the Mathcad system increases the price of acquired knowledge, allows them to be applied without delaying the questions of interest indefinitely. Thanks to this, the knowledge gained in the lessons of physics and mathematics becomes a powerful tool for learning about the world around, and not a set of information necessary for solving problems and puzzles at olympiads and entrance exams.
The use of Mathcad in the educational process allows a physics teacher to deeply and clearly highlight many of the issues of the program, and not be limited to the descriptive side of things.
It should also be borne in mind that with traditional teaching methods, students, although they gain useful knowledge, have a very vague idea about the content and methods of science. Very often, having mastered the task of solving an inclined plane, lenses, electrical circuits with batteries and light bulbs, etc., the student thinks that this is physics. In this sense, the traditional methods of teaching to some extent disorient the student. The use of computer mathematics systems is typical for the work of a scientist, therefore the use of Mathcad in the educational process contributes to the professional orientation of students who are thinking of a career as a scientist.
In the gymnasium there are two computer classes equipped with modern computers, and besides, the overwhelming majority of the students of the physical education class have computers at home. This is the material basis for the implementation of the Mathcad system in the educational process. The curriculum in the Physics and Mathematics class provides for the study of the basics of Mathcad in the 10th grade in the first quarter for 16 hours and the constant use of the Mathcad throughout the 10th and 11th grades. The introductory course ends with a test in which students must demonstrate the ability to:
The last point is of particular importance because it is the basis of numerical integration.
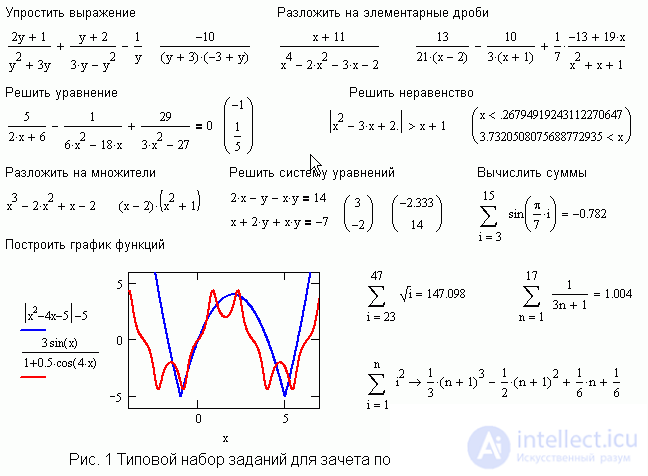
A typical version of the assignments for the test is presented in Fig. 1. Later, students apply their knowledge to perform homework in mathematics and physics, and also explore other possibilities of Mathcad as they progress through relevant material in the lessons of mathematics, physics and computer science. This means differentiation and integration, the solution of differential equations, the construction of three-dimensional graphs and three-dimensional figures, programming in the Mathcad system.
Starting from the second quarter, in the 10th grade, students do their homework in physics at least once a week using the Mathcad system. Completed tasks once a week are presented to the teacher on floppy disks, or sent by e-mail. Part of the tests in physics at the end of the 10th grade and the first half of the 11th grade is the solution of physical problems with the help of the Mathcad system.
For students of the 9th grade, students who wish to continue their studies in a physical mathematics class, during the year, once a week, classes were conducted on solving physical problems using the Mathcad system. At these extra-curricular activities, students mastered the Mathcad system at the level of the above set-off requirements and programming, as well as familiarized themselves with the graphic editor CorelDRAW, which is necessary for the quality of homework. Most of the time it took to solve problems, mainly in mechanics (numerical integration of the equations of motion).
In our opinion, a better understanding of the possibilities of using Mathcad in high school conditions can provide a set of problems solved by students. A review of the tasks and comments to them will form the basis for further discussion. It is assumed that the well-known qualification of acquainting with these lines eliminates the need to provide detailed conditions and problem solving. It should be noted that a number of noteworthy topics are not reflected in this material due to lack of space or technical capabilities, for example: using animation to model wave processes, the motion of celestial bodies in a field of double stars, a solar sail, three-dimensional modeling of potential, movement in a magnetic field etc.
Samples of tasks offered to students are aimed at demonstrating with a specific example the diversity of Mathcad’s mathematical tools, and the choice of physical topics is arbitrary in the sense that although there are many interesting tasks for all sections of the physics course, the physics course program is completely reflected. does not have.
Calculate the mean square velocity of molecules using the user function.
The most appropriate way to solve the problem is to create a user function. The formula uses the absolute temperature, and in the condition of the temperature given in degrees Celsius, in addition, it is necessary to calculate the mass of the molecule. It is not necessary to calculate the absolute temperature and calculate the mass of molecules separately, but it is enough to substitute formulas with numbers instead of arguments into the user function. The solution of the problem by means of Mathcad is shown in fig. 2

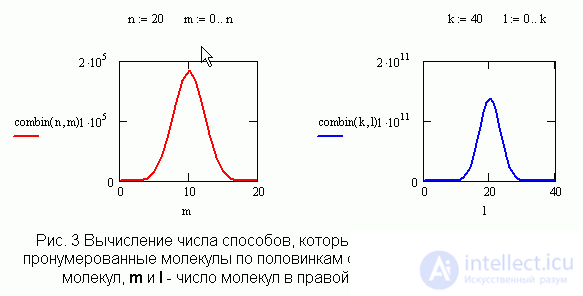
Methods of distribution of molecules in halves of the vessel.
To illustrate the concept of the most probable state when studying the second law of thermodynamics, consider a vessel in which numbered molecules are located and count the number of ways in which one or another situation is realized. Quickly and not less clearly, the result can be obtained by means of Mathcad fig. 3. The graphs give an idea that the most likely situation corresponds to a uniform distribution of molecules. And the number of ways in which uniform distribution is realized gives an idea of the probability of deviation from the equilibrium state if the number of molecules is equal to the number of Loshmidt.
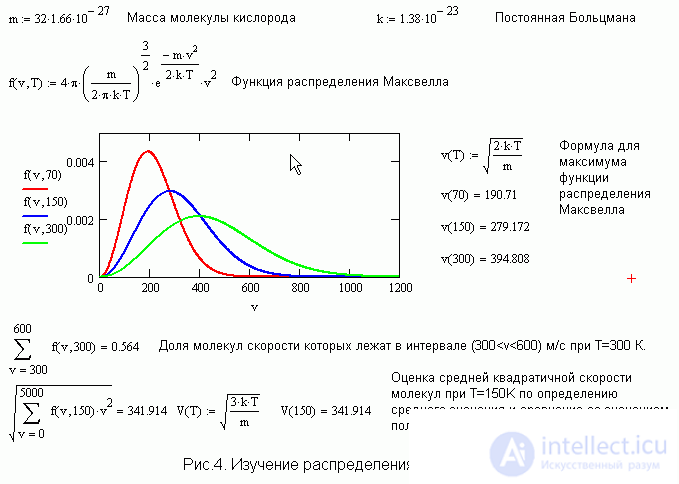
Maxwell distribution.
Fig. 4 gives an idea of the quality of the study of this topic, if the student has Mathcad at his disposal. You can study the effect of temperature on the shape and height of the curve, as well as on the position of the maximum of the distribution function. With the help of summation, it is possible to calculate the fraction of molecules possessing velocities in any interval, as well as to determine the average and mean square velocities of molecules by simple summation.
Brownian motion.
The presence of a random number generator makes it possible to model the motion of a Brownian particle. Fig. 5 gives an idea of how quickly and easily you can get the desired result.

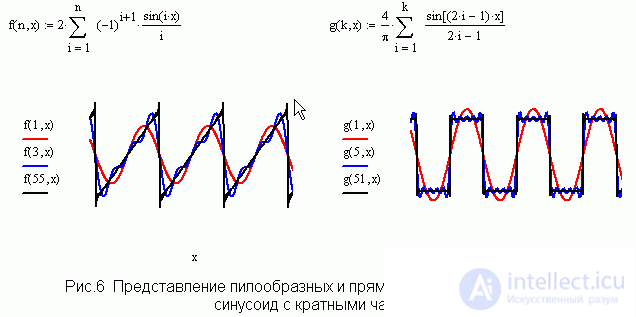
Harmonic analysis.
When telling students about the timbre of the sound, they say that the presence of overtones determines the color of the sound. They also add that overtones are vibrations with frequencies multiple to the main one. But how to get a non-sinusoidal oscillation using a set of harmonics, students can only guess. Fig. 6 shows how this problem is solved with the help of Mathcad. It is quite clearly seen that by adding in a certain proportion the harmonics with multiple frequencies, one can get oscillations of the desired shape, and the greater the number of harmonics, the more clearly the shape of the desired oscillation appears. After the meaning of harmonic analysis is clearly understood at a qualitative level, formulas for Fourier series coefficients can be communicated to the most inquisitive students. With the help of Mathcad, the student can calculate the necessary integrals.
Simulation of oscillations of a mathematical pendulum.
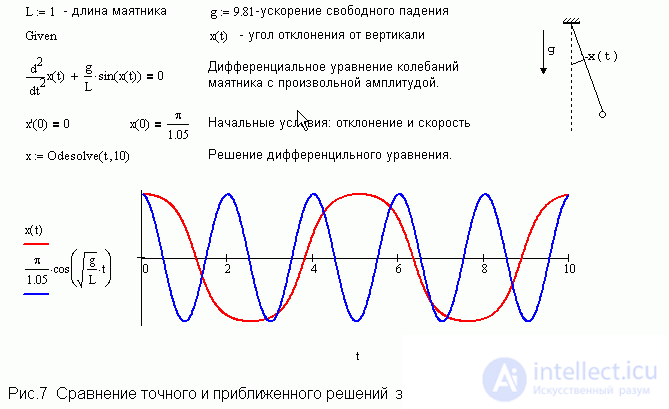
When deriving a formula for the oscillation period of a mathematical pendulum, it is noted that this formula is valid for small oscillation amplitudes. And what will happen with large amplitudes of oscillations? Mathcad allows you to comprehensively explore the problem. One can numerically obtain solutions of the exact and approximate differential equations of oscillations of a mathematical pendulum, and then compare the results obtained. In the case of small amplitudes, the agreement between the approximate and exact solutions is really good, the graphs of both solutions are superimposed on each other over several periods. And in the case of large amplitudes, as Figure 7 shows, the discrepancy is both quantitative and qualitative. At large amplitudes, the oscillations are clearly not sinusoidal. Thus, the student not only gets an idea of the accuracy of an approximate formula, but can get a result for arbitrary amplitudes.
Application of the principle of superposition to calculate the forces of electrostatic interaction in the case of a large number of charges.
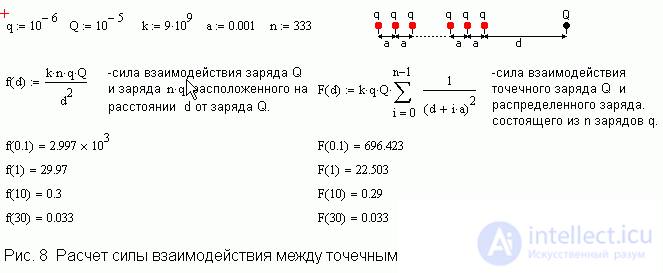
In a school course, electrostatics are limited to studying the interaction of point charges, and the solution of the issues of calculating the interaction of charged bodies is not mentioned, although from an ideological point of view the task is quite simple: you need to break the body into small parts and apply the principle of superposition. Of course, this method is possible in the presence of appropriate computational tools. Fig. 8 and 9 show the solution of two electrostatic problems by means of Mathcad. These tasks can serve as an intermediate step on the way to mastering methods for solving problems with an arbitrary charge distribution. It is very useful to compare the results with those obtained by applying the Coulomb law, if the group of charges were in one point, at a distance x from the selected charge. At large distances x from the system, the results, as expected, are close. Thus, we get an illustration of the criterion of charge accuracy: charges can be considered point, if the distance between the interacting charges is large compared to the size of the charges. After solving these problems, one can easily calculate the interaction forces between a charged rod and a point charge. The solution of such problems gives good material for studying later the concept of an integral.

Calculation of the electrical circuit using the Kirchhoff rules.
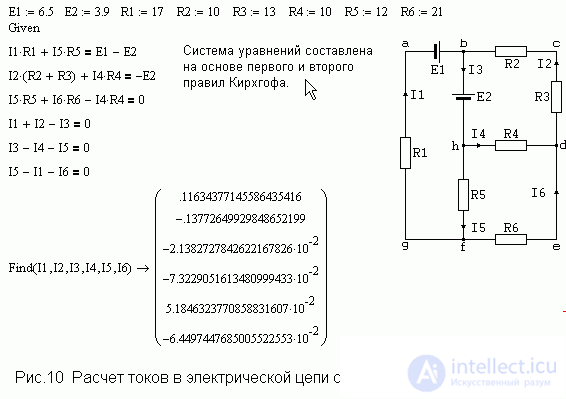
The use of Mathcad is very effective in solving problems where it is necessary to use systems of linear equations, for example, the calculation of electrical circuits. Although from a mathematical point of view, the task is simple, however, a large amount of computational work makes the problem in the case of, for example, 10 equations technically impracticable due to almost inevitable errors. You can write a system of 10 equations, but you can solve it ... Using the built-in Mathcad function, you can easily cope with this task. Fig. 10 illustrates the amount of work needed to solve problems of this type.
Nonlinear elements in the electrical circuit.
Superficial knowledge of the school curriculum creates the illusion that the most important law of electromagnetism is Ohm’s law. His place in the school course is determined by the fact that it is expressed by a simple formula. Meanwhile, the linear relationship between current and voltage is the exception rather than the rule, and the most interesting and fruitful uses of electricity begin where Ohm’s law is violated. As an example of the application of Mathcad, we consider the problem of the series connection of an ohmic resistance and a nonlinear element whose current – voltage characteristic is described by a power function (a power current – voltage characteristic is characteristic of a varistor). From a mathematical point of view, the difficulty of this task is connected with the need to solve an equation in which the unknown can be in a non-integer degree greater than two. Mathcad allows you to easily solve the equation numerically and determine the voltage on the circuit elements, and also to plot the voltage dependence of the nonlinear element U on the external voltage E. Figure. 11 shows how non-linearity can be studied by means of Mathcad. The resulting graph suggests that the nonlinear element stabilizes the voltage, i.e. if E changes 5 times, then voltage U changes 3 times.

The problem of charges on the threads.
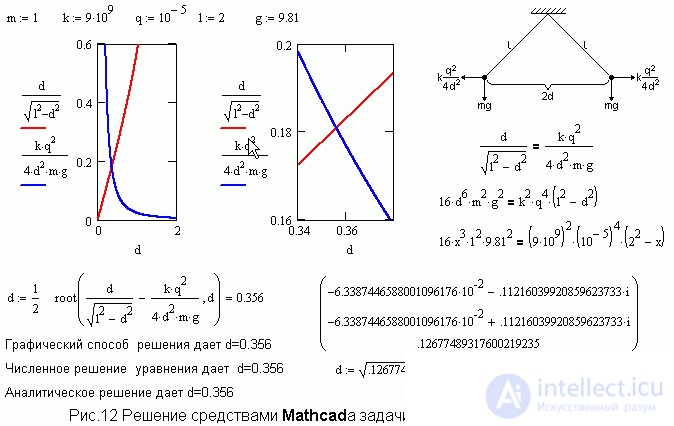
Many generations of students solved the problem of repulsive charged balls suspended on strings. The angle between the threads and the length of the threads are set and you need to find either the amount of charge or the mass of the ball. However, if you modify the formulation of the problem and assume that the angle between the threads or the distance between the balls is unknown, and the mass and charge of the balls, as well as the length of the thread, are known, the problem becomes insoluble for the student due to the cubic equation. With the help of Mathcad, the equation can be solved either analytically, either numerically or graphically. Different solutions to this problem are presented in Fig. 12.
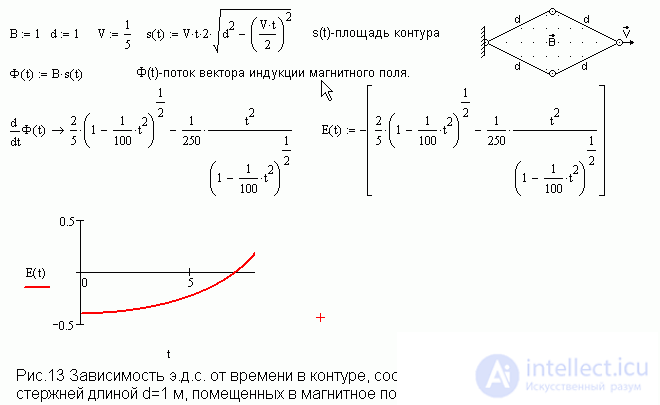
E. D.S. in a deformable contour placed in a magnetic field.
Figure 13 presents an example of using Mathcad for finding the derivative and plotting the dependence of e. d. contour from time to time. It is clear that the task can be complicated by setting an arbitrary dependence on time and a changing magnetic field, however, in this case too, the amount of work increases slightly. From this example, it can be seen that electromagnetic induction problems can be infinitely varied, and not limited to screech marks by changing the area of a rectangular contour and by a frame and a rod evenly rotating in a magnetic field.
The effect of compressibility of water on the depth of the world's oceans.
Due to the extremely important summation, we present one more problem on this topic. The average depth of the World Ocean is 4000 m. Although students often hear about the low compressibility of water, we calculate (estimate) how the sea level would change if the compressibility of water was zero. We divide the water column into layers (height, for example, 1 meter) and calculate the change in the height of each layer due to the pressure of the overlying layers. The solution of the problem is presented in fig. 14. The results of the decision show that the compressibility of water has a significant effect on the land area.

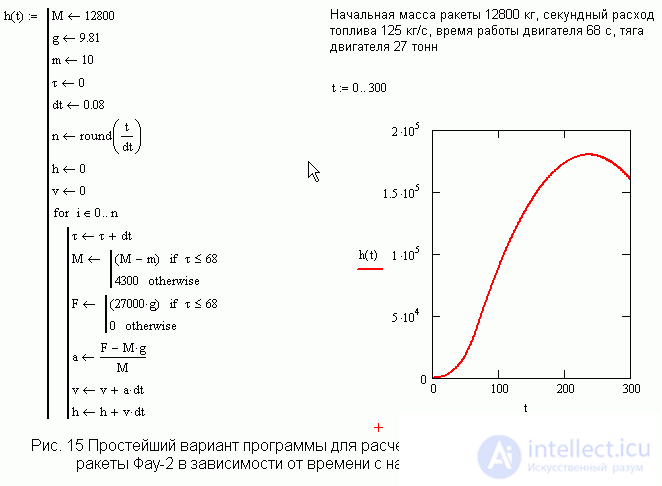
Flight simulation of V-2 rocket.
Infinite possibilities for creating new tasks gives programming. Mathcade has everything you need to write elegant programs. В литературе есть подробные данные о ракете Фау-2, что позволяет моделировать полет ракеты и сравнить с параметрами реального полета. Даже столь простая программа, как представлена на рис. 15, довольно точно отражает полет настоящей ракеты. Компьютер позволяет, не ломая голову над дифференциальными уравнениями описывающих движение переменной массы, на основе простейших знаний, которыми располагает учащийся 9-го класса, исследовать полет реальной ракеты. Надо ли говорить, что без компьютера возможно лишь качественное описание реактивного движения как иллюстрации закона сохранения импульса.
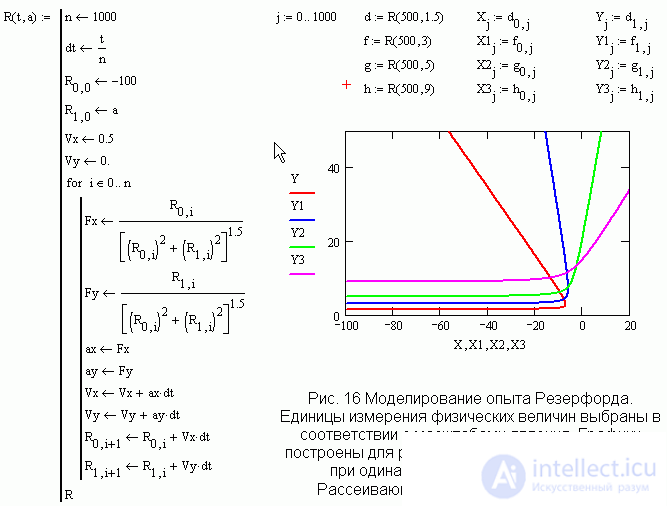
Моделирование опытов Резерфорда.
Гораздо глубже можно понять значение открытия Резерфорда, если на основании уравнений движения построить модель движения альфа частицы в поле ядра. Только с помощью расчета можно убедится, что большие отклонения альфа частицы могут случаться только в том случае, если заряд сконцентрирован в очень маленькой области с размерами порядка нескольких ферми. Томсоновская модель атома ни при каких условиях не может дать больших отклонений. Все это можно получить только на основе расчета, любые качественные аргументы здесь бессильны. На рис.16 представлена программа и результаты расчетов движения альфа частиц. В формулах используются единицы измерения, характерные для масштабов изучаемого явления.
В связи с повсеместным распространением компьютеров и появлением систем компьютерной математики, в частности Mathcadа, можно и нужно существенно изменить характер и уровень преподавания школьных курсов физики и математики. Целесообразность широкого применения Mathcadа можно мотивировать следующим образом:
С учетом вышеизложенного представляется необходимой разработка новых задач, по крайней мере, для учащихся физматклассов и физматшкол. Представленный материал можно рассматривать как идею создания сборника задач по физике для физматшкол, изложенную на предметном уровне.
Comments
To leave a comment
applied Physics
Terms: applied Physics